Contents
【問題】
【難易度】★★★★☆(やや難しい)
単相\( \ 2 \ \)線式配電線があり,この末端に\( \ 300 \ \mathrm {[kW]} \ \)の需要家がある。
この配電線の途中,図に示す位置に\( \ 6 \ 300 \ \mathrm {[V]} / 6 \ 900 \ \mathrm {[V]} \ \)の昇圧器を設置して受電端電圧を\( \ 6 \ 600 \ \mathrm {[V]} \ \)に保つとき,次の(a)及び(b)の問に答えよ。
ただし,配電線の\( \ 1 \ \)線当たりの抵抗は\( \ 1 \ \mathrm {[\Omega / km ]} \ \),リアクタンスは\( \ 1.5 \ \mathrm {[\Omega / km ]} \ \)とし,昇圧器のインピーダンスは無視するものとする。

(a) 末端の需要家が力率\( \ 1 \ \)の場合,受電端電圧を\( \ 6 \ 600 \ \mathrm {[V]} \ \)に保つとき,昇圧器の二次側の電圧\( \ V_{2} \ \mathrm {[V]} \ \)の値として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 6 \ 691 \ \) (2) \( \ 6 \ 757 \ \) (3) \( \ 6 \ 784 \ \) (4) \( \ 6 \ 873 \ \) (5) \( \ 7 \ 055 \ \)
(b) 末端の需要家が遅れ力率\( \ 0.8 \ \)の場合,受電端電圧を\( \ 6 \ 600 \ \mathrm {[V]} \ \)に保つとき,送電端の電圧\( \ V_{\mathrm {s}} \ \mathrm {[V]} \ \)の値として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 6 \ 491 \ \) (2) \( \ 6 \ 519 \ \) (3) \( \ 6 \ 880 \ \) (4) \( \ 7 \ 016 \ \) (5) \( \ 7 \ 189 \ \)
【ワンポイント解説】
配電線の電圧降下に関する問題です。
昇圧器がなければよく出題される問題パターンと思いますが,昇圧器が絡むことで計算量が多くなり少し難易度を上げている問題と言えます。
(a)が解ければ合格圏内には入っていると考えて良いと思います。
1.配電線の電圧降下の近似式
①単相\( \ 2 \ \)線式送電線の電圧降下
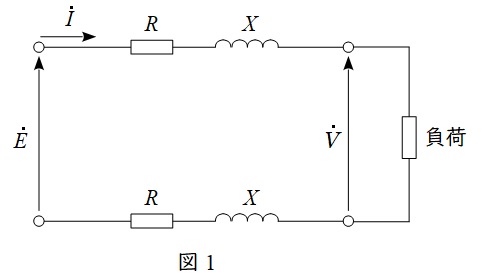
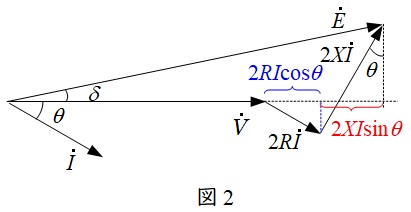
単相\( \ 2 \ \)線式線路は図1のような回路になり,負荷に対して供給される線路と戻りの線路の\( \ 2 \ \)段階で電圧降下が発生します。したがって,負荷の力率が遅れ力率\( \ \cos \theta \ \)であるときのベクトル図を描くと図2のようになります。
図2のベクトル図において,\( \ \dot E \ \)と\( \ \dot V \ \)の位相差が十分に小さいと仮定すると,線路の電圧降下\( \ \varepsilon =E-V \ \)は,
\[
\begin{eqnarray}
E&≃&V+2RI\cos \theta +2XI\sin \theta \\[ 5pt ]
E-V&=&2RI\cos \theta +2XI\sin \theta \\[ 5pt ]
\varepsilon &=&2I\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ]
\end{eqnarray}
\]
と求められます。
②三相\( \ 3 \ \)線式送電線の電圧降下
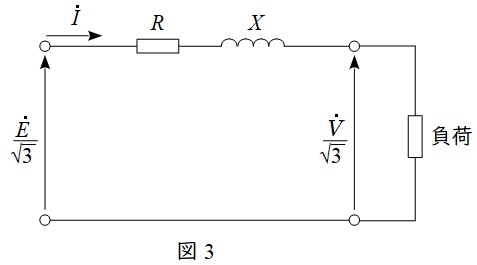
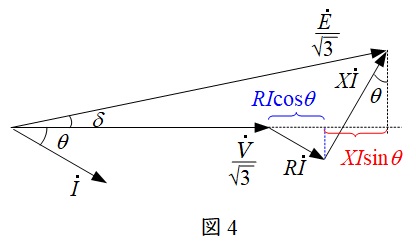
三相回路においては,一相分の等価回路及びベクトル図は図3及び図4のように描くことができ,三相分の電圧降下\( \ \varepsilon \ \)は,
\[
\begin{eqnarray}
\frac {E}{\sqrt {3}}&≃&\frac {V}{\sqrt {3}}+RI\cos \theta +XI\sin \theta \\[ 5pt ]
\frac {E}{\sqrt {3}}-\frac {V}{\sqrt {3}}&=&RI\cos \theta +XI\sin \theta \\[ 5pt ]
E-V&=&\sqrt {3}\left( RI\cos \theta +XI\sin \theta \right) \\[ 5pt ]
\varepsilon &=&\sqrt {3}I\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ]
\end{eqnarray}
\]
と求められます。
2.変圧器の巻数比と変圧比,変流比の関係
変圧器の一次側の巻数\( \ N_{1} \ \),電圧\( \ V_{1} \ \mathrm {[V]} \ \),電流\( \ I_{1} \ \mathrm {[A]} \ \),二次側の巻数\( \ N_{2} \ \),電圧\( \ V_{2} \ \mathrm {[V]} \ \),電流\( \ I_{2} \ \mathrm {[A]} \ \)とすると,それぞれの関係は,
\[
\begin{eqnarray}
\frac {N_{1}}{N_{2}} &=&\frac {V_{1}}{V_{2}}=\frac {I_{2}}{I_{1}} \\[ 5pt ]
\end{eqnarray}
\]
となります。インピーダンスは電圧を電流で割ったものであるため,一次側換算のインピーダンス\( \ Z_{1} \ \mathrm {[\Omega ]} \ \),二次側換算のインピーダンス\( \ Z_{2} \ \mathrm {[\Omega ]} \ \)とすると,
\[
\begin{eqnarray}
\frac {Z_{1}}{Z_{2}} &=&\frac {\displaystyle \frac {V_{1}}{I_{1}}}{\displaystyle \frac {V_{2}}{I_{2}}} \\[ 5pt ]
&=&\frac {V_{1}}{I_{1}}\times \frac {I_{2}}{V_{2}} \\[ 5pt ]
&=&\frac {V_{1}}{V_{2}}\times \frac {I_{2}}{I_{1}} \\[ 5pt ]
&=&\left( \frac {N_{1}}{N_{2}} \right) ^{2} \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。
【解答】
(a)解答:(3)
需要家の電力が\( \ P_{\mathrm {L}}=300 \ \mathrm {[kW]} \ \),受電端電圧が\( \ V_{\mathrm {r}}=6 \ 600 \ \mathrm {[V]} \ \)であるから,需要家に供給される電流\( \ I_{\mathrm {2}} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {2}}&=&\frac {P_{\mathrm {L}}}{V_{\mathrm {r}}} \\[ 5pt ]
&=&\frac {300 \times 10^{3}}{6 \ 600} \\[ 5pt ]
&≒&45.45 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となる。また,昇圧器から受電端までの抵抗\( \ R_{2} \ \mathrm {[\Omega ]} \ \)及びリアクタンス\( \ X_{2} \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
R_{\mathrm {2}}&=&2\times 1 \\[ 5pt ]
&=&2 \ \mathrm {[\Omega ]} \\[ 5pt ]
X_{\mathrm {2}}&=&2\times 1.5 \\[ 5pt ]
&=&3 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
である。ワンポイント解説「1.配電線の電圧降下の近似式」の通り,昇圧器の二次側の電圧\( \ V_{2} \ \mathrm {[V]} \ \)は,力率が\( \ \cos \theta =1 \ \)であることに注意すると,
\[
\begin{eqnarray}
V_{\mathrm {2}}&=&V_{\mathrm {r}}+2I_{2}\left( R_{2}\cos \theta +X_{2}\sin \theta \right)\\[ 5pt ]
&=&V_{\mathrm {r}}+2I_{2}R_{2} \\[ 5pt ]
&=&6600+2\times 45.45\times 2 \\[ 5pt ]
&≒&6 \ 782 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(b)解答:(4)
需要家の電力が\( \ P_{\mathrm {L}}=300 \ \mathrm {[kW]} \ \),受電端電圧が\( \ V_{\mathrm {r}}=6 \ 600 \ \mathrm {[V]} \ \)であり,力率が\( \ \cos \theta =0.8 \ \)であるから,需要家に供給される電流\( \ I_{\mathrm {2}} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {L}}&=&V_{\mathrm {r}}I_{\mathrm {2}}\cos \theta \\[ 5pt ]
I_{\mathrm {2}}&=&\frac {P_{\mathrm {L}}}{V_{\mathrm {r}}\cos \theta } \\[ 5pt ]
&=&\frac {300 \times 10^{3}}{6 \ 600\times 0.8} \\[ 5pt ]
&≒&56.82 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となる。
送電端から昇圧器までの抵抗\( \ R_{1} \ \mathrm {[\Omega ]} \ \)及びリアクタンス\( \ X_{1} \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
R_{\mathrm {1}}&=&3\times 1 \\[ 5pt ]
&=&3 \ \mathrm {[\Omega ]} \\[ 5pt ]
X_{\mathrm {1}}&=&3\times 1.5 \\[ 5pt ]
&=&4.5 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
であり,二次側に換算した値\( \ R_{\mathrm {1}}^{\prime } \ \mathrm {[\Omega ]} \ \)及び\( \ X_{1}^{\prime } \ \mathrm {[\Omega ]} \ \)は,ワンポイント解説「2.変圧器の巻数比と変圧比,変流比の関係」の通り,
\[
\begin{eqnarray}
R_{\mathrm {1}}^{\prime }&=&\left( \frac {N_{2}}{N_{1}}\right) ^{2}R_{\mathrm {1}} \\[ 5pt ]
&=&\left( \frac {V_{2}}{V_{1}}\right) ^{2}R_{\mathrm {1}} \\[ 5pt ]
&=&\left( \frac {6 \ 900}{6 \ 300}\right) ^{2}\times 3 \\[ 5pt ]
&≒&3.599 \ \mathrm {[\Omega ]} \\[ 5pt ]
X_{\mathrm {1}}^{\prime }&=&\left( \frac {N_{2}}{N_{1}}\right) ^{2}X_{\mathrm {1}} \\[ 5pt ]
&=&\left( \frac {V_{2}}{V_{1}}\right) ^{2}X_{\mathrm {1}} \\[ 5pt ]
&=&\left( \frac {6 \ 900}{6 \ 300}\right) ^{2}\times 4.5 \\[ 5pt ]
&≒&5.398 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,二次側に換算した送電端電圧\( \ V_{\mathrm {s}}^{\prime } \ \mathrm {[V]} \ \)は,ワンポイント解説「1.配電線の電圧降下の近似式」の通り,
\[
\begin{eqnarray}
V_{\mathrm {s}}^{\prime }&=&V_{\mathrm {r}}+2I_{2}\left\{ \left( R_{\mathrm {1}}^{\prime }+R_{\mathrm {2}}\right) \cos \theta +\left( X_{\mathrm {1}}^{\prime }+X_{\mathrm {2}}\right) \sin \theta \right\} \\[ 5pt ]
&=&V_{\mathrm {r}}+2I_{2}\left\{ \left( R_{\mathrm {1}}^{\prime }+R_{\mathrm {2}}\right) \cos \theta +\left( X_{\mathrm {1}}^{\prime }+X_{\mathrm {2}}\right) \sqrt {1-\cos ^{2}\theta } \right\} \\[ 5pt ]
&=&6 \ 600+2\times 56.82\times \left\{ \left( 3.599+2\right) \times 0.8 +\left( 5.398+3\right) \times \sqrt {1-0.8 ^{2} } \right\} \\[ 5pt ]
&≒&6 \ 600+113.6\times \left\{ 5.599 \times 0.8 + 8.398 \times 0.6 \right\} \\[ 5pt ]
&≒&7 \ 681 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,求める送電端電圧\( \ V_{\mathrm {s}} \ \mathrm {[V]} \ \)は,一次側換算すると,
\[
\begin{eqnarray}
V_{\mathrm {s}}&=&\frac {6 \ 300}{6 \ 900}\times V_{\mathrm {s}}^{\prime } \\[ 5pt ]
&=&\frac {6 \ 300}{6 \ 900}\times 7 \ 681 \\[ 5pt ]
&≒&7 \ 013 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは