《機械》〈回転機〉[H23:問4]同期発電機の出力端子間電圧に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

次の文章は，同期発電機に関する記述である。

\( \ \mathrm {Y} \ \)結線の非突極形三相同期発電機があり，各相の同期リアクタンスが\( \ 3 \ \mathrm {[\Omega ]} \ \)，無負荷時の出力端子と中性点間の電圧が\( \ 424.2 \ \mathrm {[V]} \ \)である。この発電機に\( \ 1 \ \)相当たり\( \ R+\mathrm {j}X_{\mathrm {L}} \ \mathrm {[\Omega ]} \ \)の三相平衡\( \ \mathrm {Y} \ \)結線の負荷を接続したところ各相に\( \ 50 \ \mathrm {[A]} \ \)の電流が流れた。接続した負荷は誘導性でそのリアクタンス分は\( \ 3 \ \mathrm {[\Omega ]} \ \)である。ただし，励磁の強さは一定で変化しないものとし，電機子巻線抵抗は無視するものとする。

このときの発電機の出力端子間電圧\( \ \mathrm {[V]} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 300 \ \)　　(2)　\( \ 335 \ \)　　(3)　\( \ 475 \ \)　　(4)　\( \ 581 \ \)　　(5)　\( \ 735 \ \)

【ワンポイント解説】

同期発電機における端子電圧の導出に関する問題です。
考え方としてはそれほど難しい内容はありませんが，三平方の定理を多く利用した問題なので，計算力がポイントとなりそうな問題です。

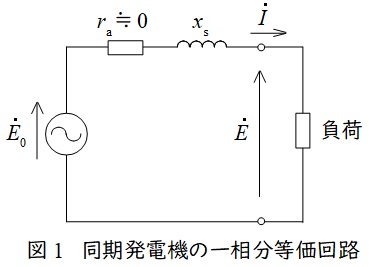
1.同期発電機の等価回路
同期発電機の一相分等価回路は誘導起電力（相電圧）\( \ {\dot E}_{0} \ \mathrm {[V]} \ \)，端子電圧（相電圧）\( \ \dot E \ \mathrm {[V]} \ \)，同期リアクタンス\( \ x_{\mathrm {s}} \ \mathrm {[\Omega ]} \ \)，電機子巻線抵抗\( \ r_{\mathrm {a}} \ \mathrm {[\Omega ]} \ \)とすると，図1のようになります。
通常，電機子巻線抵抗\( \ r_{\mathrm {a}} \ \mathrm {[\Omega ]} \ \)は十分に小さいと考え，無視して考えることが一般的です。

【解答】

解答：(4)
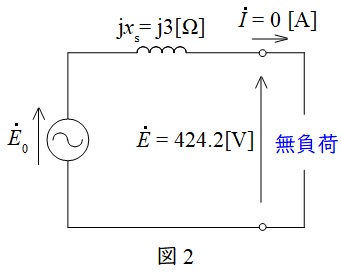
無負荷時の等価回路を図2に示す。ただし，誘導起電力（相電圧）を\( \ {\dot E}_{0} \ \mathrm {[V]} \ \)，端子電圧（相電圧）を\( \ \dot E \ \mathrm {[V]} \ \)，同期リアクタンスを\( \ x_{\mathrm {s}} \ \mathrm {[\Omega ]} \ \)とする。
図2より回路に電流が流れないので，誘導起電力\( \ E_{0} \ \)も\( \ 424.2 \ \mathrm {[V]} \ \)となる。

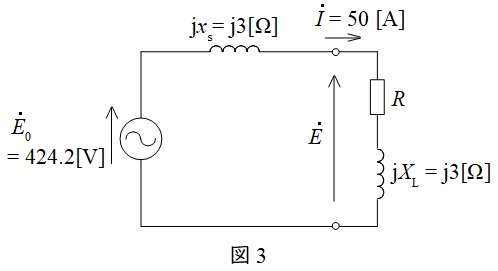
次に\( \ R+\mathrm {j}X_{\mathrm {L}} \ \mathrm {[\Omega ]} \ \)の三相平衡負荷を接続したときの等価回路を図3に示す。
図3より，全体のインピーダンス\( \ \dot Z \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
\dot Z &=& \mathrm {j}x_{\mathrm {s}}+R+\mathrm {j}X_{\mathrm {L}} \\[ 5pt ] &=& \mathrm {j}3+R+\mathrm {j}3 \\[ 5pt ] &=& R+\mathrm {j}6 \\[ 5pt ] \end{eqnarray}
\] であり，その大きさ\( \ Z \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
Z &=&\sqrt {R^{2}+6^{2}} \\[ 5pt ] &=& \sqrt {R^{2}+36} \\[ 5pt ] \end{eqnarray}
\] である。また，誘導起電力（相電圧）\( \ E_{0}=424.2 \ \mathrm {[V]} \ \)，電機子電流\( \ I=50 \ \mathrm {[A]} \ \)より，
\[
\begin{eqnarray}
Z &=&\frac {E_{0}}{I} \\[ 5pt ] &=& 8.484 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となるので，
\[
\begin{eqnarray}
\sqrt {R^{2}+36} &=&8.484 \\[ 5pt ] R^{2}+36&≒& 71.98 \\[ 5pt ] R^{2}&=& 35.98 \\[ 5pt ] R&≒& 5.998 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。したがって，発電機端子電圧（相電圧）\( \ E \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
E &=&\sqrt {R^{2}+X_{\mathrm {L}}^{2}}\times I \\[ 5pt ] &=&\sqrt {5.998^{2}+3^{2}}\times 50 \\[ 5pt ] &≒& 335.3 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となり，線間電圧\( \ V \ \mathrm {[V]} \ \)は相電圧\( \ E \ \mathrm {[V]} \ \)の\( \ \sqrt {3} \ \)倍なので，
\[
\begin{eqnarray}
V &=&\sqrt {3}E \\[ 5pt ] &=&\sqrt {3}\times 335.3 \\[ 5pt ] &≒& 581 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。