《機械》〈回転機〉[R2:問2]界磁に永久磁石を用いた小形直流発電機の効率に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

界磁に永久磁石を用いた小形直流発電機がある。回転軸が回らないよう固定し，電機子に\( \ 3 \ \mathrm {V} \ \)の電圧を加えると，定格電流と同じ\( \ 1 \ \mathrm {A} \ \)の電機子電流が流れた。次に，電機子回路を開放した状態で，回転子を定格回転数で駆動すると，電機子に\( \ 15 \ \mathrm {V} \ \)の電圧が発生した。この小形直流発電機の定格運転時の効率の値\( \ \mathrm {[％]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし，ブラシの接触による電圧降下及び電機子反作用は無視できるものとし，損失は電機子巻線の銅損しか存在しないものとする。

　(1)　\( \ 70 \ \)　　(2)　\( \ 75 \ \)　　(3)　\( \ 80 \ \)　　(4)　\( \ 85 \ \)　　(5)　\( \ 90 \ \)

【ワンポイント解説】

直流発電機の計算問題です。永久磁石ということは，界磁が一定であり，等価回路としては他励発電機の電機子巻線のみを考えれば良いということになります。

1.直流他励発電機の電機子回路の等価回路
図1に直流他励発電機の電機子回路の等価回路を示します。図1において，\( \ V \ \)は端子電圧，\( \ E \ \)は誘導起電力，\( \ I_{\mathrm {a}} \ \)は電機子電流，\( \ R_{\mathrm {a}} \ \)は電機子抵抗となります。

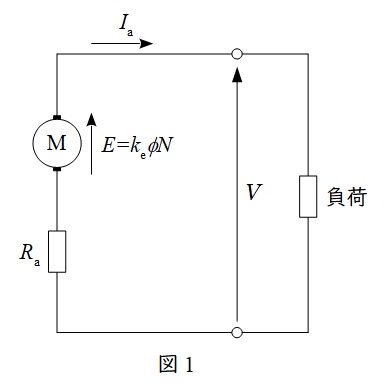
また，上記の等価回路にキルヒホッフの法則を適用すると，以下の関係式が導き出せることが分かります。
\[
\begin{eqnarray}
E &=& V+R_{\mathrm {a}}I_{\mathrm {a}} \\[ 5pt ] \end{eqnarray}
\]

2.直流機の誘導起電力\( \ E \ \)
磁極の数\( \ p \ \)，電機子導体数\( \ Z \ \)，電機子巻線並列回路数\( \ a \ \)，各極の磁束\( \ \phi \ \)，回転速度\( \ N \ \)とすると，直流機の誘導起電力\( \ E \ \)は，
\[
\begin{eqnarray}
E &=&\frac {pZ}{60a}\phi N \\[ 5pt ] &=&k_{\mathrm {e}}\phi N \\[ 5pt ] \end{eqnarray}
\] となり，磁束\( \ \phi \ \)と回転速度\( \ N \ \)に比例します。

3.直流発電機の効率\( \ \eta \ \)
直流発電機の端子電圧が\( \ V \ \)，誘導起電力が\( \ E \ \)，電機子電流が\( \ I_{\mathrm {a}} \ \)であるとき，発電機の入力\( \ P_{\mathrm {i}} \ \)及び出力\( \ P_{\mathrm {o}} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {i}} &=&EI_{\mathrm {a}} \\[ 5pt ] P_{\mathrm {o}} &=&VI_{\mathrm {a}} \\[ 5pt ] \end{eqnarray}
\] となるので，発電機の効率\( \ \eta \ \)は，
\[
\begin{eqnarray}
\eta &=&\frac {P_{\mathrm {o}}}{P_{\mathrm {i}}}\times 100 \\[ 5pt ] &=&\frac {VI_{\mathrm {a}}}{EI_{\mathrm {a}}}\times 100 \\[ 5pt ] &=&\frac {V}{E}\times 100 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(3)
ワンポイント解説「2.直流機の誘導起電力\( \ E \ \)」の通り，回転軸が回らないよう固定すると，誘導起電力\( \ E \ \)が零となるため，電機子電圧と電機子抵抗での電圧降下が等しくなる。したがって，電機子に\( \ 3 \ \mathrm {V} \ \)の電圧を加えたときの電機子電流が\( \ 1 \ \mathrm {A} \ \)であるから，電機子抵抗\( \ R_{\mathrm {a}} \ \)の大きさは，
\[
\begin{eqnarray}
R_{\mathrm {a}} &=&\frac {3}{1} \\[ 5pt ] &=&3 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となる。
次に，電機子回路を開放した状態では，電機子電流\( \ I_{\mathrm {a}} \ \)が零であるから電機子抵抗での電圧降下はないので，回転子を定格回転数で駆動したときに電機子に発生する電圧はすべて誘導起電力\( \ E \ \)の大きさとなる。したがって，定格回転数での誘導起電力は\( \ E=15 \ \mathrm {V} \ \)となる。
以上から，定格運転時の等価回路は図2のようになる。

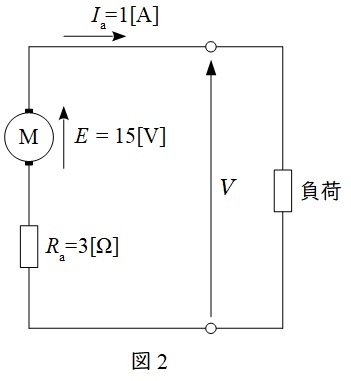
図2より，定格運転時の端子電圧\( \ V \ \)は，ワンポイント解説「1.直流他励発電機の電機子回路の等価回路」より，
\[
\begin{eqnarray}
V &=& E-R_{\mathrm {a}}I_{\mathrm {a}} \\[ 5pt ] &=& 15-3\times 1 \\[ 5pt ] &=&12 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となるので，定格運転時の効率\( \ \eta \ \)は，入力\( \ P_{\mathrm {i}} \ \)，出力\( \ P_{\mathrm {o}} \ \)とすると，ワンポイント解説「3.直流発電機の効率\( \ \eta \ \)」の通り，
\[
\begin{eqnarray}
\eta &=&\frac {P_{\mathrm {o}}}{P_{\mathrm {i}}}\times 100 \\[ 5pt ] &=&\frac {VI_{\mathrm {a}}}{EI_{\mathrm {a}}}\times 100 \\[ 5pt ] &=&\frac {V}{E}\times 100 \\[ 5pt ] &=&\frac {12}{15}\times 100 \\[ 5pt ] &=&80 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。