Contents
【問題】
【難易度】★★★☆☆(普通)
ある火力発電所にて,定格出力\( \ 350 \ \mathrm {MW} \ \)の発電機が下表に示すような運転を行ったとき,次の(a)及び(b)の問に答えよ。ただし,所内率は\( \ 2 \ \mathrm {%} \ \)とする。
発電機の運転状態
\[
\begin{array}{|c|c|}
\hline
時刻 & 発電機出力 \ \mathrm {[MW]} \\
\hline
0 \ 時 \ ~ \ 7 \ 時 & 130 \\
\hline
7 \ 時 \ ~ \ 12 \ 時 & 350 \\
\hline
12 \ 時 \ ~ \ 13 \ 時 & 200 \\
\hline
13 \ 時 \ ~ \ 20 \ 時 & 350 \\
\hline
20 \ 時 \ ~ \ 24 \ 時 & 130 \\
\hline
\end{array}
\]
(a) \( \ 0 \ \)時から\( \ 24 \ \)時の間の送電端電力量の値\( \ \mathrm {[MW\cdot h]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 4 \ 660 \ \) (2) \( \ 5 \ 710 \ \) (3) \( \ 5 \ 830 \ \) (4) \( \ 5 \ 950 \ \) (5) \( \ 8 \ 230 \ \)
(b) \( \ 0 \ \)時から\( \ 24 \ \)時の間に発熱量\( \ 54.70 \ \mathrm {MJ/kg} \ \)の\( \ \mathrm {LNG} \ \)(液化天然ガス)を\( \ 770 \ \mathrm {t} \ \)消費したとすると,この間の発電端熱効率の値\( \ \mathrm {[%]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 44 \ \) (2) \( \ 46 \ \) (3) \( \ 48 \ \) (4) \( \ 50 \ \) (5) \( \ 52 \ \)
【ワンポイント解説】
汽力発電所の効率に関する問題です。
発電端効率や送電端効率といった火力発電所における重要な指標を扱う問題です。
確実に理解するようにしましょう。
1.汽力発電所の各効率
汽力発電所で用いられる効率は以下の通りです。計算簡略化の為,すべて小数表記での計算となっています。効率の低下は燃料の使用量(支出)に影響するため,電力会社では熱効率が非常に重要なファクターとなっています。
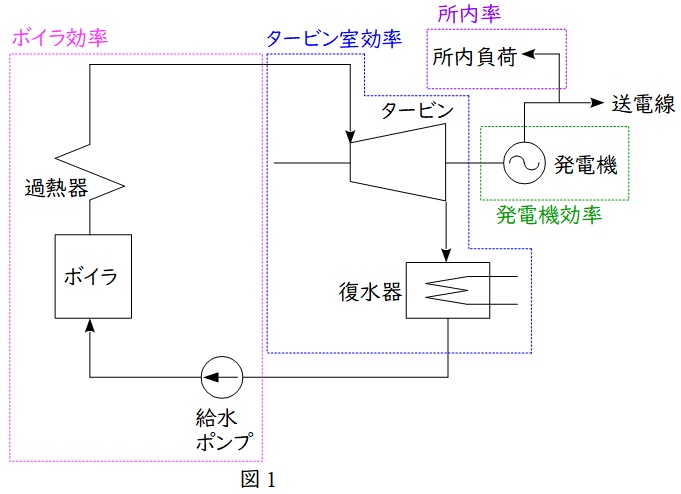
①ボイラ効率\( \ \eta _{\mathrm {B}} \ \)
ボイラで燃料を燃焼し,給水を蒸気にする際の熱交換率の指標です。排ガス損失等があります。
\[
\begin{eqnarray}
\eta _{\mathrm {B}}&=&\frac {ボイラの蒸気として得た熱量}{燃料使用量から換算した熱量} \\[ 5pt ]
\end{eqnarray}
\]
②タービン室効率\( \ \eta _{\mathrm {T}} \ \)
タービンに入った蒸気がどの程度のタービン出力になるかの効率で,タービン室という名前はタービンと復水器を合わせた効率という意味です。一般的な汽力発電所では一番ロスが大きい場所となります。
\[
\begin{eqnarray}
\eta _{\mathrm {T}}&=&\frac {タービン軸出力}{タービンへ入る蒸気の熱量} \\[ 5pt ]
\end{eqnarray}
\]
③発電機効率\( \ \eta _{\mathrm {G}} \ \)
発電機の風損や巻線抵抗損等を考慮した効率で,一般的な水素発電機では\( \ \mathrm {98~99%} \ \)程度となっています。
\[
\begin{eqnarray}
\eta _{\mathrm {G}}&=&\frac {発電機出力}{タービン軸出力} \\[ 5pt ]
\end{eqnarray}
\]
④発電端効率\( \ \eta _{\mathrm {P}} \ \)
発電ユニットの効率を表すもので,燃料の熱量がどの程度発電されたかを示す指標です。
\[
\begin{eqnarray}
\eta _{\mathrm {P}}&=&\frac {発電機出力}{燃料使用量から換算した熱量}&=&\eta _{\mathrm {B}}\cdot \eta _{\mathrm {T}}\cdot \eta _{\mathrm {G}} \\[ 5pt ]
\end{eqnarray}
\]
⑤送電端効率\( \ \eta _{\mathrm {S}} \ \)
発電端効率から所内率\( \ L \ \)を考慮し算出した効率で,発電所としての総合効率の指標となります。
\[
\begin{eqnarray}
\eta _{\mathrm {S}}&=&\eta _{\mathrm {P}}( 1-L ) \\[ 5pt ]
\end{eqnarray}
\]
2.\( \ \mathrm {[kJ]} \ \)と\( \ \mathrm {[kW\cdot h]} \ \)の変換
単位の定義より,
\[
\begin{eqnarray}
1 \ \mathrm {[kJ/s]} &=&1 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,両辺の単位に\( \ \mathrm {[s]} \ \)をかけると,
\[
\begin{eqnarray}
1 \ \mathrm {[kJ]} &=&1 \ \mathrm {[kW\cdot s]} \\[ 5pt ]
\end{eqnarray}
\]
となり,両辺に\( \ 1 \ \mathrm {[h]}=3600 \ \mathrm {[s]} \ \)を考慮して,\( \ 3600 \ \)をかけると,
\[
\begin{eqnarray}
3600 \ \mathrm {[kJ]} &=&1 \ \mathrm {[kW\cdot h]} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(a)解答:(2)
与えられている発電機の運転状態より,発電端電力量の合計\( \ W_{\mathrm {G}} \ \mathrm {[MW\cdot h]} \ \)は,
\[
\begin{eqnarray}
W_{\mathrm {G}} &=&130\times 7+350\times 5+200\times 1+350\times 7+130\times 4 \\[ 5pt ]
&=&5830 \ \mathrm {[MW\cdot h]} \\[ 5pt ]
\end{eqnarray}
\]
であり,所内率\( \ L=0.02 \ \)であるから,ワンポイント解説「1.汽力発電所の各効率」より,送電端電力量\( \ W_{\mathrm {S}} \ \mathrm {[MW\cdot h]} \ \)は,
\[
\begin{eqnarray}
W_{\mathrm {S}} &=&\left( 1-L\right) W_{\mathrm {G}} \\[ 5pt ]
&=&\left( 1-0.02\right) \times 5830 \\[ 5pt ]
&=&5713.4 → 5710 \ \mathrm {[MW\cdot h]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(b)解答:(4)
燃料消費量\( \ B=770 \ \mathrm {[t]} \ \),燃料発熱量\( \ H=54.70 \ \mathrm {[MJ/kg]} \ \)であるから,\( \ 0 \ \)時から\( \ 24 \ \)時の入熱\( \ Q_{\mathrm {i}} \ \mathrm {[MJ]} \ \)は,
\[
\begin{eqnarray}
Q_{\mathrm {i}} &=&BH \\[ 5pt ]
&=&770\times 10^{3}\times 54.70 \\[ 5pt ]
&≒&4.212\times 10^{7} \ \mathrm {[MJ]} \\[ 5pt ]
\end{eqnarray}
\]
となる。ワンポイント解説「2.\( \ \mathrm {[kJ]} \ \)と\( \ \mathrm {[kW\cdot h]} \ \)の変換」と用いれば,発電端効率\( \ \eta _{\mathrm {P}} \ \)は,
\[
\begin{eqnarray}
\eta _{\mathrm {P}} &=&\frac {発電機出力}{燃料使用量から換算した熱量} \\[ 5pt ]
&=&\frac {W_{\mathrm {G}}}{\displaystyle \frac {Q_{\mathrm {i}}}{3600}}\times 100 \\[ 5pt ]
&=&\frac {5830}{\displaystyle \frac {4.212\times 10^{7}}{3600}}\times 100 \\[ 5pt ]
&≒&49.8 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは