《電力》〈送電〉[R3:問16]電線の導体温度変化時の電線の実長及び水平張力に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

支持点の高さが同じで径間距離\( \ 150 \ \mathrm {m} \ \)の架空電線路がある。電線の質量による荷重が\( \ 20 \ \mathrm {N/m} \ \)，線膨張係数は\( \ 1 \ \mathrm {℃} \ \)につき\( \ 0.000 \ 018 \ \)である。電線の導体温度が\( \ -10 \ \mathrm {℃} \ \)のとき，たるみは\( \ 3.5 \ \mathrm {m} \ \)であった。次の(a)及び(b)の問に答えよ。ただし，張力による電線の伸縮はないものとし，その他の条件は無視するものとする。

(a)　電線の導体温度が\( \ 35 \ \mathrm {℃} \ \)のとき，電線の支持点間の実長の値\( \ \mathrm {[m]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 150.18 \ \)　　(2)　\( \ 150.23 \ \)　　(3)　\( \ 150.29 \ \)　
　(4)　\( \ 150.34 \ \)　　(5)　\( \ 151.43 \ \)

(b)　(a)と同じ条件のとき，電線の支持点間の最低点における水平張力の値\( \ \mathrm {[N]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 6 \ 272 \ \)　　(2)　\( \ 12 \ 863 \ \)　　(3)　\( \ 13 \ 927 \ \)　
　(4)　\( \ 15 \ 638 \ \)　　(5)　\( \ 17 \ 678 \ \)

【ワンポイント解説】

送電線のたるみや実長に関する問題です。
電線の長さと温度変化の関係は問題文で与えられることもありますが，本問のように与えられない場合もあります。
いずれも覚える公式となりますので，確実に暗記して試験を迎えるようにして下さい。

1.電線のたるみの公式
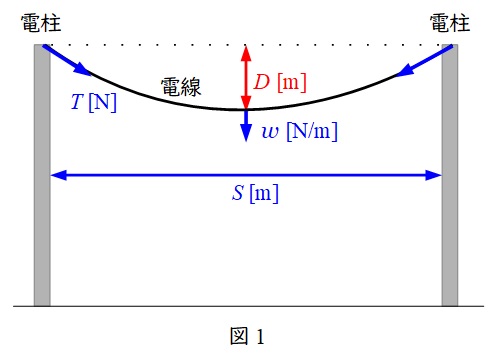
図1の通り，径間を\( \ S \ [ \mathrm {m} ] \ \)，水平張力\( \ T \ [ \mathrm {N} ] \ \)，電線\( \ 1 \ \mathrm {m} \ \)あたりの質量荷重\( \ w \ [ \mathrm {N/m} ] \ \)とすると，電線のたるみ\( \ D \ [\mathrm {m} ] \ \)は，
\[
\begin{eqnarray}
D&=&\frac {wS^{2}}{8T} \\[ 5pt ] \end{eqnarray}
\] となります。

2.電線の長さ\( \ L \ \)とたるみ\( \ D \ \)の関係
送電線の支持点間の距離\( \ S \ [ \mathrm {m} ] \ \)とたるみ\( \ D \ [ \mathrm {m} ] \ \)が与えられている時，電線の長さ\( \ L \ [ \mathrm {m} ] \ \)は，
\[
\begin{eqnarray}
L&=&S+\frac {8D^{2}}{3S} \\[ 5pt ] \end{eqnarray}
\] で求められます。

3.電線の長さと温度変化の関係
電線の温度が\( \ t_{1} \ \mathrm {[℃]} \ \)の時，長さが\( \ L_{1} \ \mathrm {[m]} \ \)であった場合，\( \ t_{2} \ \mathrm {[℃]} \ \)の時の長さ\( \ L_{2} \ \mathrm {[m]} \ \)は，線膨張係数を\( \ \alpha \ \)とすると，
\[
\begin{eqnarray}
L_{2}&=&L_{1}\left \{ 1+\alpha \left( t_{2}-t_{1}\right) \right\} \\[ 5pt ] \end{eqnarray}
\] となります。

【関連する「電気の神髄」記事】

　　電線のたるみ（弛度）・実長の式

【解答】

(a)解答：(4)
ワンポイント解説「2.電線の長さ\( \ L \ \)とたるみ\( \ D \ \)の関係」の通り，電線の導体温度が\( \ t_{1}=-10 \ \mathrm {℃} \ \)のときの実長\( \ L_{1} \ \mathrm {[m]} \ \)は，径間\( \ S=150 \ [ \mathrm {m} ] \ \)，電線のたるみ\( \ D_{1}=3.5 \ \mathrm {[m]} \ \)であるから，
\[
\begin{eqnarray}
L_{1}&=&S+\frac {8D_{1}^{2}}{3S} \\[ 5pt ] &=&150+\frac {8\times 3.5^{2}}{3\times 150} \\[ 5pt ] &≒&150.2178 \ \mathrm {[m]} \\[ 5pt ] \end{eqnarray}
\] となる。ワンポイント解説「3.電線の長さと温度変化の関係」の通り，電線の導体温度が\( \ t_{2}=35 \ \mathrm {℃} \ \)のときの実長\( \ L_{2} \ \mathrm {[m]} \ \)は，線膨張係数が\( \ \alpha =0.000 \ 018 \ \)であるから，
\[
\begin{eqnarray}
L_{2}&=&L_{1}\left \{ 1+\alpha \left( t_{2}-t_{1}\right) \right\} \\[ 5pt ] &=&150.2178\times \left[ 1+0.000 \ 018\times \left\{ 35-\left( -10 \right) \right\} \right] \\[ 5pt ] &≒&150.3395　→　150.34 \ \mathrm {[m]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(2)
ワンポイント解説「2.電線の長さ\( \ L \ \)とたるみ\( \ D \ \)の関係」より，電線の導体温度が\( \ t_{2}=35 \ \mathrm {℃} \ \)のときのたるみ\( \ D_{2} \ \mathrm {[m]} \ \)は，
\[
\begin{eqnarray}
L_{2}&=&S+\frac {8D_{2}^{2}}{3S} \\[ 5pt ] \frac {8D_{2}^{2}}{3S}&=&L_{2}-S \\[ 5pt ] D_{2}^{2}&=&\frac {3S\left( L_{2}-S\right) }{8} \\[ 5pt ] D_{2}&=&\sqrt {\frac {3S\left( L_{2}-S\right) }{8}} \\[ 5pt ] &=&\sqrt {\frac {3\times 150\times \left( 150.34-150\right) }{8}} \\[ 5pt ] &≒&4.373 \ \mathrm {[m]} \\[ 5pt ] \end{eqnarray}
\] であるから，ワンポイント解説「1.電線のたるみの公式」の通り，そのときの張力\( \ T \ \mathrm {[N]} \ \)は，電線の質量による荷重が\( \ w=20 \ \mathrm {[N/m]} \ \)であるから，
\[
\begin{eqnarray}
D_{2}&=&\frac {wS^{2}}{8T} \\[ 5pt ] T&=&\frac {wS^{2}}{8D_{2}} \\[ 5pt ] &=&\frac {20\times 150^{2}}{8\times 4.373} \\[ 5pt ] &≒&12 \ 863 \ \mathrm {[N]} \\[ 5pt ] \end{eqnarray}
\] と求められる。