《電力》〈送電〉[R4上:問8]送電線路での抵抗による全電力損失に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

受電端電圧が\( \ 20 \ \mathrm {kV} \ \)の三相\( \ 3 \ \)線式の送電線路において，受電端での電力が\( \ 2 \ 000 \ \mathrm {kW} \ \)，力率が\( \ 0.9 \ \)(遅れ)である場合，この送電線路での抵抗による全電力損失の値\( \ \mathrm {[kW]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし，送電線\( \ 1 \ \)線当たりの抵抗値は\( \ 9 \ \mathrm {\Omega } \ \)とし，線路のインダクタンスは無視するものとする。

　(1)　\( \ 12.3 \ \)　　(2)　\( \ 37.0 \ \)　　(3)　\( \ 64.2 \ \)　　(4)　\( \ 90.0 \ \)　　(5)　\( \ 111 \ \)

【ワンポイント解説】

送電線路の電力損失に関する問題です。
電流値を求め，電力損失を導出する頻出問題の一つですが，どうしても三相であることを忘れてしまう受験生が多いです。\( \ 3 \ \)倍するのをを忘れたときの誤答が必ずと言って良いほどありますので，電力損失を出すときには\( \ 3 \ \)倍することを忘れないようにして下さい。

1.三相線路の電力\( \ P \ \)と電圧\( \ V \ \)，電流\( \ I \ \)の関係
三相線路の電力\( \ P \ \mathrm {[W]} \ \)は，電圧\( \ V \ \mathrm {[V]} \ \)と電流\( \ I \ \mathrm {[A]} \ \)の位相差を\( \ \theta \ \)，力率を\( \ \cos \theta \ \)とすると，
\[
\begin{eqnarray}
P&=&\sqrt {3}VI\cos \theta \\[ 5pt ] \end{eqnarray}
\] となります。

2.三相線路の全電力損失
三相\( \ 3 \ \)線式の送電線路において送電線路の電力損失\( \ P_{\mathrm {L}} \ \mathrm {[W]} \ \)は，送電線路の抵抗\( \ r \ \mathrm {[\Omega ]} \ \)，送電線を流れる\( \ 1 \ \)線当たりの電流を\( \ I \ \mathrm {[A]} \ \)とすると，
\[
\begin{eqnarray}
P_{\mathrm {L}}&=&3rI^{2} \\[ 5pt ] \end{eqnarray}
\] で求められます。\( \ 3 \ \)線なので係数\( \ 3 \ \)を忘れないようにして下さい。

【解答】

解答：(5)
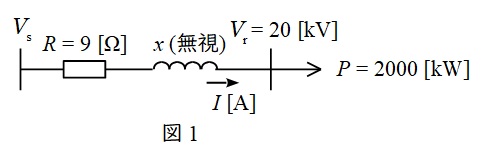
題意に沿って単線図を描くと図1のようになる。
受電端での電力\( \ P=2 \ 000 \ \mathrm {[kW]} \ \)，電圧\( \ V_{\mathrm {r}}=20 \ \mathrm {[kV]} \ \)，力率\( \ \cos \theta =0.9 \ \)であるから，送電線路に流れる電流\( \ I \ \mathrm {[A]} \ \)は，ワンポイント解説「1.三相線路の電力\( \ P \ \)と電圧\( \ V \ \)，電流\( \ I \ \)の関係」の通り，
\[
\begin{eqnarray}
P&=&\sqrt {3}VI\cos \theta \\[ 5pt ] I&=&\frac {P}{\sqrt {3}V\cos \theta } \\[ 5pt ] &=&\frac {2 \ 000\times 10^{3}}{\sqrt {3}\times 20\times 10^{3}\times 0.9} \\[ 5pt ] &=&64.15 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，送電線路での全電力損失\( \ P_{\mathrm {L}} \ \mathrm {[kW]} \ \)は，送電線\( \ 1 \ \)線当たりの抵抗\( \ r=9 \ \mathrm {[\Omega ]} \ \)であるから，ワンポイント解説「2.三相線路の全電力損失」より，
\[
\begin{eqnarray}
P_{\mathrm {L}}&=&3rI^{2} \\[ 5pt ] &=&3\times 9\times 64.15^{2} \\[ 5pt ] &≒&111 \ 111 \ \mathrm {[W]}　→　111 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。