Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
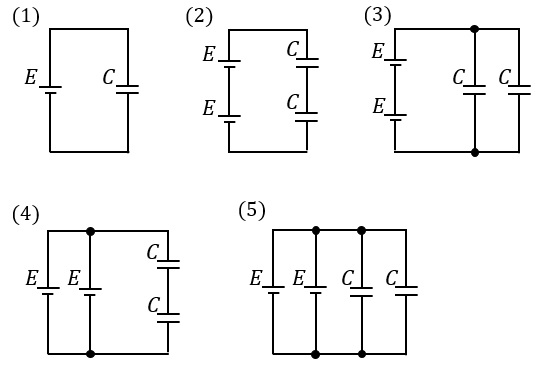
図に示す\( \ 5 \ \)種類の回路は,直流電圧\( \ E \ \mathrm {[V]} \ \)の電源と静電容量\( \ C \ \mathrm {[F]} \ \)のコンデンサの個数と組み合わせを異にしたものである。これらの回路のうちで,コンデンサ全体に蓄えられている電界のエネルギーが最も小さい回路を示す図として,正しいのは次のうちどれか。
【ワンポイント解説】
電源もしくはコンデンサが直並列された回路におけるコンデンサに蓄えられる静電エネルギーの比較に関する問題です。
静電エネルギーが静電容量に比例し電圧の\( \ 2 \ \)乗に比例することから,電源が直列→\( \ 4 \ \)倍,電源が並列→変化なし,コンデンサが並列→\( \ 2 \ \)倍,コンデンサが直列→\( \ \displaystyle \frac {1}{2} \ \)倍と判断できるようになると早く解けるようになりますので,チャレンジしてみて下さい。
1.コンデンサの合成静電容量
コンデンサ容量が\( \ C_{1} \ \mathrm {[F]} \ \)と\( \ C_{2} \ \mathrm {[F]} \ \)のコンデンサがある場合,直並列の合成静電容量\( \ C \ \mathrm {[F]} \ \)は下記の通りとなります。抵抗の場合と直並列が逆になることを知っておきましょう。
①並列回路の合成静電容量
\[
\begin{eqnarray}
C&=&C_{1}+C_{2} \\[ 5pt ]
\end{eqnarray}
\]
②直列回路の合成静電容量
\[
\begin{eqnarray}
\frac {1}{C}&=&\frac {1}{C_{1}}+\frac {1}{C_{2}} \\[ 5pt ]
\end{eqnarray}
\]
整理すると,
\[
\begin{eqnarray}
C&=&\frac {C_{1}C_{2}}{C_{1}+C_{2}} \\[ 5pt ]
\end{eqnarray}
\]
2.コンデンサの静電エネルギー\( \ W \ \)
コンデンサの静電エネルギー\( \ W \ \mathrm {[J]} \ \)は,コンデンサの静電容量\( \ C \ \mathrm {[F]} \ \)及びコンデンサにかかる電圧\( \ V \ \mathrm {[V]} \ \)とすると,
\[
\begin{eqnarray}
W &=&\frac {1}{2}CV^{2} \\[ 5pt ]
\end{eqnarray}
\]
であり,\( \ Q=CV \ \)の関係から,
\[
\begin{eqnarray}
W&=&\frac {1}{2}QV \\[ 5pt ]
&=&\frac {Q^{2}}{2C} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
解答:(4)
(1)
コンデンサに蓄えられるエネルギー\( \ W_{1} \ \mathrm {[J]} \ \)は,ワンポイント解説「2.コンデンサの静電エネルギー\( \ W \ \)」の通り,
\[
\begin{eqnarray}
W_{1} &=&\frac {1}{2}CE^{2} \ \mathrm {[J]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)
コンデンサの合成静電容量は,ワンポイント解説「1.コンデンサの合成静電容量」の通り,\( \ \displaystyle \frac {C\cdot C}{C+C}=\frac {C}{2} \ \mathrm {[F]} \ \)であるから,コンデンサに蓄えられるエネルギー\( \ W_{2} \ \mathrm {[J]} \ \)は,ワンポイント解説「2.コンデンサの静電エネルギー\( \ W \ \)」の通り,
\[
\begin{eqnarray}
W_{2} &=&\frac {1}{2}\cdot \frac {C}{2} \cdot \left( 2E\right) ^{2} \\[ 5pt ]
&=&CE^{2} \ \mathrm {[J]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)
コンデンサの合成静電容量は,ワンポイント解説「1.コンデンサの合成静電容量」の通り,\( \ \displaystyle C+C=2C \ \mathrm {[F]} \ \)であるから,コンデンサに蓄えられるエネルギー\( \ W_{3} \ \mathrm {[J]} \ \)は,ワンポイント解説「2.コンデンサの静電エネルギー\( \ W \ \)」の通り,
\[
\begin{eqnarray}
W_{3} &=&\frac {1}{2}\cdot 2C \cdot \left( 2E\right) ^{2} \\[ 5pt ]
&=&4CE^{2} \ \mathrm {[J]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)
コンデンサの合成静電容量は,ワンポイント解説「1.コンデンサの合成静電容量」の通り,\( \ \displaystyle \frac {C\cdot C}{C+C}=\frac {C}{2} \ \mathrm {[F]} \ \)であり,コンデンサ全体に加わる電圧が\( \ E \ \mathrm {[V]} \ \)あるから,コンデンサに蓄えられるエネルギー\( \ W_{4} \ \mathrm {[J]} \ \)は,ワンポイント解説「2.コンデンサの静電エネルギー\( \ W \ \)」の通り,
\[
\begin{eqnarray}
W_{4} &=&\frac {1}{2}\cdot \frac {C}{2} \cdot E ^{2} \\[ 5pt ]
&=&\frac {1}{4}CE^{2} \ \mathrm {[J]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)
コンデンサの合成静電容量は,ワンポイント解説「1.コンデンサの合成静電容量」の通り,\( \ \displaystyle C+C=2C \ \mathrm {[F]} \ \)であり,それぞれのコンデンサに加わる電圧が\( \ E \ \mathrm {[V]} \ \)あるから,コンデンサに蓄えられるエネルギー\( \ W_{5} \ \mathrm {[J]} \ \)は,ワンポイント解説「2.コンデンサの静電エネルギー\( \ W \ \)」の通り,
\[
\begin{eqnarray}
W_{5} &=&\frac {1}{2}\cdot 2C \cdot E ^{2} \\[ 5pt ]
&=&CE^{2} \ \mathrm {[J]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
以上から,蓄えられるエネルギーが最も小さいのは(4)となる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは