《理論》〈電子理論〉[H29:問18]演算増幅器を用いた回路に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★★（難しい）

演算増幅器を用いた回路について，次の(a)及び(b)の問に答えよ。

(a)　図1の回路の電圧増幅度\( \ \displaystyle \frac {v_{\mathrm {o}}}{v_{\mathrm {i}}} \ \)を\( \ 3 \ \)とするためには，\( \ \alpha \ \)をいくらにする必要があるか。\( \ \alpha \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

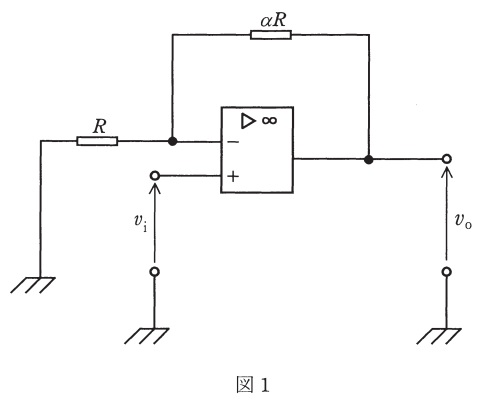
　(1)　\(0.3\)　　(2)　\(0.5\)　　(3)　\(1\)　　(4)　\(2\)　　(5)　\(3\)

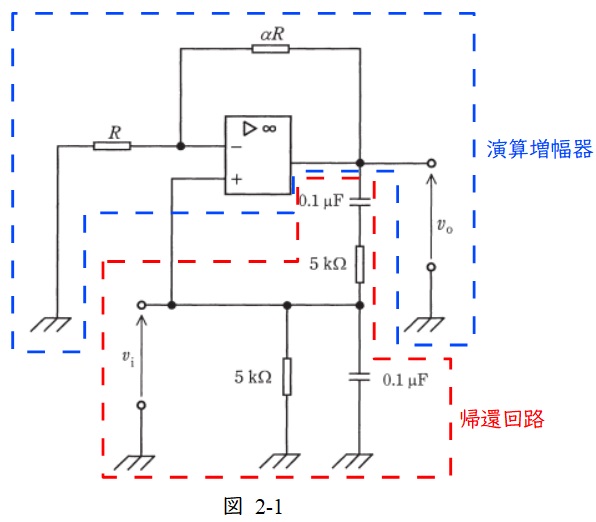
(b)　図2の回路は，図1の回路に，帰還回路として2個の\( \ 5 \ \mathrm {k\Omega } \ \)の抵抗と2個の\( \ 0.1 \ \mathrm {\mu F} \ \)のコンデンサを追加した発振回路である。発振の条件を用いて発振周波数の値\( \ \mathrm {f\left[ kHz\right] } \ \)を求め，最も近いものを次の(1)～(5)のうちから一つ選べ。

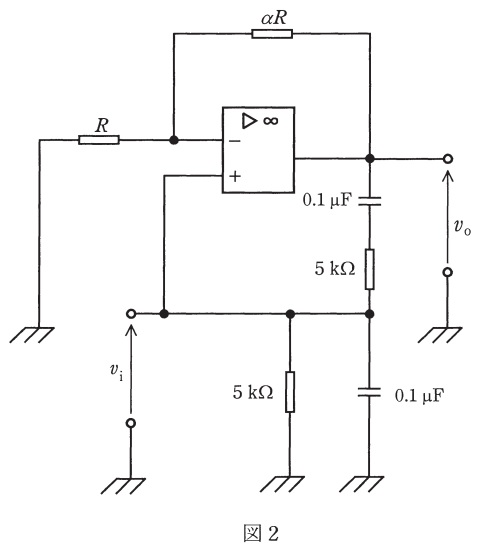
　(1)　\(0.2\)　　(2)　\(0.3\)　　(3)　\(0.5\)　　(4)　\(2\)　　(5)　\(3\)

【ワンポイント解説】

(a)はそれほど難しい問題ではありませんが，(b)の発振回路の発振条件の問題は，二種もしくは一種レベルの問題と思います。選択問題なので，本問ではなく問17を選択することも可能です。(a)の内容は三種でも頻出問題となりますので，よく理解しておきましょう。

1.理想的なオペアンプの特徴
　１．電圧増幅率が無限大である。したがって，無限大でない有限数が出力される時，入力端子間の電圧は\(0\mathrm {V}\)(バーチャルショート)となる。
　２．入力インピーダンスが無限大である。したがって入力端子に電流は流れない。
　３．出力インピーダンスがゼロである。

2.発振回路の発振条件
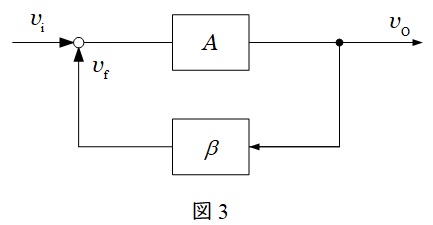
図3の回路において，演算増幅器\(A\)と帰還回路\(\beta \)とした時，
　　①\(A\beta ≧1\)
　　②\(A\beta \)の位相角が零
となるとき，発振回路は発振を継続します。オペアンプにおいては\(A=\infty \)なので，②のみ満たせばよいことになります。

【解答】

(a)解答：(4)
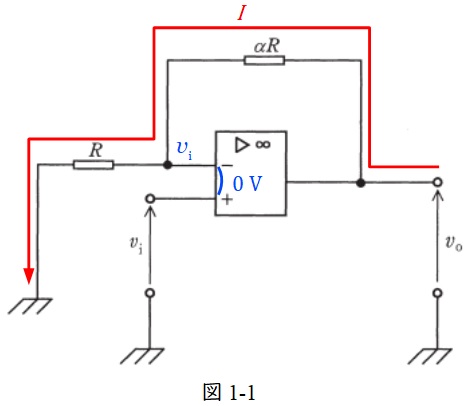
理想的なオペアンプの特性から，演算増幅器入口の電位は図1-1の通りとなる。
図1-1に示した通り，\( \ \alpha R \ \)に流れる電流\( \ I \ \)とすると，
\[
\begin{eqnarray}
I&=&\frac {v_{\mathrm {i}}}{R}　　　　　　・・・① \\[ 5pt ] \end{eqnarray}
\] となり，\( \ v_{\mathrm {o}} \ \)との関係は，
\[
\begin{eqnarray}
v_{\mathrm {o}}-v_{\mathrm {i}}&=&\alpha RI　　・・・② \\[ 5pt ] \end{eqnarray}
\] となるため，\( \ v_{\mathrm {o}}=3v_{\mathrm {i}} \ \)及び①を②に代入すると，
\[
\begin{eqnarray}
3v_{\mathrm {i}}-v_{\mathrm {i}} &=& \alpha R\frac {v_{\mathrm {i}}}{R} \\[ 5pt ] \alpha &=& 2 \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(2)
図2の演算増幅器と帰還回路を示すと，図2-1のようになる。
この時，帰還回路の帰還率\( \ \beta \ \)とすると，
\[
\begin{eqnarray}
\beta &=&\frac {v_{\mathrm {i}}}{v_{\mathrm {o}}} \\[ 5pt ] \end{eqnarray}
\] となる。さて，図2-1の回路において，\( \ R=5 \ \mathrm {k\Omega } \ \)と\( \ C=0.1 \ \mathrm {\mu F } \ \)の直列合成インピーダンス\( \ Z_{\mathrm {s}} \ \)及び並列合成インピーダンス\( \ Z_{\mathrm {p}} \ \)は，
\[
\begin{eqnarray}
Z_{\mathrm {s}}&=&R+\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ] Z_{\mathrm {p}}&=&\frac {R\cdot \frac {1}{\mathrm {j}2\pi f C}}{R+\frac {1}{\mathrm {j}2\pi f C}} \\[ 5pt ] &=&\frac {R}{1+\mathrm {j}2\pi f CR} \\[ 5pt ] \end{eqnarray}
\] と表すことができる。ここで，\( \ v_{\mathrm {i}} \ \)を\( \ Z_{\mathrm {s}} \ \)，\( \ Z_{\mathrm {p}} \ \)，\( \ v_{\mathrm {o}} \ \)で表すと，
\[
\begin{eqnarray}
v_{\mathrm {i}}&=&\frac {Z_{\mathrm {p}}}{Z_{\mathrm {s}}+Z_{\mathrm {p}}}v_{\mathrm {o}} \\[ 5pt ] \end{eqnarray}
\] となるから，\( \ \beta \ \)は，
\[
\begin{eqnarray}
\beta &=& \frac {v_{\mathrm {i}}}{v_{\mathrm {o}}}=\frac {Z_{\mathrm {p}}}{Z_{\mathrm {s}}+Z_{\mathrm {p}}} \\[ 5pt ] &=& \frac {\frac {R}{1+\mathrm {j}2\pi f CR}}{R+\frac {1}{\mathrm {j}2\pi f C}+\frac {R}{1+\mathrm {j}2\pi f CR}} \\[ 5pt ] &=& \frac {R}{\frac {\left( 1+\mathrm {j}2\pi f CR\right) ^{2}}{\mathrm {j}2\pi f C}+R} \\[ 5pt ] &=& \frac {R}{3R+\mathrm {j}\left( 2\pi f CR^{2}-\frac {1}{2\pi f C}\right)} \\[ 5pt ] &=& \frac {1}{3+\mathrm {j}\left( 2\pi f CR-\frac {1}{2\pi f CR}\right)} \\[ 5pt ] \end{eqnarray}
\] と求められる。ここで，発振回路の発振条件はワンポイント解説「2.発振回路の発振条件」より，\( \ A\beta \ \)の位相角が零の時である。ここで，\( \ A \ \)は実数であるから，\( \ \beta \ \)も実数とならなければならない。よって，\( \ \beta \ \)の虚数部が\( \ 0 \ \)となるため，
\[
\begin{eqnarray}
2\pi f CR-\frac {1}{2\pi f CR}&=&0 \\[ 5pt ] \end{eqnarray}
\] となる。これを\( \ f \ \)について解くと，
\[
\begin{eqnarray}
\left( 2\pi f CR\right) ^{2} &=& 1\\[ 5pt ] 2\pi f CR &=& 1\\[ 5pt ] f &=& \frac {1}{2\pi CR}
\end{eqnarray}
\] と求められる。各値を代入すると，
\[
\begin{eqnarray}
f &=& \frac {1}{2\times 3.14\times 0.1\times 10^{-6}\times 5\times 10^{3}} \\[ 5pt ] &≒& 0.3\times 10^{3} \ \mathrm {Hz} 　→　0.3 \ \mathrm {kHz}
\end{eqnarray}
\] となる。