《理論》〈電気回路〉[H21:問6]直並列した回路の電流値から抵抗値を求める計算問題

【問題】

【難易度】★☆☆☆☆（易しい）

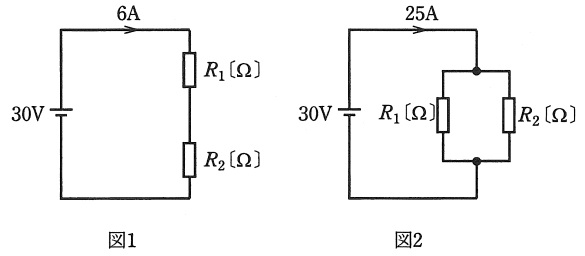
抵抗値が異なる抵抗\( \ R_{1} \ \mathrm {[\Omega ]} \ \)と\( \ R_{2} \ \mathrm {[\Omega ]} \ \)を図1のように直列に接続し，\( \ 30 \ \mathrm {[V]} \ \)の直流電圧を加えたところ，回路に流れる電流は\( \ 6 \ \mathrm {[A]} \ \)であった。次に，この抵抗\( \ R_{1} \ \mathrm {[\Omega ]} \ \)と\( \ R_{2} \ \mathrm {[\Omega ]} \ \)を図2のように並列に接続し，\( \ 30 \ \mathrm {[V]} \ \)の直流電圧を加えたところ，回路に流れる電流は\( \ 25 \ \mathrm {[A]} \ \)であった。このとき抵抗\( \ R_{1} \ \mathrm {[\Omega ]} \ \)，\( \ R_{2} \ \mathrm {[\Omega ]} \ \)のうち小さい方の抵抗 \( \ \mathrm {[\Omega ]} \ \)の値として，正しいのは次のうちどれか。

　(1)　\( \ 1 \ \)　　(2)　\( \ 1.2 \ \)　　(3)　\( \ 1.5 \ \)　　(4)　\( \ 2 \ \)　　(5)　\( \ 3 \ \)

【ワンポイント解説】

抵抗を直列にした場合と並列にした場合の電流値の違いから，抵抗値を求める問題です。
直並列の合成抵抗とオームの法則を理解していれば特に問題なく解ける問題かなと思います。

1.合成抵抗
抵抗\( \ R_{1} \ \)と\( \ R_{2} \ \)が与えられている時，それぞれの合成抵抗\( \ R \ \)は以下の式で与えられます。

①直列
直列合成抵抗\( \ R \ \)は，
\[
\begin{eqnarray}
R&=&R_{1}+R_{2} \\[ 5pt ] \end{eqnarray}
\] となります。

②並列
並列合成抵抗\( \ R \ \)は，
\[
\begin{eqnarray}
\frac {1}{R}&=&\frac {1}{R_{1}}+\frac {1}{R_{2}} \\[ 5pt ] \end{eqnarray}
\] となり，整理すると，
\[
\begin{eqnarray}
R&=&\frac {R_{1}R_{2}}{R_{1}+R_{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(4)
図1の回路における合成抵抗は\( \ R_{1}+R_{2} \ \)であるから，その大きさはオームの法則より，
\[
\begin{eqnarray}
R_{1}+R_{2}&=&\frac {30}{6} \\[ 5pt ] &=&5 \ \mathrm {[\Omega ]}　　・・・・・・・・・　① \\[ 5pt ] \end{eqnarray}
\] となる。また，図2の回路における合成抵抗は\( \ \displaystyle \frac {R_{1}R_{2}}{R_{1}+R_{2}} \ \)であるから，その大きさはオームの法則より，
\[
\begin{eqnarray}
\frac {R_{1}R_{2}}{R_{1}+R_{2}}&=&\frac {30}{25} \\[ 5pt ] \frac {R_{1}R_{2}}{5}&=&1.2 \\[ 5pt ] R_{1}R_{2}&=&6　　・・・・・・・・・・・　② \\[ 5pt ] \end{eqnarray}
\] となる。①式と②式を満たす\( \ R_{1} \ \mathrm {[\Omega ]} \ \)と\( \ R_{2} \ \mathrm {[\Omega ]} \ \)の組合せは\( \ 2 \ \mathrm {\Omega } \ \)と\( \ 3 \ \mathrm {\Omega } \ \)であるから，小さい方の抵抗の値は\( \ 2 \ \mathrm {\Omega } \ \)と求められる。