《理論》〈電磁気〉[H21:問17]平行平板電極内の電界分布と電圧に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

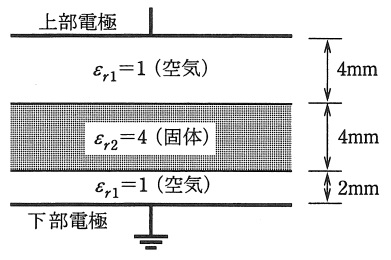
図に示すように，面積が十分に広い平行平板電極（電極間距離\( \ 10 \ \mathrm {[mm]} \ \)）が空気（比誘電率\( \ \varepsilon _{r1}=1 \ \)とする。）と，電極と同形同面積の厚さ\( \ 4 \ \mathrm {[mm]} \ \)で比誘電率\( \ \varepsilon _{r2}=4 \ \)の固体誘電体で構成されている。下部電極を接地し，上部電極に直流電圧\( \ V \ \mathrm {[kV]} \ \)を加えた。次の(a)及び(b)に答えよ。

ただし，固体誘電体の導電性及び電極と固体誘電体の端効果は無視できるものとする。

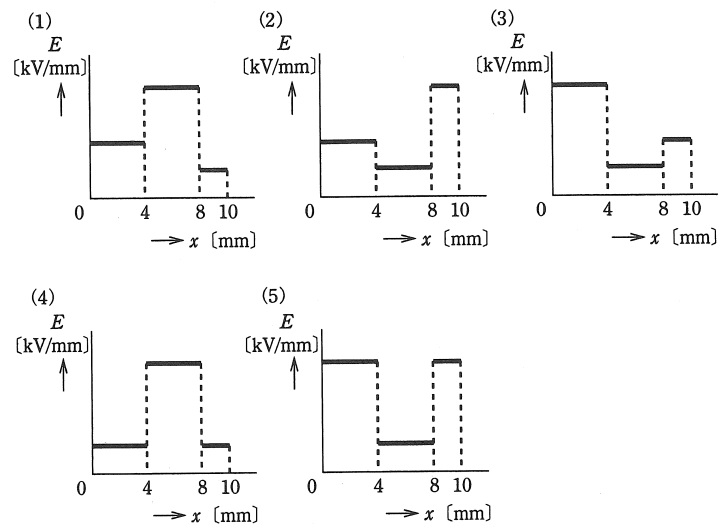
(a)　電極間の電界の強さ\( \ E \ \mathrm {[kV / mm]} \ \)のおおよその分布を示す図として，正しいのは次のうちどれか。

ただし，このときの電界の強さでは，放電は発生しないものとする。また，各図において，上部電極から下部電極に向かう距離を\( \ x \ \mathrm {[mm]} \ \)とする。

(b)　上部電極に加える電圧\( \ V \ \mathrm {[kV]} \ \)を徐々に増加し，下部電極側の空気中の電界の強さが\( \ 2 \ \mathrm {[kV / mm]} \ \)に達したときの電圧\( \ V \ \mathrm {[kV]} \ \)の値として，正しいのは次のうちどれか。

　(1)　\( \ 11 \ \)　　(2)　\( \ 14 \ \)　　(3)　\( \ 20 \ \)　　(4)　\( \ 44 \ \)　　(5)　\( \ 56 \ \)

【ワンポイント解説】

平行平板電極内の電界分布と電圧の導出に関する問題です。
\( \ \mathrm {B} \ \)問題としてはかなり解きやすい部類の問題となりますので，合格する上ではできれば両方とも得点したい問題です。必ずマスターするようにして下さい。

1.平行平板コンデンサの電界\( \ E \ \)と電圧\( \ V \ \)の関係
極板間の距離\( \ d \ \mathrm {[m]} \ \)の平行平板コンデンサに電圧\( \ V \ \mathrm {[V]} \ \)をかけると，極板間の電界\( \ E \ \mathrm {[V / m]} \ \)は，
\[
\begin{eqnarray}
E&=&\frac {V}{d} \\[ 5pt ] \end{eqnarray}
\] となります。

2.平行平板コンデンサの電束密度\( \ D \ \)と電界\( \ E \ \)の関係
極板間の誘電率を\( \ \varepsilon \ \mathrm {[F / m]} \ \)とすると，電束密度\( \ D \ \mathrm {[C / m^{2}]} \ \)と電界\( \ E \ \mathrm {[V / m]} \ \)には，
\[
\begin{eqnarray}
D&=&\varepsilon E \\[ 5pt ] \end{eqnarray}
\] の関係があります。

【解答】

(a)解答：(5)
\( \ 0≦x＜4 \ \)の空気中の電界を\( \ E_{1} \ \mathrm {[kV / mm]} \ \)，\( \ 4≦x≦8 \ \)の誘電体中の電界を\( \ E_{2} \ \mathrm {[kV / mm]} \ \)，\( \ 8＜x≦10 \ \)の空気中の電界を\( \ E_{3} \ \mathrm {[kV / mm]} \ \)とする。
平行平板電極内の電束密度は一定なので\( \ D \ \)とすれば，ワンポイント解説「2.平行平板コンデンサの電束密度\( \ D \ \)と電界\( \ E \ \)の関係」の通り，
\[
\begin{eqnarray}
E_{1}&=&\frac {D}{\varepsilon _{r1}} \\[ 5pt ] &=&\frac {D}{1} \\[ 5pt ] &=&D \\[ 5pt ] E_{2}&=&\frac {D}{\varepsilon _{r2}} \\[ 5pt ] &=&\frac {D}{4} \\[ 5pt ] E_{3}&=&\frac {D}{\varepsilon _{r3}} \\[ 5pt ] &=&\frac {D}{1} \\[ 5pt ] &=&D \\[ 5pt ] \end{eqnarray}
\] となるので，電界の強さの分布を示す図として適当なのは(5)と求められる。

(b)解答：(2)
題意より，\( \ E_{3}=2 \ \mathrm {[kV / mm]} \ \)であるから，(a)より，
\[
\begin{eqnarray}
E_{1}&=&E_{3} \\[ 5pt ] &=&2 \ \mathrm {[kV / mm]} \\[ 5pt ] E_{2}&=&\frac {E_{3}}{4} \\[ 5pt ] &=&\frac {2}{4} \\[ 5pt ] &=&0.5 \ \mathrm {[kV / mm]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，このときの電極間の電圧\( \ V \ \mathrm {[kV]} \ \)は，上部電極から空気の幅\( \ x_{1}=4 \ \mathrm {[mm]} \ \)，誘電体の幅\( \ x_{2}=4 \ \mathrm {[mm]} \ \)，空気の幅\( \ x_{3}=4 \ \mathrm {[mm]} \ \)とすると，ワンポイント解説「1.平行平板コンデンサの電界\( \ E \ \)と電圧\( \ V \ \)の関係」の通り，
\[
\begin{eqnarray}
V&=&E_{1}x_{1}+E_{2}x_{2}+E_{3}x_{3} \\[ 5pt ] &=&2\times 4+0.5\times 4+2\times 2 \\[ 5pt ] &=&14 \ \mathrm {[kV]} \\[ 5pt ] \end{eqnarray}
\] と求められる。