《理論》〈電気回路〉[H29:問7]直流回路の消費電力量に関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

図の回路において，電流の値\( \ I \ \left[ \mathrm {A}\right] \ \)は\( \ 4 \ \mathrm {A} \ \)よりも\( \ \fbox {　（ア）　} \ \)。このとき，抵抗\( \ R_{1} \ \)の中で動く電子の流れる向きは図の\( \ \fbox {　（イ）　} \ \)であり，電界の向きを併せて考えると，電気エネルギーは失われることになる。また，\( \ 0.25 \ \mathrm {s} \ \)の間に電源が供給する電力量に対し，同じ時間に抵抗\( \ R_{1} \ \)が消費する電力量の比は\( \ \fbox {　（ウ）　} \ \)である。抵抗は，消費した電力量だけの熱を発生することで温度が上昇するが，一方で，周囲との温度差に\( \ \fbox {　（エ）　} \ \)する熱を放出する。

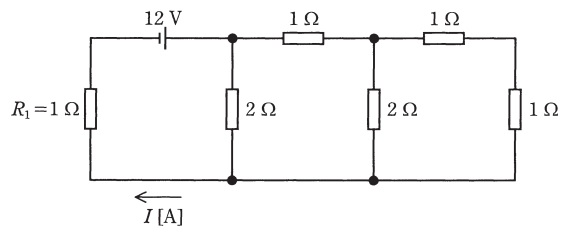
上記の記述中の空白箇所(ア)，(イ)，(ウ)及び(エ)に当てはまる組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。
\[
\begin{array}{ccccc}
& （ア） & （イ） & （ウ） & （エ） \\
\hline
(1) & 大きい & 上から下 & 0.5 & ほぼ比例 \\
\hline
(2) & 小さい & 上から下 & 0.25 & ほぼ反比例 \\
\hline
(3) & 大きい & 上から下 & 0.25 & ほぼ比例 \\
\hline
(4) & 小さい & 下から上 & 0.25 & ほぼ反比例 \\
\hline
(5) & 大きい & 下から上 & 0.5 & ほぼ反比例 \\
\hline
\end{array}
\]

【ワンポイント解説】

並列回路と直列回路の合成抵抗を求めてから，電力量と熱量の内容を問う複合的な問題となっています。計算はそれほど複雑ではないため，各公式を確認してしっかりと解きたい問題です。放出熱量は温度差が大きいほど大きくなりますが，寒い場所の方がお茶が冷めやすい等感覚的にわかると理想です。

1.直列回路と並列回路の合成抵抗
\( \ R_{1} \ \)と\( \ R_{2} \ \)の抵抗の合成抵抗\( \ R \ \)は以下の公式で求められます。
①直列回路の場合
\[
\begin{eqnarray}
R&=&R_{1}+R_{2} \\[ 5pt ] \end{eqnarray}
\]

②並列回路の場合
\[
\begin{eqnarray}
\frac {1}{R}&=&\frac {1}{R_{1}}+\frac {1}{R_{2}} \\[ 5pt ] \end{eqnarray}
\] すなわち，
\[
\begin{eqnarray}
R&=&\frac{R_{1}R_{2}}{R_{1}+R_{2}} \\[ 5pt ] \end{eqnarray}
\]

2.電源が供給する電力量\( \ W_{\mathrm {S}} \ \)と抵抗が消費する電力量\( \ W_{\mathrm {R}} \ \)
電源の電圧を\( \ V \ \)，抵抗\( \ R \ \)に流れる電流を\( \ I \ \)とすると，時間\( \ t \ \)の間に電源が供給する電力量\( \ W_{\mathrm {S}} \ \)と抵抗が消費する電力量\( \ W_{\mathrm {R}} \ \)は以下の通り求められます。
①電源が供給する電力量\( \ W_{\mathrm {S}} \ \)
\[
\begin{eqnarray}
W_{\mathrm {S}}&=&VIt \ \left[ \mathrm {W\cdot s}\right] \\[ 5pt ] \end{eqnarray}
\]

②抵抗が消費する電力量\( \ W_{\mathrm {R}} \ \)
\[
\begin{eqnarray}
W_{R}&=&RI^{2}t \ \left[ \mathrm {W\cdot s}\right] \\[ 5pt ] \end{eqnarray}
\]

【解答】

解答：(1)
(ア)
ワンポイント解説「1.直列と並列の合成抵抗」より，図1回路の合成抵抗は，下記の通り求めることができる。よって，回路は図1の下図のように書き換えることができる。
紫色の破線で囲まれた部分の合成抵抗：\(1+1=2 \ \left[ \Omega\right]\)
青色の破線で囲まれた部分の合成抵抗：\(\displaystyle \frac {2\times 2}{2+2}=1 \ \left[ \Omega\right]\)
緑色の破線で囲まれた部分の合成抵抗：\(1+1=2 \ \left[ \Omega\right]\)
赤色の破線で囲まれた部分の合成抵抗：\(\displaystyle \frac {2\times 2}{2+2}=1 \ \left[ \Omega\right]\)

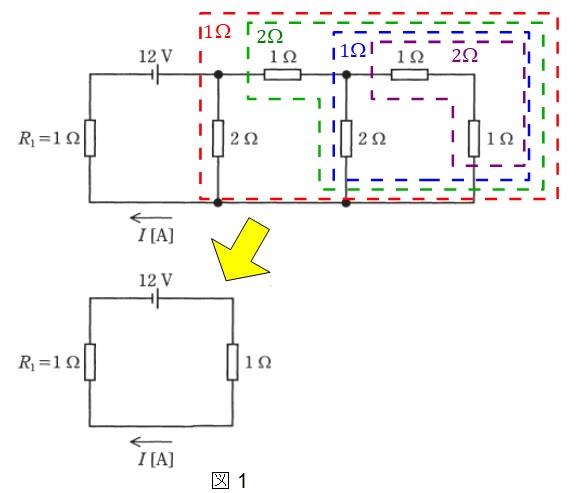
図1の回路を流れる電流\( \ I \ \)は，
\[
\begin{eqnarray}
I&=&\frac {12}{1+1} \\[ 5pt ] &=&6 \ \left[ \mathrm {A}\right] \\[ 5pt ] \end{eqnarray}
\] となり，\( \ 4 \ \mathrm {A} \ \)よりも大きくなる。

(イ)
電子の流れる向きはマイナスからプラス方向なので，図の上から下となる。

(ウ)
ワンポイント解説「2.電源が供給する電力量\( \ W_{\mathrm {S}} \ \)と抵抗が消費する電力量\( \ W_{\mathrm {R}} \ \)」より，\( \ 0.25 \ \mathrm {s} \ \)の間に電源が供給する電力量\( \ W_{\mathrm {S}} \ \)は，
\[
\begin{eqnarray}
W_{\mathrm {S}}&=&VIt \\[ 5pt ] &=&12\times 6\times 0.25 \\[ 5pt ] &=&18 \ \left[ \mathrm {W\cdot s}\right] \\[ 5pt ] \end{eqnarray}
\] となり，抵抗が消費する電力量\( \ W_{\mathrm {R}} \ \)は，
\[
\begin{eqnarray}
W_{\mathrm {R}}&=&RI^{2}t \\[ 5pt ] &=&1\times 6^{2}\times 0.25 \\[ 5pt ] &=&9 \ \left[ \mathrm {W\cdot s}\right] \\[ 5pt ] \end{eqnarray}
\] となる。よって，\( \ W_{\mathrm {S}} \ \)と\( \ W_{\mathrm {R}} \ \)の比は，
\[
\begin{eqnarray}
\frac {W_{\mathrm {R}}}{W_{\mathrm {S}}}&=&\frac {9}{18} \\[ 5pt ] &=&0.5 \\[ 5pt ] \end{eqnarray}
\] となる。

(エ)
抵抗は周囲の温度差に比例する熱を放出します。感覚的に周囲温度との差が大きければ大きいほど放熱量も多くなることは分かると思います。