《理論》〈電磁気〉[R01:問1]点電荷がつくる電位差の導出に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

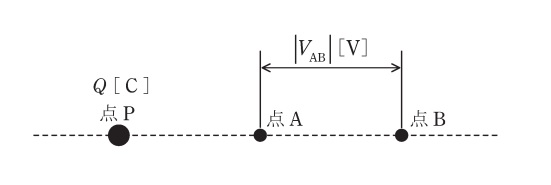
図のように，真空中に点\( \ \mathrm {P} \ \)，点\( \ \mathrm {A} \ \)，点\( \ \mathrm {B} \ \)が直線上に配置されている。点\( \ \mathrm {P} \ \)は\( \ Q \ \mathrm {[C]} \ \)の点電荷を置いた点とし，\( \ \mathrm {A} － \mathrm {B} \ \)間に生じる電位差の絶対値を\( \ \left| V_{\mathrm {AB}}\right| \ \mathrm {[V]} \ \)とする。次の(a)～(d)の四つの実験を個別に行ったとき，\( \ \left| V_{\mathrm {AB}}\right| \ \mathrm {[V]} \ \)の値が最小となるものと最大となるものの実験の組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。

［実験内容］
(a)　\( \ \mathrm {P} － \mathrm {A} \ \)間の距離を\( \ 2 \ \mathrm {m} \ \)，\( \ \mathrm {A} － \mathrm {B} \ \)間の距離を\( \ 1 \ \mathrm {m} \ \)とした。
(b)　\( \ \mathrm {P} － \mathrm {A} \ \)間の距離を\( \ 1 \ \mathrm {m} \ \)，\( \ \mathrm {A} － \mathrm {B} \ \)間の距離を\( \ 2 \ \mathrm {m} \ \)とした。
(c)　\( \ \mathrm {P} － \mathrm {A} \ \)間の距離を\( \ 0.5 \ \mathrm {m} \ \)，\( \ \mathrm {A} － \mathrm {B} \ \)間の距離を\( \ 1 \ \mathrm {m} \ \)とした。
(d)　\( \ \mathrm {P} － \mathrm {A} \ \)間の距離を\( \ 1 \ \mathrm {m} \ \)，\( \ \mathrm {A} － \mathrm {B} \ \)間の距離を\( \ 0.5 \ \mathrm {m} \ \)とした。

　(1)　(a)と(b)　　(2)　(a)と(c)　　(3)　(a)と(d)　　(4)　(b)と(c)　　(5)　(c)と(d)　　

【ワンポイント解説】

電位の公式を理解していれば解ける問題です。計算量が若干多めなのでできるだけ早く解けるよう学習するようにして下さい。

1.点電荷周辺の電位
真空中に電荷\( \ Q \ \)を置いた時，距離\( \ r \ \)離れた位置の電位\( \ V \ \)は，真空の誘電率を\( \ \varepsilon _{0} \ \)とすると，
\[
\begin{eqnarray}
V &=&\frac {Q}{4\pi \varepsilon _{0}r} \\[ 5pt ] \end{eqnarray}
\] となります。クーロンの法則\( \ \displaystyle F=\frac {Q_{1}Q_{2}}{4\pi \varepsilon _{0}r^{2}} \ \)や電界の式\( \ \displaystyle E=\frac {Q}{4\pi \varepsilon _{0}r^{2}} \ \)と似ているので合わせて覚えておきましょう。

【解答】

解答：(2)
(a)\( \ \mathrm {P} － \mathrm {A} \ \)間の距離を\( \ 2 \ \mathrm {m} \ \)，\( \ \mathrm {A} － \mathrm {B} \ \)間の距離を\( \ 1 \ \mathrm {m} \ \)
点\( \ \mathrm {A} \ \)の電位\( \ V_{\mathrm {A}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {A}} &=&\frac {Q}{4\pi \varepsilon _{0}\times 2} \\[ 5pt ] &=&\frac {Q}{8\pi \varepsilon _{0}} \\[ 5pt ] \end{eqnarray}
\] であり，点\( \ \mathrm {B} \ \)の電位\( \ V_{\mathrm {B}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {B}} &=&\frac {Q}{4\pi \varepsilon _{0}\times 3} \\[ 5pt ] &=&\frac {Q}{12\pi \varepsilon _{0}} \\[ 5pt ] \end{eqnarray}
\] となるので，電位差\( \ V_{\mathrm {AB}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {AB}} &=&V_{\mathrm {A}}-V_{\mathrm {B}} \\[ 5pt ] &=&\frac {Q}{8\pi \varepsilon _{0}}-\frac {Q}{12\pi \varepsilon _{0}} \\[ 5pt ] &=&\frac {Q}{24\pi \varepsilon _{0}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)\( \ \mathrm {P} － \mathrm {A} \ \)間の距離を\( \ 1 \ \mathrm {m} \ \)，\( \ \mathrm {A} － \mathrm {B} \ \)間の距離を\( \ 2 \ \mathrm {m} \ \)
点\( \ \mathrm {A} \ \)の電位\( \ V_{\mathrm {A}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {A}} &=&\frac {Q}{4\pi \varepsilon _{0}\times 1} \\[ 5pt ] &=&\frac {Q}{4\pi \varepsilon _{0}} \\[ 5pt ] \end{eqnarray}
\] であり，点\( \ \mathrm {B} \ \)の電位\( \ V_{\mathrm {B}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {B}} &=&\frac {Q}{4\pi \varepsilon _{0}\times 3} \\[ 5pt ] &=&\frac {Q}{12\pi \varepsilon _{0}} \\[ 5pt ] \end{eqnarray}
\] となるので，電位差\( \ V_{\mathrm {AB}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {AB}} &=&V_{\mathrm {A}}-V_{\mathrm {B}} \\[ 5pt ] &=&\frac {Q}{4\pi \varepsilon _{0}}-\frac {Q}{12\pi \varepsilon _{0}} \\[ 5pt ] &=&\frac {Q}{6\pi \varepsilon _{0}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(c)\( \ \mathrm {P} － \mathrm {A} \ \)間の距離を\( \ 0.5 \ \mathrm {m} \ \)，\( \ \mathrm {A} － \mathrm {B} \ \)間の距離を\( \ 1 \ \mathrm {m} \ \)
点\( \ \mathrm {A} \ \)の電位\( \ V_{\mathrm {A}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {A}} &=&\frac {Q}{4\pi \varepsilon _{0}\times 0.5} \\[ 5pt ] &=&\frac {Q}{2\pi \varepsilon _{0}} \\[ 5pt ] \end{eqnarray}
\] であり，点\( \ \mathrm {B} \ \)の電位\( \ V_{\mathrm {B}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {B}} &=&\frac {Q}{4\pi \varepsilon _{0}\times 1.5} \\[ 5pt ] &=&\frac {Q}{6\pi \varepsilon _{0}} \\[ 5pt ] \end{eqnarray}
\] となるので，電位差\( \ V_{\mathrm {AB}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {AB}} &=&V_{\mathrm {A}}-V_{\mathrm {B}} \\[ 5pt ] &=&\frac {Q}{2\pi \varepsilon _{0}}-\frac {Q}{6\pi \varepsilon _{0}} \\[ 5pt ] &=&\frac {Q}{3\pi \varepsilon _{0}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(d)\( \ \mathrm {P} － \mathrm {A} \ \)間の距離を\( \ 1 \ \mathrm {m} \ \)，\( \ \mathrm {A} － \mathrm {B} \ \)間の距離を\( \ 0.5 \ \mathrm {m} \ \)
点\( \ \mathrm {A} \ \)の電位\( \ V_{\mathrm {A}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {A}} &=&\frac {Q}{4\pi \varepsilon _{0}\times 1} \\[ 5pt ] &=&\frac {Q}{4\pi \varepsilon _{0}} \\[ 5pt ] \end{eqnarray}
\] であり，点\( \ \mathrm {B} \ \)の電位\( \ V_{\mathrm {B}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {B}} &=&\frac {Q}{4\pi \varepsilon _{0}\times 1.5} \\[ 5pt ] &=&\frac {Q}{6\pi \varepsilon _{0}} \\[ 5pt ] \end{eqnarray}
\] となるので，電位差\( \ V_{\mathrm {AB}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {AB}} &=&V_{\mathrm {A}}-V_{\mathrm {B}} \\[ 5pt ] &=&\frac {Q}{4\pi \varepsilon _{0}}-\frac {Q}{6\pi \varepsilon _{0}} \\[ 5pt ] &=&\frac {Q}{12\pi \varepsilon _{0}} \\[ 5pt ] \end{eqnarray}
\] と求められる。よって，電位差が最小となるものと最大となるものの実験の組合せは，(a)と(c)となる。