《法規》〈電気施設管理〉[R05上:問10]最大需要電力を抑えるためのファンの停止台数に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

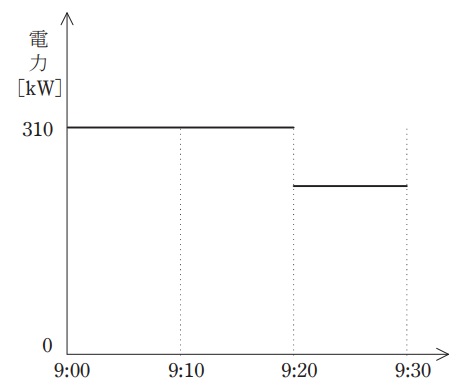
ある工場のある日の\( \ 9 \ \)時\( \ 00 \ \)分からの電力推移がグラフのとおりであった。この工場では日頃から最大需要電力（正時からの\( \ 30 \ \)分間ごとの平均使用電力のことをいう。以下同じ。）を\( \ 300 \ \mathrm {kW} \ \)未満に抑えるように負荷を管理しているが，その負荷の中で，換気用のファン（全て\( \ 5.5 \ \mathrm {kW} \ \)）は最大\( \ 8 \ \)台まで停止する運用を行っている。この日\( \ 9 \ \)時\( \ 00 \ \)分からファンは\( \ 10 \ \)台運転しているが，このままだと\( \ 9 \ \)時\( \ 00 \ \)分からの最大需要電力が\( \ 300 \ \mathrm {kW} \ \)以上になりそうなので，\( \ 9 \ \)時\( \ 20 \ \)分から\( \ 9 \ \)時\( \ 30 \ \)分の間，ファンを何台かと，その他の負荷を\( \ 10 \ \mathrm {kW} \ \)分だけ停止することにした。ファンは最低何台停止させる必要があるか，次の(1)～(5)のうちから一つ選べ。

なお，この工場の負荷は全て管理されており，負荷の増減は無いものとする。

　(1)　\( \ 0 \ \)　　(2)　\( \ 2 \ \)　　(3)　\( \ 4 \ \)　　(4)　\( \ 6 \ \)　　(5)　\( \ 8 \ \)

【ワンポイント解説】

需要電力を抑えるためのファンの停止台数を求める問題です。
契約電力というものがあり，それを踏まえて電力を管理する工場等もあると思います。本問は特別な公式を使用せずその場で読解し計算していく必要がある得意不得意が大きく分かれる問題です。

【解答】

解答：(3)
\( \ 9 \ \)時\( \ 20 \ \)分から\( \ 9 \ \)時\( \ 30 \ \)分の電力を\( \ P \ \mathrm {[kW]} \ \)とする。題意より，\( \ 9 \ \)時\( \ 00 \ \)分から\( \ 9 \ \)時\( \ 30 \ \)分までの需要電力を\( \ 300 \ \mathrm {kW} \ \)未満にしなければならないが，\( \ 9 \ \)時\( \ 00 \ \)分から\( \ 9 \ \)時\( \ 20 \ \)分までの出力が\( \ 310 \ \mathrm {kW} \ \)なので，
\[
\begin{eqnarray}
310\times 20+P\times 10 &=&300\times 30 \\[ 5pt ] 6 \ 200+10P &=&9 \ 000 \\[ 5pt ] 10P &=&2 \ 800 \\[ 5pt ] P &=&280 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] が，\( \ 9 \ \)時\( \ 20 \ \)分から\( \ 9 \ \)時\( \ 30 \ \)分の電力の上限となり，停止する電力は\( \ \Delta P=30 \ \mathrm {[kW]} \ \)必要であることがわかる。ファンの停止台数を\( \ X \ \)台とすると，ファンの消費電力が\( \ 5.5 \ \mathrm {kW} \ \)であり，その他の負荷を\( \ 10 \ \mathrm {kW} \ \)分停止していることから，
\[
\begin{eqnarray}
\Delta P &=&5.5X+10 \\[ 5pt ] 30 &=&5.5X+10 \\[ 5pt ] 5.5X &=&20 \\[ 5pt ] X &≒&3.64 \\[ 5pt ] \end{eqnarray}
\] となるので，ファンは\( \ 4 \ \)台以上停止しなければならない。