《機械》〈パワーエレクトロニクス〉[R05下:問16]降圧チョッパの原理と出力電流に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

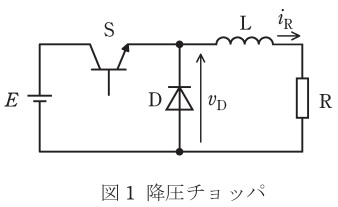
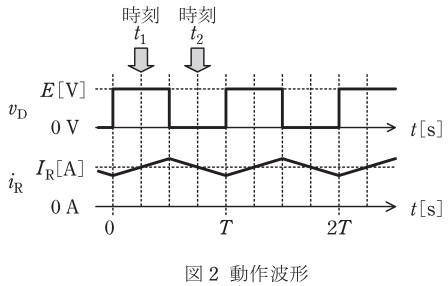
図1に示す降圧チョッパの回路は，電圧\( \ E \ \)の直流電源，スイッチングする半導体バルブデバイス\( \ \mathrm {S} \ \)，ダイオード\( \ \mathrm {D} \ \)，リアクトル\( \ \mathrm {L} \ \)，及び抵抗\( \ \mathrm {R} \ \)の負荷から構成されている。また，図2には，図1の回路に示すダイオード\( \ \mathrm {D} \ \)の電圧\( \ v_{\mathrm {D}} \ \)と負荷の電流\( \ i_{\mathrm {R}} \ \)の波形を示す。次の(a)及び(b)の問に答えよ。

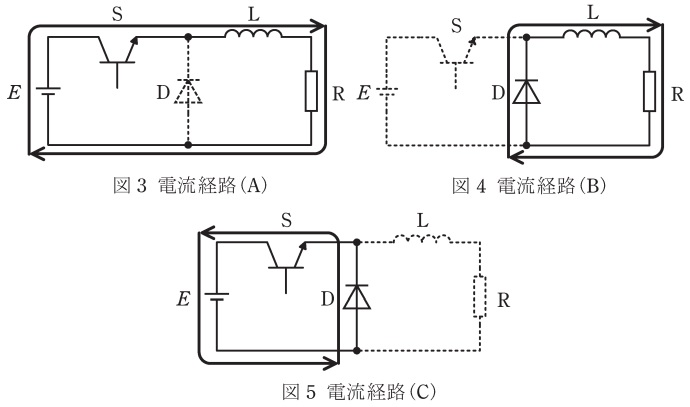
(a)　降圧チョッパの回路動作に関し，図3～図5に，実線で示した回路に流れる電流のループと方向を示した三つの電流経路を考える。図2の時刻\( \ t_{1} \ \)及び時刻\( \ t_{2} \ \)において，それぞれどの電流経路となるか。正しい組合せを次の(1)～(5)のうちから一つ選べ。
\[
\begin{array}{ccc}
& 時刻 \ t_{1} & 時刻 \ t_{2} \\
\hline
(1) & 　電流経路\left( \mathrm {A} \right)　 & 　電流経路\left( \mathrm {B} \right)　 \\
\hline
(2) & 　電流経路\left( \mathrm {A} \right)　 & 　電流経路\left( \mathrm {C} \right)　 \\
\hline
(3) & 　電流経路\left( \mathrm {B} \right)　 & 　電流経路\left( \mathrm {A} \right)　 \\
\hline
(4) & 　電流経路\left( \mathrm {B} \right)　 & 　電流経路\left( \mathrm {C} \right)　 \\
\hline
(5) & 　電流経路\left( \mathrm {C} \right)　 & 　電流経路\left( \mathrm {B} \right)　 \\
\hline
\end{array}
\]

(b)　電圧\( \ E \ \)が\( \ 100 \ \mathrm {V} \ \)，降圧チョッパの通流率が\( \ 50 \ ％ \ \)，負荷抵抗\( \ R \ \)が\( \ 2 \ \Omega \ \)とする。デバイス\( \ \mathrm {S} \ \)は周期\( \ T \ \)の高周波でスイッチングし，リアクトル\( \ \mathrm {L} \ \)の平滑作用により，図2に示す電流\( \ i_{\mathrm {R}} \ \)のリプル成分は十分小さいとする。電流\( \ i_{\mathrm {R}} \ \)の平均値\( \ I_{\mathrm {R}} \ \mathrm {[A]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 17.7 \ \)　　(2)　\( \ 25.0 \ \)　　(3)　\( \ 35.4 \ \)　　(4)　\( \ 50.1 \ \)　　(5)　\( \ 70.7 \ \)

【ワンポイント解説】

降圧チョッパに関する問題です。
パワーエレクトロニクスは動作原理を理解することが非常に重要となりますが，本問はその原理を理解するのにはとても良い問題となりますので，必ず理解しておくようにしましょう。
本問は平成30年問16からの再出題となります

1.降圧チョッパ
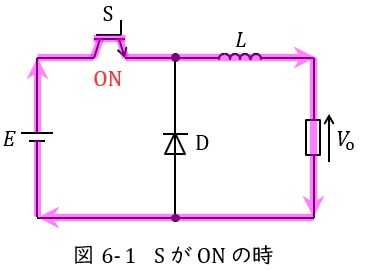
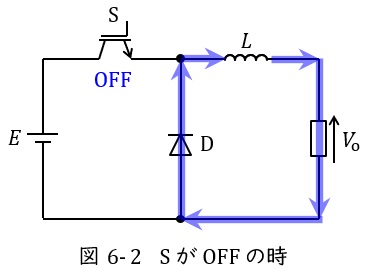
図6-1及び図6-2は降圧チョッパの例を示します。
スイッチ\( \ \mathrm {S} \ \)がオンになると，図6-1のように電源からの電流はスイッチ\( \ \mathrm {S} \ \)を通り，リアクトル\( \ L \ \)側に電流が流れますが，ダイオード\( \ \mathrm {D} \ \)は逆向きなので電流が流れません。
スイッチ\( \ \mathrm {S} \ \)がオフになると，図6-2のように電源から電流は流れず，リアクトル\( \ L \ \)に蓄えられているエネルギーから出力側と還流ダイオード\( \ \mathrm {D} \ \)に電流が流れます。
したがって降圧チョッパの出力電圧の平均値\( \ V_{\mathrm {o}} \ \)は，スイッチのオン時間を\( \ T_{\mathrm {on}} \ \)，オフ時間を\( \ T_{\mathrm {off}} \ \)とすると，
\[
\begin{eqnarray}
V_{\mathrm {o}}&=&\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}E \\[ 5pt ] \end{eqnarray}
\] で求められます。このとき，\( \ E \ \)の係数
\[
\begin{eqnarray}
\gamma &=&\frac {T_{\mathrm {ON}}}{T_{\mathrm {ON}}+T_{\mathrm {OFF}}} \\[ 5pt ] \end{eqnarray}
\] を通流率といいます。

【関連する「電気の神髄」記事】

　　降圧チョッパ回路の理論

【解答】

(a)解答：(1)
ワンポイント解説「1.降圧チョッパ」の通り，スイッチ\( \ \mathrm {S} \ \)が\( \ \mathrm {ON} \ \)の時，電流は電源\( \ E \ \)から流れ図3に示すような電流経路\( \ \mathrm {(A)} \ \)となり，スイッチ\( \ \mathrm {S} \ \)が\( \ \mathrm {OFF} \ \)の時，リアクトル\( \ \mathrm {L} \ \)に蓄えられたエネルギーが放出され，図4に示すような電流経路\( \ \mathrm {(B)} \ \)となります。時刻\( \ t_{1} \ \)では\( \ v_{\mathrm {D}}=E \ \mathrm {[V]} \ \)なのでスイッチ\( \ \mathrm {S} \ \)は\( \ \mathrm {ON} \ \)，時刻\( \ t_{2} \ \)では\( \ v_{\mathrm {D}}=0 \ \mathrm {[V]} \ \)なのでスイッチ\( \ \mathrm {S} \ \)は\( \ \mathrm {OFF} \ \)となります。

よって，時刻\( \ t_{1} \ \)では電流経路\( \ \mathrm {(A)} \ \)，時刻\( \ t_{2} \ \)では電流経路\( \ \mathrm {(B)} \ \)と求められます。

(b)解答：(2)
電源電圧\( \ E=100 \ \mathrm {[V]} \ \)，通流率\( \ \gamma =0.5 \ \)であるから，降圧チョッパの平均出力電圧\( \ V_{\mathrm {o}} \ \mathrm {[V]} \ \)は，ワンポイント解説「1.降圧チョッパ」の通り，
\[
\begin{eqnarray}
V_{\mathrm {o}} &=&\frac {T_{\mathrm {ON}}}{T_{\mathrm {ON}}+T_{\mathrm {OFF}}}E \\[ 5pt ] &=&\gamma E \\[ 5pt ] &=&0.5\times 100 \\[ 5pt ] &=&50 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，負荷抵抗\( \ R=2 \ \mathrm {[\Omega ]} \ \)であるので，電流\( \ i_{\mathrm {R}} \ \)の平均値\( \ I_{\mathrm {R}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {R}} &=&\frac {V_{\mathrm {o}}}{R} \\[ 5pt ] &=&\frac {50}{2} \\[ 5pt ] &=&25 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。