《電力》〈配電〉[R06上:問11]送配電方式として広く採用されている交流三相方式に関する論説問題

【問題】

【難易度】★★★☆☆（普通）

送配電方式として広く採用されている交流三相方式に関する記述として，誤っているものを次の(1)～(5)のうちから一つ選べ。

(1)　電源側を$\ \mathrm {Y} \ $結線としたうえで，中性線を施設して三相$\ 4 \ $線式とすると，線間電圧と相電圧の両方を容易に取り出して利用できるようになる。

(2)　同一材料の電線を使用して，同じ線間電圧で同じ電力を同じ距離に，同じ損失で送電する場合に必要な電線の総重量は，三相$\ 3 \ $線式でも単相$\ 2 \ $線式と同等である。

(3)　回転磁界が容易に得られるため，動力源として三相誘導電動機の活用に便利である。

(4)　三相回路が平衡している場合，三相交流全体の瞬時電力は時間に無関係な一定値となり，単相交流の場合のように脈動しないという利点がある。

(5)　発電機では，同じ出力ならば，単相の場合に比べるとより小形に設計できて効率がよい。

【ワンポイント解説】

交流三相方式の特徴に関する問題です。
単相方式との比較はもちろん計算で導出できるのが理想ですが，本問のような問題である場合，計算する時間はないので知識として知っておく必要があります。
本問は平成17年問7からの再出題となります。

1.各配電方式の送電電力，電力損失，電線重量の比較
単相$\ 2 \ $線式方式を基準（$\ 100 \ $）としたときの同条件下での各配電方式の送電電力，電力損失，電線重量は下表の通りとなります。もちろん導出できるのが理想ですが，ある程度概要を頭に入れておくと良いでしょう。

$$\begin{array}{|c|c|c|c|} \hline & 　送電電力　 & 　電力損失　 & 　電線重量　 \\ \hline 単相 \ 2 \ 線式 & 　100　 & 　100　 & 　100　 \\ \hline 単相 \ 3 \ 線式 & 　133　 & 　25　 & 　37.5　 \\ \hline 三相 \ 3 \ 線式 & 　115　 & 　50　 & 　75　 \\ \hline 三相 \ 4 \ 線式 & 　150　 & 　16.7　 & 　33.3　 \\ \hline \end{array}$$

【解答】

解答：(2)
(1)：正しい
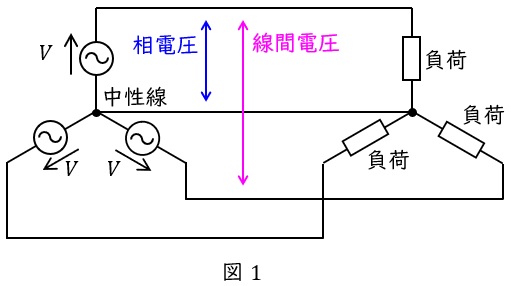
問題文の通り，電源側を$\ \mathrm {Y} \ $結線としたうえで，中性線を施設して三相$\ 4 \ $線式とすると，図1に示すように，線間電圧と相電圧の両方を容易に取り出して利用できるようになります。

(2)：誤り
ワンポイント解説「1.各配電方式の送電電力，電力損失，電線重量の比較」の通り，同一材料の電線を使用して，同じ線間電圧で同じ電力を同じ距離に，同じ損失で送電する場合に必要な電線の総重量は，三相$\ 3 \ $線式の方が小さくなります。
同じ線間電圧$\ V \ \mathrm {[V]} \ $，電力$\ P \ \mathrm {[W]} \ $，同じ距離$\ l \ \mathrm {[m]} \ $，同じ損失$\ P_{\mathrm {L}} \ \mathrm {[W]} \ $，同じ力率$\ \cos \theta \ $とした場合，単相$\ 2 \ $線式の線路電流$\ I_{2} \ \mathrm {[A]} \ $及び三相$\ 3 \ $線式の線路電流$\ I_{3} \ \mathrm {[A]} \ $は，

$$\begin{eqnarray} P&=&VI_{2}\cos \theta \\[ 5pt ] I_{2}&=&\frac {P}{V\cos \theta } \\[ 5pt ] P&=&\sqrt {3}VI_{3}\cos \theta \\[ 5pt ] I_{3}&=&\frac {P}{\sqrt {3}V\cos \theta }=\frac {I_{2}}{\sqrt {3}} \\[ 5pt ] \end{eqnarray}$$ となり，電力損失との関係より，それぞれの$\ 1 \ $線あたりの線路抵抗$\ r_{2} \ \mathrm {[\Omega ]} \ $及び$\ r_{3} \ \mathrm {[\Omega ]} \ $は，
$$\begin{eqnarray} P_{\mathrm {L}}&=&2r_{2}I_{2}^{2} \\[ 5pt ] r_{2}&=&\frac {P_{\mathrm {L}}}{2I_{2}^{2}} \\[ 5pt ] P_{\mathrm {L}}&=&3r_{3}I_{3}^{2} \\[ 5pt ] &=&r_{3}I_{2}^{2}　\left( ∵I_{3}=\frac {I_{2}}{\sqrt {3}}\right) \\[ 5pt ] r_{3}&=&\frac {P_{\mathrm {L}}}{I_{2}^{2}}=2r_{2} \\[ 5pt ] \end{eqnarray}$$ となります。$\ \displaystyle R=\rho \frac {l}{S} \ $の関係より，同材質で同じ長さである場合抵抗値は断面積に反比例するので，単相$\ 2 \ $線式の断面積$\ S_{2} \ \mathrm {[m^{2}]} \ $及び三相$\ 3 \ $線式の断面積$\ S_{3} \ \mathrm {[m^{2}]} \ $の関係は，
$$\begin{eqnarray} \frac {S_{2}}{S_{3}}&=&\frac {r_{3}}{r_{2}} \\[ 5pt ] &=&\frac {2r_{2}}{r_{2}} \\[ 5pt ] &=&2 \\[ 5pt ] \end{eqnarray}$$ となるので，それぞれの電線の総重量$\ W_{2} \ \mathrm {[kg]} \ $と$\ W_{3} \ \mathrm {[kg]} \ $の比は，
$$\begin{eqnarray} \frac {W_{2}}{W_{3}}&=&\frac {2S_{2}l}{3S_{3}l} \\[ 5pt ] &=&\frac {2\times 2S_{3}}{3S_{3}} \\[ 5pt ] &=&\frac {4}{3} \\[ 5pt ] \end{eqnarray}$$ となり，単相$\ 2 \ $線式の方が大きくなります。

(3)：正しい
問題文の通り，三相方式は回転磁界が容易に得られるため，動力源として三相誘導電動機の活用に便利となります。回転磁界の発生メカニズムは機械科目の範囲となりますので，しっかりと理解されたい方は令和5年上期機械科目問3等を学習すると良いでしょう。

(4)：正しい
問題文の通り，三相回路が平衡している場合，三相交流全体の瞬時電力は時間に無関係な一定値となり，単相交流の場合のように脈動しません。こちらでは割愛しますが，実際に計算してみるとわかるかと思います。

(5)：正しい
問題文の通り，三相の場合同じ出力，同電圧ならば，電流値は小さくなるため小形に設計できることになります。