《法規》〈電気施設管理〉[H19:問12]日負荷曲線からの変圧器の全日効率の導出に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

配電線路に接続された，定格容量\( \ 20 \ \mathrm {[kV\cdot A]} \ \)，定格二次電流\( \ 200 \ \mathrm {[A]} \ \)，定格電圧時の鉄損\( \ 150 \ \mathrm {[W]} \ \)，定格負荷時の鋼損\( \ 270 \ \mathrm {[W]} \ \)の単相変圧器がある。
この変圧器の二次側の日負荷曲線が図のような場合について，次の(a)及び(b)に答えよ。ただし，負荷の力率は\( \ 100 \ \mathrm {[％]} \ \)とする。

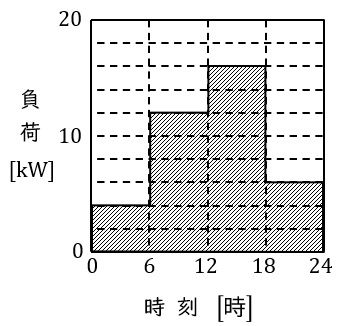
(a)　変圧器の\( \ 1 \ \)日の損失電力量\( \ \mathrm {[kW\cdot h]} \ \)の値として，最も近いのは次のうちどれか。

　(1)　\( \ 3.68 \ \)　　(2)　\( \ 3.91 \ \)　　(3)　\( \ 5.43 \ \)　　(4)　\( \ 7.00 \ \)　　(5)　\( \ 7.50 \ \)

(b)　変圧器の全日効率\( \ \mathrm {[％]} \ \)の値として，最も近いのは次のうちどれか。

　(1)　\( \ 96.8 \ \)　　(2)　\( \ 97.0 \ \)　　(3)　\( \ 97.7 \ \)　　(4)　\( \ 98.4 \ \)　　(5)　\( \ 99.0 \ \)

【ワンポイント解説】

負荷が接続された変圧器の効率に関する問題です。
鉄損が負荷によらず一定，銅損が負荷の\( \ 2 \ \)乗に比例することを覚えていれば，難解な計算を必要としないため問題なく解けるかと思います。
計算間違いに注意して完答を目指すようにして下さい。

1.変圧器の効率\( \ \eta \ \)
変圧器の損失は鉄損\( \ p_{\mathrm {i}} \ \mathrm {[W]} \ \)と銅損\( \ p_{\mathrm {c}} \ \mathrm {[W]} \ \)があり，\( \ p_{\mathrm {i}} \ \mathrm {[W]} \ \)は負荷によらず一定であり，\( \ p_{\mathrm {c}} \ \mathrm {[W]} \ \)は負荷（電流）の\( \ 2 \ \)乗に比例します。従って，定格出力\( \ P_{\mathrm {n}} \ \mathrm {[W]} \ \)で利用率\( \ \alpha \ \)の時の変圧器の効率\( \ \eta \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
\eta &=&\frac {出力}{入力}\times 100 \\[ 5pt ] &=&\frac {出力}{出力+損失}\times 100 \\[ 5pt ] &=&\frac {\alpha P_{\mathrm {n}}}{\alpha P_{\mathrm {n}}+p_{\mathrm {i}}+\alpha ^{2}p_{\mathrm {c}}}\times 100 \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(a)解答：(3)
\( \ 0 \sim 6 \ \)時の銅損を\( \ P_{c1} \ \mathrm {[W]} \ \)，\( \ 6 \sim 12 \ \)時の銅損を\( \ P_{c2} \ \mathrm {[W]} \ \)，\( \ 12 \sim 18 \ \)時の銅損を\( \ P_{c3} \ \mathrm {[W]} \ \)，\( \ 18 \sim 24 \ \)時の銅損を\( \ P_{c4} \ \mathrm {[W]} \ \)とすると，
\[
\begin{eqnarray}
P_{c1} &=&\left( \frac {4}{20} \right) ^{2}\times 270 \\[ 5pt ] &=&10.8 \ \mathrm {[W]} \\[ 5pt ] P_{c2} &=&\left( \frac {12}{20} \right) ^{2}\times 270 \\[ 5pt ] &=&97.2 \ \mathrm {[W]} \\[ 5pt ] P_{c3} &=&\left( \frac {16}{20} \right) ^{2}\times 270 \\[ 5pt ] &=&172.8 \ \mathrm {[W]} \\[ 5pt ] P_{c4} &=&\left( \frac {6}{20} \right) ^{2}\times 270 \\[ 5pt ] &=&24.3 \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] となり，鉄損\( \ P_{i}=150 \ \mathrm {[W]} \ \)は一定であるから，\( \ 1 \ \)日の損失電力量\( \ W_{l} \ \mathrm {[kW\cdot h]} \ \)は，
\[
\begin{eqnarray}
W_{l} &=&6P_{c1}+6P_{c2}+6P_{c3}+6P_{c4}+24P_{i} \\[ 5pt ] &=&6\left( P_{c1}+P_{c2}+P_{c3}+P_{c4}\right) +24P_{i} \\[ 5pt ] &=&6\times \left( 10.8+97.2+172.8+24.3\right) +24\times 150 \\[ 5pt ] &≒&5 \ 430 \ \mathrm {[W\cdot h]}　→　5.43 \ \mathrm {[kW\cdot h]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(3)
日負荷曲線より，一日の供給電力量\( \ W \ \mathrm {[kW\cdot h]} \ \)は，
\[
\begin{eqnarray}
W &=&6\times 4+6\times 12+6\times 16+6\times 6 \\[ 5pt ] &=&228 \ \mathrm {[kW\cdot h]} \\[ 5pt ] \end{eqnarray}
\] であるから，全日効率\( \ \eta \ \mathrm {[％]} \ \)は，ワンポイント解説「1.変圧器の効率\( \ \eta \ \)」の通り，
\[
\begin{eqnarray}
\eta &=&\frac {W}{W+W_{l}}\times 100 \\[ 5pt ] &=&\frac {228}{228+5.43}\times 100 \\[ 5pt ] &≒&97.7 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。