Contents
【問題】
【難易度】★★★☆☆(普通)
一次側の巻数が\(N_{1}\),二次側の巻数が\(N_{2}\)で製作された,同一仕様3台の単相変圧器がある。これらを用いて一次側を\(\Delta \)結線,二次側を\(\mathrm {Y}\)結線として抵抗負荷,一次側に三相発電機を接続した。発電機を電圧\(440 \ \mathrm {V}\),出力\(100 \ \mathrm {kW}\),力率\(1.0\)で運転したところ,二次電流は三相平衡の\(17.5 \ \mathrm {A}\)であった。この単相変圧器の巻数比\(\displaystyle \frac {N_{1}}{N_{2}}\)の値として,最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし,変圧器の励磁電流,インピーダンス及び損失は無視するものとする。
(1) \(0.13\) (2) \(0.23\) (3) \(0.40\) (4) \(4.3\) (5) \(7.5\)
【ワンポイント解説】
変圧器の巻数比による電流の変化を求めるのと,\(\mathrm {Y-\Delta }\)結線の特徴を理解していないと解けない問題です。ただし,どちらも非常に重要な内容なので,よく理解しておきましょう。
1.変圧器の一次側と二次側電圧と電流の関係
一次側と二次側の巻数比が\(N_{1}:N_{2}\)である時,
\[
\frac {N_{1}}{N_{2}}=\frac {V_{1}}{V_{2}}=\frac {I_{2}}{I_{1}}
\]
となります。
【解答】
解答:(2)
問題文の関係を図に示すと,図1のようになる。
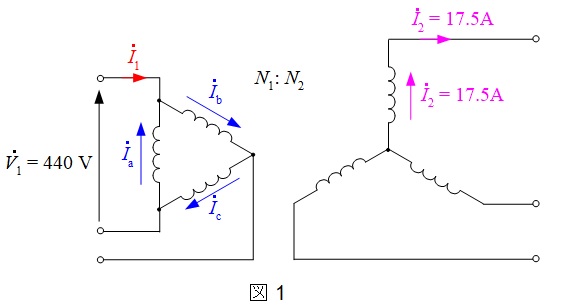
発電機の電圧\(V_{1}= 440 \ \mathrm {V}\)と出力\(P_{1}=100 \ \mathrm {kW}\)より,一次電流の大きさ\(I_{1}\)は,力率が1であるから,
\[
\begin{eqnarray}
I_{1}&=&\frac {P_{1}}{\sqrt{3}V_{1}} \\[ 5pt ]
&=&\frac {100\times 10^{3}}{\sqrt{3}\times 440} \\[ 5pt ]
&≒&131.2 \ \mathrm {[A]}
\end{eqnarray}
\]
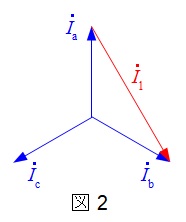
となる。ここで,図1に示すように\(\Delta \)巻線に流れる電流を\(\dot {I_{\mathrm {a}}}\),\(\dot {I_{\mathrm {b}}}\),\(\dot {I_{\mathrm {c}}}\)とすると,各電流のベクトル図は図2のように描ける。
図2より,\(\Delta \)巻線に流れる電流\(\dot {I_{\mathrm {a}}}\)の大きさ\(I_{\mathrm {a}}\)は\(I_{1}\)の\(\displaystyle \frac {1}{\sqrt {3}}\)倍であるので,
\[
\begin{eqnarray}
I_{\mathrm {a}}&=&\frac {1}{\sqrt {3}}I_{1} \\[ 5pt ]
&=&\frac {1}{\sqrt {3}}\times 131.2 \\[ 5pt ]
&≒&75.75 \ \mathrm {[A]}
\end{eqnarray}
\]
となる。
ワンポイント解説「1.変圧器の一次側と二次側電圧と電流の関係」より,巻数比\(\displaystyle \frac {N_{1}}{N_{2}}\)は,
\[
\begin{eqnarray}
\frac {N_{1}}{N_{2}}&=&\frac {I_{2}}{I_{\mathrm {a}}} \\[ 5pt ]
&=&\frac {17.5}{75.75} \\[ 5pt ]
&≒&0.23
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは