Contents
【問題】
【難易度】★★★★☆(やや難しい)
情報の一時的な記憶回路として用いられるフリップフロップ(\( \ \mathrm {FF} \ \))回路について,次の(a)及び(b)の問に答えよ。
(a) \( \ \mathrm {FF} \ \)回路に関する記述として,誤っているものを次の(1)~(5)のうちから一つ選べ。ただし,(1)~(4)における出力とは,反転しない\( \ \mathrm {Q} \ \)のことである。
(1) \( \ \mathrm {RS – FF} \ \)においては,クロックパルスの動作タイミングで入力\( \ R \ \)と\( \ S \ \)がそれぞれ\( \ 1 \ \)と\( \ 0 \ \)の場合に\( \ 0 \ \)を,入力\( \ R \ \)と\( \ S \ \)がそれぞれ\( \ 0 \ \)と\( \ 1 \ \)の場合に\( \ 1 \ \)を出力する。入力\( \ R \ \)と\( \ S \ \)を共に\( \ 1 \ \)とすることは禁止されている。
(2) \( \ \mathrm {JK – FF} \ \)においては,クロックパルスの動作タイミングで入力\( \ J \ \)と\( \ K \ \)がそれぞれ\( \ 1 \ \)と\( \ 0 \ \)の場合に\( \ 1 \ \)を,入力\( \ J \ \)と\( \ K \ \)がそれぞれ\( \ 0 \ \)と\( \ 1 \ \)の場合に\( \ 0 \ \)を出力し,入力\( \ J \ \)と\( \ K \ \)が共に\( \ 1 \ \)の場合には出力を保持する。
(3) \( \ \mathrm {T – FF} \ \)は,クロックパルスの動作タイミングにおいて,出力を反転する。
(4) \( \ \mathrm {D – FF} \ \)は,クロックパルスの動作タイミングにおいて,入力\( \ D \ \)と一致した出力を行う。
(5) \( \ \mathrm {FF} \ \)の用途として,カウンタ回路やレジスタ回路などがある。
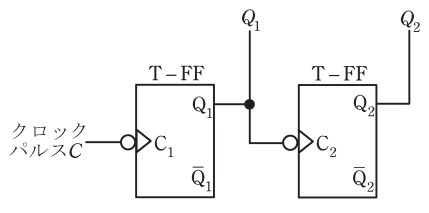
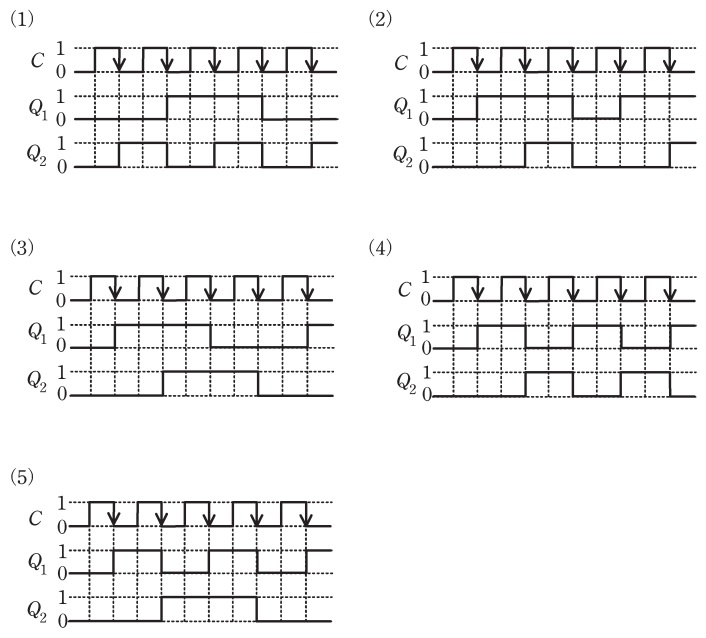
(b) クロックパルスの立ち下がりで動作する二つの\( \ \mathrm {T – FF} \ \)を用いた図の回路を考える。この回路において,クロックパルス\( \ C \ \)に対する回路の出力\( \ Q_{1} \ \)及び\( \ Q_{2} \ \)のタイムチャートとして,正しいものを次の(1)~(5)のうちから一つ選べ。
【ワンポイント解説】
フリップフロップに関する問題です。
学生時代に電子工学を習熟された方であれば比較的容易に解ける問題かもしれませんが,電験のテキストとしては掲載のほぼない分野となります。
出題されるとしても選択問題なので,勉強しない選択肢もありかと思います。
1.フリップフロップ
論理回路のうち出力を一時的に保持することができる記憶回路のことをいいます。
大学の電子工学では,細かな回路構成も勉強しますが,電験においてはその概要と真理値表を見ておけば十分かと思います。
①\( \ \mathrm {RS} \ \)フリップフロップ
図1に示すような回路構成で,フリップフロップとしては最も単純な回路となります。真理値表は表1のようになります。
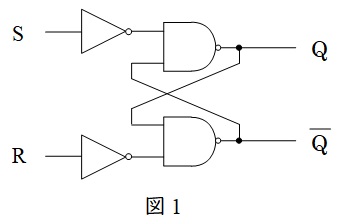
表 1
\[
\begin{array}{|c|c|c|c|}
\hline
\mathrm {S} & \mathrm {R} & \mathrm {Q} & \overline {\mathrm {Q}} \\
\hline
0 & 0 & 保持 & 保持 \\
0 & 1 & 0 & 1 \\
1 & 0 & 1 & 0 \\
1 & 1 & 禁止 & 禁止 \\
\hline
\end{array}
\]
②\( \ \mathrm {JK} \ \)フリップフロップ
回路は\( \ \mathrm {RS} \ \)フリップフロップに\( \ \mathrm {AND} \ \)回路を接続したような回路ですが,真理値表は表2のように\( \ \mathrm {RS} \ \)フリップフロップをベースとして,入力を共に\( \ 1 \ \)とした場合に出力が反転するフリップフロップとなります。
表 2
\[
\begin{array}{|c|c|c|c|}
\hline
\mathrm {J} & \mathrm {K} & \mathrm {Q} & \overline {\mathrm {Q}} \\
\hline
0 & 0 & 保持 & 保持 \\
0 & 1 & 0 & 1 \\
1 & 0 & 1 & 0 \\
1 & 1 & 反転 & 反転 \\
\hline
\end{array}
\]
③\( \ \mathrm {T} \ \)フリップフロップ
入力\( \ \mathrm {T} \ \)が\( \ 0 \ \)のとき出力を保持し,\( \ 1 \ \)のとき出力を反転するフリップフロップで,真理値表は表3のようになります。\( \ 0→1 \ \)の立ち上がり時や\( \ 1→0 \ \)の立ち下がり時のトリガにより動作するものもあります。
表 3
\[
\begin{array}{|c|c|c|}
\hline
\mathrm {T} & \mathrm {Q} & \overline {\mathrm {Q}} \\
\hline
0 & 保持 & 保持 \\
1 & 反転 & 反転 \\
\hline
\end{array}
\]
④\( \ \mathrm {D} \ \)フリップフロップ
入力が\( \ \mathrm {CLK} \ \)と\( \ \mathrm {D} \ \)があり,\( \ \mathrm {CLK} \ \)が\( \ 0 \ \)のとき出力を保持し,\( \ \mathrm {CLK} \ \)が\( \ 1 \ \)のとき\( \ \mathrm {D} \ \)を\( \ \mathrm {Q} \ \)に出力するフリップフロップで真理値表は表4のようになります。\( \ 0→1 \ \)の立ち上がり時や\( \ 1→0 \ \)の立ち下がり時のトリガにより動作するものもあります。
表 4
\[
\begin{array}{|c|c|c|c|}
\hline
\mathrm {CLK} & \mathrm {D} & \mathrm {Q} & \overline {\mathrm {Q}} \\
\hline
0 & 0 & 保持 & 保持 \\
0 & 1 & 保持 & 保持 \\
1 & 0 & 0 & 1 \\
1 & 1 & 1 & 0 \\
\hline
\end{array}
\]
【解答】
(a)解答:(2)
(1)正しい
ワンポイント解説「1.フリップフロップ」表1の通り,\( \ \mathrm {RS – FF} \ \)は,入力\( \ R \ \)と\( \ S \ \)が\( \ 1 \ \)と\( \ 0 \ \)の場合に\( \ 0 \ \),入力\( \ R \ \)と\( \ S \ \)が\( \ 0 \ \)と\( \ 1 \ \)の場合に\( \ 1 \ \)を出力します。また,入力\( \ R \ \)と\( \ S \ \)を共に\( \ 1 \ \)とすることは禁止されています。
(2)誤り
ワンポイント解説「1.フリップフロップ」表2の通り,\( \ \mathrm {JK – FF} \ \)は,入力\( \ J \ \)と\( \ K \ \)が\( \ 1 \ \)と\( \ 0 \ \)の場合に\( \ 1 \ \)を,入力\( \ J \ \)と\( \ K \ \)が\( \ 0 \ \)と\( \ 1 \ \)の場合に\( \ 0 \ \)を出力し,入力\( \ J \ \)と\( \ K \ \)が共に\( \ 1 \ \)の場合には出力を反転します。
(3)正しい
ワンポイント解説「1.フリップフロップ」表3の通り,\( \ \mathrm {T – FF} \ \)は,クロックパルスの動作タイミング(表3でいう入力が\( \ 1 \ \))において出力を反転します。
(4)正しい
ワンポイント解説「1.フリップフロップ」表4の通り,\( \ \mathrm {D – FF} \ \)は,クロックパルスの動作タイミング(表4でいう\( \ \mathrm {CLK} \ \)入力が\( \ 1 \ \))において,入力\( \ D \ \)と一致した出力を行います。
(5)正しい
\( \ \mathrm {FF} \ \)の用途として,カウントアップ等を自動的に行うカウンタ回路や一次記憶するレジスタ回路などがあります。
(b)解答:(5)
題意より,本問のフリップフロップはクロックパルスの立ち下がりで動作するので,\( \ C \ \)が立ち下がったタイミングで\( \ Q_{1} \ \)が反転し,\( \ Q_{1} \ \)が立ち下がったタイミングで\( \ Q_{2} \ \)が反転するタイムチャートが正しい。
\( \ C \ \)が立ち下がったタイミングで\( \ Q_{1} \ \)が反転しているのは(4)と(5)であり,このうち\( \ Q_{1} \ \)が立ち下がったタイミングで\( \ Q_{2} \ \)が反転しているのは(5)である。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは