《理論》〈電子理論〉[H18:問18]負帰還増幅回路の等価回路と電圧増幅度に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

図1のようなトランジスタ増幅回路がある。次の(a)及び(b)に答えよ。

ただし，\( \ R_{A} \ \)，\( \ R_{B} \ \)，\( \ R_{C} \ \)，\( \ R_{E} \ \)，\( \ R_{L} \ \)は抵抗，\( \ C_{1} \ \)，\( \ C_{2} \ \)，\( \ C_{3} \ \)はコンデンサ，\( \ V_{DD} \ \)は直流電圧源，\( \ v_{i} \ \)，\( \ v_{o} \ \)は交流信号電圧とする。

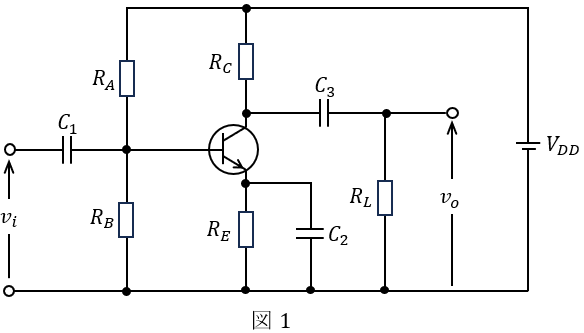
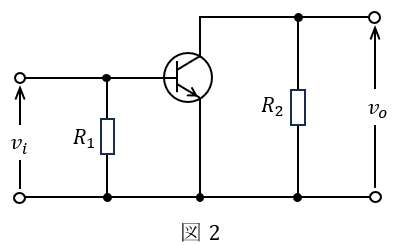
(a)　図1の回路を交流信号に注目し，交流回路として考える。この場合，この回路を図2のような等価な回路に置き換えることができる。このとき等価な抵抗\( \ R_{1} \ \)，\( \ R_{2} \ \)の値を表す式として，正しいのは次のうちどれか。

ただし，\( \ C_{1} \ \)，\( \ C_{2} \ \)，\( \ C_{3} \ \)のインピーダンスは十分小さく無視できるものとする。

\[
\begin{array}{ccc}
& R_{1} & R_{2} \\
\hline
(1) & 　\displaystyle \frac {R_{A}R_{B}}{R_{A}+R_{B}}　 & 　\displaystyle \frac {R_{C}R_{L}}{R_{C}+R_{L}}　 \\
\hline
(2) & 　\displaystyle \frac {R_{B}R_{E}}{R_{B}+R_{E}}　 & 　\displaystyle \frac {R_{A}R_{C}}{R_{A}+R_{C}}　 \\
\hline
(3) & 　\displaystyle \frac {R_{B}R_{E}}{R_{B}+R_{E}}　 & 　\displaystyle \frac {R_{C}R_{L}}{R_{C}+R_{L}}　 \\
\hline
(4) & 　\displaystyle \frac {R_{A}R_{C}}{R_{A}+R_{C}}　 & 　\displaystyle \frac {R_{E}R_{L}}{R_{E}+R_{L}}　 \\
\hline
(5) & 　\displaystyle \frac {R_{A}R_{B}}{R_{A}+R_{B}}　 & 　\displaystyle \frac {R_{E}R_{L}}{R_{E}+R_{L}}　 \\
\hline
\end{array}
\]

(b)　図2の回路で，トランジスタの入力インピーダンス\( \ h_{ie}=6 \ \mathrm {[k\Omega ]} \ \)，電流増幅率\( \ h_{fe}=140 \ \)であった。この回路の電圧増幅度の大きさとして，最も近いのは次のうちどれか。

ただし，図1の回路において，各抵抗は\( \ R_{A}=100 \ \mathrm {[k\Omega ]} \ \)，\( \ R_{B}=25 \ \mathrm {[k\Omega ]} \ \)，\( \ R_{C}=8 \ \mathrm {[k\Omega ]} \ \)，\( \ R_{E}=2.2 \ \mathrm {[k\Omega ]} \ \)，\( \ R_{L}=15 \ \mathrm {[k\Omega ]} \ \)とし，出力アドミタンス\( \ h_{oe} \ \)及び電圧帰還率\( \ h_{re} \ \)は無視できるものとする。

　(1)　\( \ 15.7 \ \)　　(2)　\( \ 82 \ \)　　(3)　\( \ 122 \ \)　　(4)　\( \ 447 \ \)　　(5)　\( \ 753 \ \)

【ワンポイント解説】

負帰還増幅回路の等価回路と電圧増幅度を求める問題です。
小信号等価回路は与えられる場合が多いですが，本問は与えられていないので，自分で描いて解いていく必要がある難問です。
(a)は電気回路等でも役立つ知識となるので，(a)を優先にマスターしておくようにして下さい。

1.バイポーラトランジスタの小信号等価回路
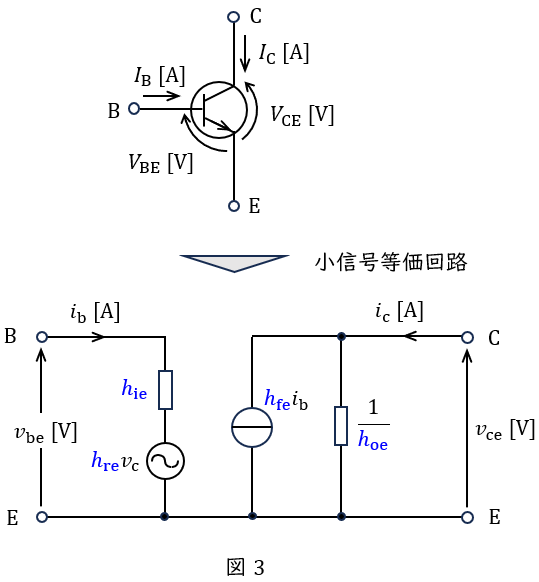
エミッタ接地におけるバイポーラトランジスタの交流信号分に着目した小信号等価回路は図3のように描けます。入出力信号の関係を式で表すと，
\[
\begin{eqnarray}
v_{\mathrm {b}}&=&h_{\mathrm {ie}}i_{\mathrm {b}}+h_{\mathrm {re}}v_{\mathrm {c}} \\[ 5pt ] i_{\mathrm {c}}&=&h_{\mathrm {fe}}i_{\mathrm {b}}+h_{\mathrm {oe}}v_{\mathrm {c}} \\[ 5pt ] \end{eqnarray}
\] となりまず。ただし，\( \ h_{\mathrm {ie}} \ \)，\( \ h_{\mathrm {re}} \ \)，\( \ h_{\mathrm {fe}} \ \)，\( \ h_{\mathrm {oe}} \ \)を\( \ h \ \)パラメータといい，
　\( \ h_{\mathrm {ie}} \ \)：入力インピーダンス\( \ \mathrm {[\Omega]} \ \)
　\( \ h_{\mathrm {re}} \ \)：電圧帰還率
　\( \ h_{\mathrm {fe}} \ \)：電流増幅率
　\( \ h_{\mathrm {oe}} \ \)：出力アドミタンス
といいます。ただし，\( \ h_{\mathrm {re}} \ \)及び\( \ h_{\mathrm {oe}} \ \)は非常に小さい値ということで無視する場合が多いです。

【解答】

(a)解答：(1)
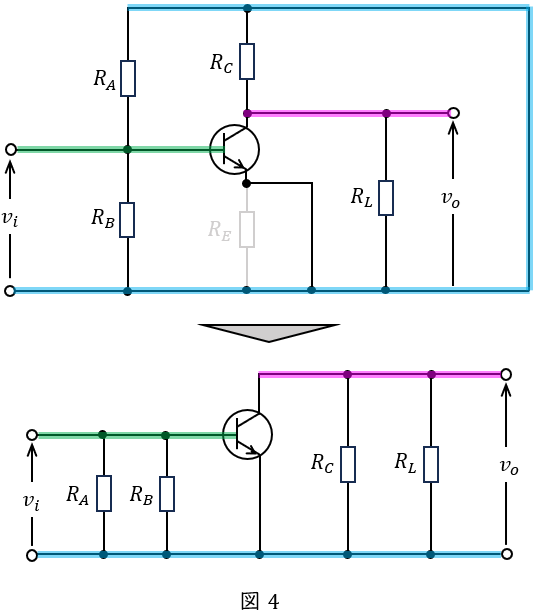
題意の通り，\( \ C_{1} \ \)，\( \ C_{2} \ \)，\( \ C_{3} \ \)のインピーダンスは十分小さく無視できるので，交流信号分について整理すると図4のようになる。
したがって，図4と図2を比較すると，\( \ R_{1} \ \)は\( \ R_{A} \ \)と\( \ R_{B} \ \)の並列合成抵抗，\( \ R_{2} \ \)は\( \ R_{C} \ \)と\( \ R_{L} \ \)の並列合成抵抗であるので，
\[
\begin{eqnarray}
R_{1}&=&\frac {R_{A}R_{B}}{R_{A}+R_{B}} \\[ 5pt ] R_{2}&=&\frac {R_{C}R_{L}}{R_{C}+R_{L}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(3)
(a)より，\( \ R_{1} \ \mathrm {[k\Omega ]} \ \)及び\( \ R_{2} \ \mathrm {[k\Omega ]} \ \)の大きさは，
\[
\begin{eqnarray}
R_{1}&=&\frac {R_{A}R_{B}}{R_{A}+R_{B}} \\[ 5pt ] &=&\frac {100\times 25}{100+25} \\[ 5pt ] &=&20 \ \mathrm {[k\Omega ]} \\[ 5pt ] R_{2}&=&\frac {R_{C}R_{L}}{R_{C}+R_{L}} \\[ 5pt ] &=&\frac {8\times 15}{8+15} \\[ 5pt ] &≒&5.217 \ \mathrm {[k\Omega ]} \\[ 5pt ] \end{eqnarray}
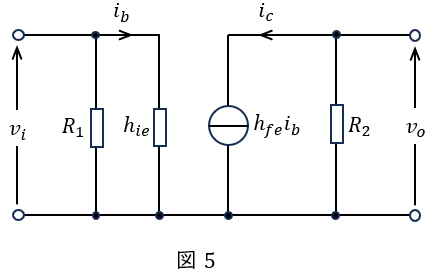
\] となり，ワンポイント解説「1.バイポーラトランジスタの小信号等価回路」に沿って等価回路を描くと図5のようになる。図5より，電圧増幅度\( \ \displaystyle \left| \frac {v_{o}}{v_{i}}\right| \ \)は，
\[
\begin{eqnarray}
\left| \frac {v_{o}}{v_{i}}\right| &=&\left| \frac {-R_{2}h_{fe}i_{b}}{h_{ie}i_{b}}\right| \\[ 5pt ] &=& \frac {R_{2}h_{fe}}{h_{ie}} \\[ 5pt ] &=& \frac {5.217\times 10^{3}\times 140}{6\times 10^{3}} \\[ 5pt ] &≒&122 \\[ 5pt ] \end{eqnarray}
\] と求められる。