《電力》〈配電〉[H26:問12]三相4線式低圧配電線の容量に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

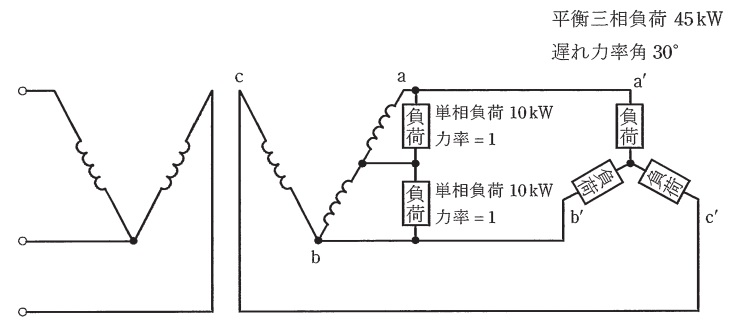
図のように，2台の単相変圧器による電灯動力共用の三相4線式低圧配電線に，平衡三相負荷\(45 \ \mathrm {kW}\)(遅れ力率角\(30°\))1個及び単相負荷\(10 \ \mathrm {kW}\)(力率\(=1\))2個が接続されている。これに供給するための共用変圧器及び専用変圧器の容量の値\(\mathrm {[kV\cdot A]}\)は，それぞれいくら以上でなければならないか。値の組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。

ただし，相回転は\(\mathrm {a}^{\prime }－\mathrm {c}^{\prime }－\mathrm {b}^{\prime }\)とする。

【ワンポイント解説】

三相4線式の低圧配電線に関する問題です。初見ではかなり難しい問題となりますが，ある程度パターン化される問題なので，過去問を何度か解いて確実に解けるようにしましょう。

1.三相4線式低圧配電線
問題図において，単相変圧器\(\mathrm {a}－\mathrm {b}\)は単相負荷と三相負荷両方へ供給するので共用変圧器，単相変圧器\(\mathrm {b}－\mathrm {c}\)は三相負荷のみに供給するので，専用変圧器と言います。

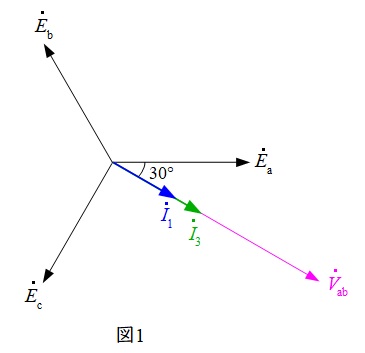
単相負荷は線間電圧\(V_{\mathrm {ab}}\)から供給されるので，その力率は線間電圧\(V_{\mathrm {ab}}\)と単相負荷へ流れる電流\(I_{1}\)との位相差となります。一方，三相負荷はそれぞれの相電圧と相電流の位相差になります。よって，ベクトル図は図1のように描くことができ，\(I_{1}\)と\(a^{\prime }\)に流れる電流\(I_{3}\)は同相となります。

【関連する「電気の神髄」記事】

　　中性点接地方式の種類と特徴

【解答】

解答：(5)
図1のベクトル図より，単相負荷2個にかかる電力は力率が1であるから，
\[
V_{\mathrm {ab}}I_{1}=20 \ \mathrm {[kW ]}
\] となる。一方，三相負荷にかかる電力から，
\[
\begin{eqnarray}
\sqrt {3}V_{\mathrm {ab}}I_{3}\cos 30°&=&45 \\[ 5pt ] \sqrt {3}V_{\mathrm {ab}}I_{3}\frac {\sqrt {3}}{2}&=&45 \\[ 5pt ] V_{\mathrm {ab}}I_{3}&=&30 \ \mathrm {[kV\cdot A ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。よって，共通変圧器に流れる電流は\(I_{1}+I_{3}\)，専用変圧器に流れる電流は\(I_{3}\)であるから，共通変圧器の容量は，
\[
\begin{eqnarray}
V_{\mathrm {ab}}\left( I_{1}+I_{3}\right) &=&20+30 \\[ 5pt ] &=&50 \ \mathrm {[kV\cdot A]} \\[ 5pt ] \end{eqnarray}
\] と求められ，専用変圧器の容量は，
\[
\begin{eqnarray}
V_{\mathrm {bc}}I_{3} &=&V_{\mathrm {ab}}I_{3} \\[ 5pt ] &=&30 \ \mathrm {[kV\cdot A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。