《電力》〈送電〉[H24:問16]π形等価回路の回路計算に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

三相\( \ 3 \ \)線式\( \ 1 \ \)回線無負荷送電線の送電端に線間電圧\( \ 66.0 \ \mathrm {[kV]} \ \)を加えると，受電端の線間電圧は\( \ 72.0 \ \mathrm {[kV]} \ \)，\( \ 1 \ \)線当たりの送電端電流は\( \ 30.0 \ \mathrm {[A]} \ \)であった。この送電線が，線路アドミタンス\( \ B \ \mathrm {[mS]} \ \)と線路リアクタンス\( \ X \ \mathrm {[\Omega ]} \ \)を用いて，図に示す等価回路で表現できるとき，次の(a)及び(b)の問に答えよ。

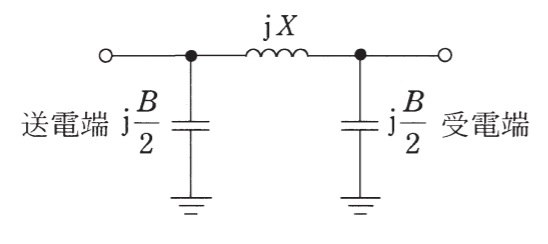
(a)　線路アドミタンス\( \ B \ \mathrm {[mS]} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 0.217 \ \)　　(2)　\( \ 0.377 \ \)　　(3)　\( \ 0.435 \ \)　　(4)　\( \ 0.545 \ \)　　(5)　\( \ 0.753 \ \)

(b)　線路リアクタンス\( \ X \ \mathrm {[\Omega ]} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 222 \ \)　　(2)　\( \ 306 \ \)　　(3)　\( \ 384 \ \)　　(4)　\( \ 443 \ \)　　(5)　\( \ 770 \ \)

【ワンポイント解説】

\( \ \pi \ \)形等価回路からの出題です。内容としては２種以上で出題されるような内容で，令和元年にも出題されていますが，３種受験生としては厳しい問題であったかもしれません。ある程度パターン化されるような内容なので，理解できれば合格に大きく近づくと思います。

【解答】

(a)解答：(5)
問題図の\( \ \pi \ \)形等価回路において，送電端電圧(相電圧)を\( \ {\dot E}_{\mathrm {s}} \ \)，受電端電圧(相電圧)を\( \ {\dot E}_{\mathrm {r}} \ \)，送電端側のアドミタンスに流れる電流を\( \ {\dot I}_{1} \ \)，受電端側のアドミタンスに流れる電流を\( \ {\dot I}_{2} \ \)とする。
\[
\begin{eqnarray}
{\dot I}_{2} &=&\mathrm {j}\frac {B}{2}{\dot E}_{\mathrm {r}} \\[ 5pt ] \end{eqnarray}
\] であり，受電端は無負荷であるから，送電端電圧\( \ {\dot E}_{\mathrm {s}} \ \)は，
\[
\begin{eqnarray}
{\dot E}_{\mathrm {s}} &=&{\dot E}_{\mathrm {r}}+\mathrm {j}X{\dot I}_{2} \\[ 5pt ] &=&{\dot E}_{\mathrm {r}}+\mathrm {j}X\left( \mathrm {j}\frac {B}{2}{\dot E}_{\mathrm {r}}\right) \\[ 5pt ] &=&{\dot E}_{\mathrm {r}}-\frac {XB}{2}{\dot E}_{\mathrm {r}} \\[ 5pt ] &=&\left( 1-\frac {XB}{2}\right) {\dot E}_{\mathrm {r}} \\[ 5pt ] \end{eqnarray}
\] となる。上式より，\( \ {\dot E}_{\mathrm {s}} \ \)と\( \ {\dot E}_{\mathrm {r}} \ \)は同相であることが分かる。送電端については，
\[
\begin{eqnarray}
{\dot I}_{1} &=&\mathrm {j}\frac {B}{2}{\dot E}_{\mathrm {s}} \\[ 5pt ] \end{eqnarray}
\] であり，送電端電流\( \ {\dot I}_{\mathrm {s}} \ \)は，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {s}} &=&{\dot I}_{1}+{\dot I}_{2} \\[ 5pt ] &=&\mathrm {j}\frac {B}{2}{\dot E}_{\mathrm {s}}+\mathrm {j}\frac {B}{2}{\dot E}_{\mathrm {r}}\\[ 5pt ] &=&\mathrm {j}\frac {B}{2}\left( {\dot E}_{\mathrm {s}}+{\dot E}_{\mathrm {r}} \right) \\[ 5pt ] \end{eqnarray}
\] となるので，両辺絶対値を取り，各値を代入すると，
\[
\begin{eqnarray}
\left| {\dot I}_{\mathrm {s}}\right| &=&\left| \mathrm {j}\frac {B}{2}\left( {\dot E}_{\mathrm {s}}+{\dot E}_{\mathrm {r}} \right) \right| \\[ 5pt ] \left| {\dot I}_{\mathrm {s}}\right| &=&\frac {B}{2}\left( \left| {\dot E}_{\mathrm {s}}\right| +\left| {\dot E}_{\mathrm {r}}\right| \right) \\[ 5pt ] 30&=&\frac {B}{2}\left( \frac {66000}{\sqrt {3}}+\frac {72000}{\sqrt {3}} \right) \\[ 5pt ] B&=&\frac {30\times 2\times \sqrt {3}}{66000+72000} \\[ 5pt ] &≒&0.7531\times 10^{-3} \ \mathrm {[S]}　→ 0.753 \ \mathrm {[mS]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(1)
\[
\begin{eqnarray}
{\dot E}_{\mathrm {s}} &=&\left( 1-\frac {XB}{2}\right) {\dot E}_{\mathrm {r}} \\[ 5pt ] \end{eqnarray}
\] の関係があるので，各値を代入すると，
\[
\begin{eqnarray}
\frac {66000}{\sqrt {3}} &=&\left( 1-\frac {X\times 0.7531\times 10^{-3}}{2}\right) \times \frac {72000}{\sqrt {3}} \\[ 5pt ] 66000 &=&\left( 1-\frac {X\times 0.7531\times 10^{-3}}{2}\right) \times 72000 \\[ 5pt ] 1-\frac {X\times 0.7531\times 10^{-3}}{2}&=&\frac {66000}{72000} \\[ 5pt ] \frac {X\times 0.7531\times 10^{-3}}{2}&=&1-\frac {66000}{72000} \\[ 5pt ] X&=&\frac {2}{0.7531\times 10^{-3}}\times \left( 1-\frac {66000}{72000}\right) \\[ 5pt ] &≒&221 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。