《機械》〈電動機応用〉[H25:問10]はずみ車に蓄えられる運動エネルギーに関する空欄穴埋問題

【問題】

【難易度】★★☆☆☆（やや易しい）

電動機ではずみ車を加速して，運動エネルギーを蓄えることを考える。

まず，加速するための電動機のトルクを考える。加速途中の電動機の回転速度を\( \ N \ \mathrm {[{min}^{-1}]} \ \)とすると，そのときの毎秒の回転速度\( \ n \ \mathrm {[s^{-1}]} \ \)は①式で表される。
\[
\begin{eqnarray}
\fbox {　 （ア） 　}　・・・・・・・・・・・・・・・・・　① \\[ 5pt ] \end{eqnarray}
\] この回転速度\( \ n \ \mathrm {[s^{-1}]} \ \)から②式で角速度\( \ \omega \ \mathrm {[rad／s]} \ \)を求めることができる。
\[
\begin{eqnarray}
\fbox {　 （イ） 　}　・・・・・・・・・・・・・・・・・　② \\[ 5pt ] \end{eqnarray}
\] このときの電動機が\( \ 1 \ \)秒間にする仕事，すなわち出力を\( \ P \ \mathrm {[W]} \ \)とすると，トルク\( \ T \ \mathrm {[N\cdot m]} \ \)は③式となる。
\[
\begin{eqnarray}
\fbox {　 （ウ） 　}　・・・・・・・・・・・・・・・・・　③ \\[ 5pt ] \end{eqnarray}
\] ③式のトルクによってはずみ車を加速する。電動機が出力し続けて加速している間，この分のエネルギーがはずみ車に注入される。電動機に直結するはずみ車の慣性モーメントを\( \ I \ \mathrm {[kg\cdot m^{2}]} \ \)として，加速が完了したときの電動機の角速度を\( \ \omega _{0} \ \mathrm {[rad／s]} \ \)とすると，このはずみ車に蓄えられている運動エネルギー\( \ E \ \mathrm {[J]} \ \)は④式となる。
\[
\begin{eqnarray}
\fbox {　 （エ） 　}　・・・・・・・・・・・・・・・・・　④ \\[ 5pt ] \end{eqnarray}
\] 上記の記述中の空白箇所(ア)，(イ)，(ウ)及び(エ)に当てはまる組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。
\[
\begin{array}{ccccc}
& （ア） & （イ） & （ウ） & （エ） \\
\hline
(1) & 　n=\displaystyle \frac {N}{60}　 & 　\omega =2\pi \times n　 & 　T=\displaystyle \frac {P}{\omega }　 & 　E=\displaystyle \frac {1}{2}I^{2}\omega _{0}　 \\
\hline
(2) & 　n=60N　 & 　\omega =\displaystyle \frac {n}{2\pi }　 & 　T=P\omega　 & 　E=\displaystyle \frac {1}{2}I^{2}\omega _{0}　 \\
\hline
(3) & 　n=\displaystyle \frac {N}{60}　 & 　\omega =2\pi \times n　 & 　T=P\omega　 & 　E=\displaystyle \frac {1}{2}I\omega _{0}^{2}　 \\
\hline
(4) & 　n=60N　 & 　\omega =\displaystyle \frac {n}{2\pi }　 & 　T=\displaystyle \frac {P}{\omega }　 & 　E=\displaystyle \frac {1}{2}I^{2}\omega _{0}　 \\
\hline
(5) & 　n=\displaystyle \frac {N}{60}　 & 　\omega =2\pi \times n　 & 　T=\displaystyle \frac {P}{\omega }　 & 　E=\displaystyle \frac {1}{2}I\omega _{0}^{2}　 \\
\hline
\end{array}
\]

【ワンポイント解説】

空欄になっている式はいずれも電動機の基本公式です。途中の導出過程を理解しておくことも大事ですが，試験本番では即答できるぐらいに習熟しておいた方が良いレベルの問題であると思います。

1.出力\( \ P \ \)とトルク\( \ T \ \)の関係
一般に電動機の出力\( \ P \ \mathrm {[W]} \ \)とトルク\( \ T \ \mathrm {[N\cdot m]} \ \)には，角速度\( \ \omega \ \mathrm {[rad／s]} \ \)であるとき，
\[
\begin{eqnarray}
P &=& \omega T \\[ 5pt ] \end{eqnarray}
\] の関係があります。

2.慣性モーメント\( \ J \ \)
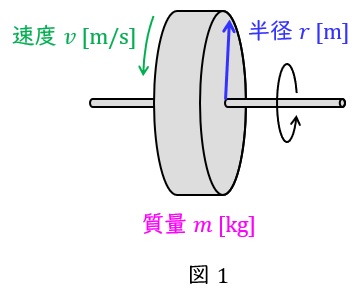
質量\( \ m \ \mathrm {[kg]} \ \)，速度\( \ v \ \mathrm {[m/s]} \ \)で回転している回転体の運動エネルギー\( \ W \ \mathrm {[J]} \ \)は，
\[
\begin{eqnarray}
W &=& \frac {1}{2}mv^{2} \\[ 5pt ] \end{eqnarray}
\] であり，回転体の半径を\( \ r \ \mathrm {[m]} \ \)，角速度を\( \ \omega \ \mathrm {[rad/s]} \ \)とすると，\( \ v=r\omega \ \)の関係があるから，
\[
\begin{eqnarray}
W &=& \frac {1}{2}m\left( r\omega \right) ^{2} \\[ 5pt ] &=& \frac {1}{2}mr^{2}\omega ^{2} \\[ 5pt ] &=& \frac {1}{2}J\omega ^{2} \\[ 5pt ] \end{eqnarray}
\] となります。この\( \ J=mr ^{2} \ \)を慣性モーメントと呼びます。
慣性モーメントが大きいと，回転体は加速しにくく，減速しにくいという特徴があります。

【解答】

解答：(5)
(ア)
\( \ N \ \mathrm {[{min}^{-1}]} \ \)は毎分の回転速度，\( \ n \ \mathrm {[s^{-1}]} \ \)は毎秒の回転速度であるので，\( \ \displaystyle n=\frac {N}{60} \ \)となります。

(イ)
１回転あたりの弧度は\( \ 2\pi \ \)なので，角速度\( \ \omega \ \mathrm {[rad／s]} \ \)は，\( \ \omega =2\pi n \ \)となります。\( \ \displaystyle \omega =\frac {2\pi N}{60} \ \)も非常によく使う公式なので，暗記しておくようにしましょう。

(ウ)
\( \ P=\omega T \ \)の関係より，\( \ \displaystyle T =\frac {P}{\omega } \ \)となります。

(エ)
はずみ車が回転している時の運動エネルギー\( \ E \ \mathrm {[J]} \ \)は，はずみ車の重量を\( \ m \ \mathrm {[kg]} \ \)，半径を\( \ r \ \mathrm {[m]} \ \)，速度を\( \ v=r\omega _{0} \)とすると，
\[
\begin{eqnarray}
E&=&\frac {1}{2}mv^{2} \\[ 5pt ] &=&\frac {1}{2}mr^{2}\omega _{0} ^{2} \\[ 5pt ] \end{eqnarray}
\] であり，慣性モーメント\( \ I=mr^{2} \)であるから，
\[
\begin{eqnarray}
E&=&\frac {1}{2}I\omega _{0} ^{2} \\[ 5pt ] \end{eqnarray}
\] と求められる。