《機械》〈パワーエレクトロニクス〉[H28:問9]直流チョッパに関する計算問題

【問題】

【難易度】★★★☆☆（普通）

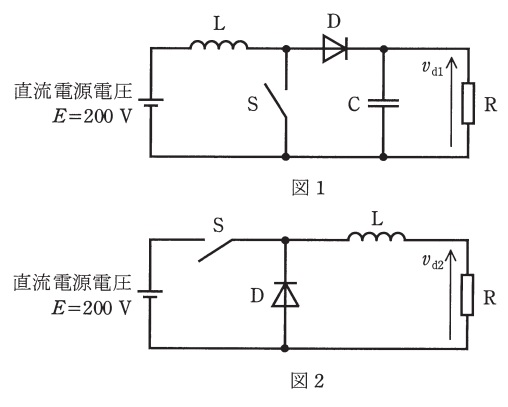
図は2種類の直流チョッパを示している。いずれの回路もスイッチ\( \ \mathrm {S} \ \)，ダイオード\( \ \mathrm {D} \ \)，リアクトル\( \ \mathrm {L} \ \)，コンデンサ\( \ \mathrm {C} \ \) ( 図1のみに使用されている。 ) を用いて，直流電源電圧\( \ E=200 \ \mathrm {V} \ \)を変換し，負荷抵抗\( \ \mathrm {R} \ \)の電圧\( \ v_{\mathrm {d1}} \ \)，\( \ v_{\mathrm {d2}} \ \)を制御するためのものである。これらの回路で，直流電源電圧は\( \ E=200 \ \mathrm {V} \ \)一定とする。また，負荷抵抗\( \ \mathrm {R} \ \)の抵抗値とリアクトル\( \ \mathrm {L} \ \)のインダクタンス又はコンデンサ\( \ \mathrm {C} \ \) の静電容量の値とで決まる時定数が，スイッチ\( \ \mathrm {S} \ \)の動作周期に対して十分に大きいものとする。各回路のスイッチ\( \ \mathrm {S} \ \)の通流率を\( \ \mathrm {0.7} \ \)とした場合，負荷抵抗\( \ \mathrm {R} \ \)の電圧\( \ v_{\mathrm {d1}} \ \)，\( \ v_{\mathrm {d2}} \ \)の平均値\( \ V_{\mathrm {d1}} \ \)，\( \ V_{\mathrm {d2}} \ \)の値\( \ \mathrm {[ V ]} \ \)の組合せとして，最も近いものを次の(1)～(5)のうちから一つ選べ。

\[
\begin{array}{ccc}
& V_{\mathrm {d1}} & V_{\mathrm {d2}} \\
\hline
(1) & 667 & 140 \\
\hline
(2) & 467 & 60 \\
\hline
(3) & 667 & 86 \\
\hline
(4) & 467 & 140 \\
\hline
(5) & 286 & 60 \\
\hline
\end{array}
\]

【ワンポイント解説】

図1が昇圧チョッパ，図2が降圧チョッパとなります。公式を暗記していれば，原理を考えずとも解けてしまいます。通常はスイッチではなく，トランジスタを用いることが多いです。

1.降圧チョッパ
平滑リアクトルがない時は，スイッチ\( \ \mathrm {ON} \ \)時は\( \ 200 \ \mathrm {V} \ \)，スイッチ\( \ \mathrm {OFF} \ \)時は\( \ 0 \ \mathrm {V} \ \)となりますが，平滑リアクトルに蓄えられるエネルギーにより，一定電圧(平均電圧)を出力することができます。よって，図2の場合では，
\[
\begin{eqnarray}
V_{\mathrm {d2}}&=&\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}E \\[ 5pt ] \end{eqnarray}
\] となります。

2.昇圧チョッパ
スイッチ\( \ \mathrm {S} \ \)が\( \ \mathrm {ON} \ \)時はリアクトル\( \ \mathrm {L} \ \)にエネルギー\( \ EIT_{\mathrm {on}} \ \)が蓄えられ，スイッチ\( \ \mathrm {OFF} \ \)時はリアクトル\( \ \mathrm {L} \ \)に蓄えられたエネルギー\( \ \displaystyle L\frac {di}{dt}IT_{\mathrm {off}} \ \)が放出されます。定常状態では蓄えられるエネルギーと放出するエネルギーが等しいので，
\[
\begin{eqnarray}
EIT_{\mathrm {on}}&=&L\frac {di}{dt}IT_{\mathrm {off}} \\[ 5pt ] ET_{\mathrm {on}}&=&L\frac {di}{dt}T_{\mathrm {off}} \\[ 5pt ] L\frac {di}{dt}&=&\frac {T_{\mathrm {on}}}{T_{\mathrm {off}}}E \\[ 5pt ] \end{eqnarray}
\] となります。また回路方程式は，
\[
\begin{eqnarray}
E+L\frac {di}{dt}&=&v_{d1} \\[ 5pt ] \end{eqnarray}
\] となるので，
\[
\begin{eqnarray}
E+L\frac {di}{dt}&=&v_{\mathrm {d1}} \\[ 5pt ] E+\frac {T_{\mathrm {on}}}{T_{\mathrm {off}}}E&=&v_{\mathrm {d1}} \\[ 5pt ] v_{\mathrm {d1}}&=&\frac {T_{\mathrm {on}}+T_{\mathrm {off}}}{T_{\mathrm {off}}}E \\[ 5pt ] \end{eqnarray}
\] となります。

【関連する「電気の神髄」記事】

　　降圧チョッパ回路の理論
　　昇圧チョッパ回路の理論

【解答】

解答：(1)
図1は昇圧チョッパであるから，
\[
\begin{eqnarray}
V_{\mathrm {d1}}&=&\frac {T_{\mathrm {on}}+T_{\mathrm {off}}}{T_{\mathrm {off}}}E \\[ 5pt ] &=& \frac {1}{0.3}\times 200\\[ 5pt ] &≒&667 \ \mathrm {[ V ]} \\[ 5pt ] \end{eqnarray}
\] となる。一方，図2は降圧チョッパであるから，
\[
\begin{eqnarray}
V_{\mathrm {d2}}&=&\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}E \\[ 5pt ] &=& \frac {0.7}{1}\times 200\\[ 5pt ] &=&140 \ \mathrm {[ V ]} \\[ 5pt ] \end{eqnarray}
\] となる。