《機械》〈自動制御〉[H25:問13]フィードバック制御の伝達関数に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

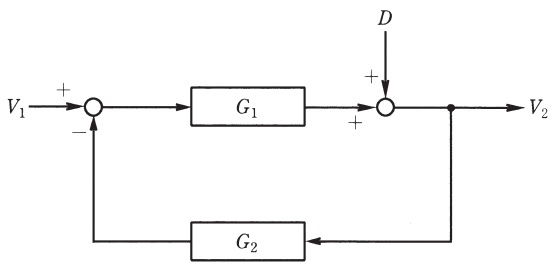
図は，フィードバック制御におけるブロック線図を示している。この線図において，出力\( \ V_{2} \ \)を，入力\( \ V_{1} \ \)及び外乱\( \ D \ \)を使って表現した場合，正しいものを次の(1)～(5)のうちから一つ選べ。

\[
\begin{eqnarray}
(1)　V_{2}=\frac {1}{1+G_{1}G_{2}}V_{1}+\frac {G_{2}}{1+G_{1}G_{2}}D \\[ 5pt ] (2)　V_{2}=\frac {G_{2}}{1+G_{1}G_{2}}V_{1}+\frac {1}{1+G_{1}G_{2}}D \\[ 5pt ] (3)　V_{2}=\frac {G_{2}}{1+G_{1}G_{2}}V_{1}-\frac {1}{1+G_{1}G_{2}}D \\[ 5pt ] (4)　V_{2}=\frac {G_{1}}{1+G_{1}G_{2}}V_{1}-\frac {1}{1+G_{1}G_{2}}D \\[ 5pt ] (5)　V_{2}=\frac {G_{1}}{1+G_{1}G_{2}}V_{1}+\frac {1}{1+G_{1}G_{2}}D \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

ブロック線図を等価変換をする方法と，ブロック線図の関係式から導き出す方法があり，どちらで解いても良いですが，私個人的には関係式の方が好きです。ここでは関係式を用いて解く方法で解説します。

【解答】

解答：(5)
ブロック線図より，
\[
\begin{eqnarray}
D+\left( V_{1}-G_{2}V_{2}\right) G_{1}&=&V_{2} \\[ 5pt ] \end{eqnarray}
\] の関係があるので，上式を\( \ V_{2} \ \)について解くと，
\[
\begin{eqnarray}
D+G_{1}V_{1}-G_{1}G_{2}V_{2}&=&V_{2} \\[ 5pt ] V_{2}+G_{1}G_{2}V_{2}&=&G_{1}V_{1}+D \\[ 5pt ] \left( 1+G_{1}G_{2}\right) V_{2}&=&G_{1}V_{1}+D \\[ 5pt ] V_{2}&=&\frac {G_{1}}{1+G_{1}G_{2}}V_{1}+\frac {1}{1+G_{1}G_{2}}D \\[ 5pt ] \end{eqnarray}
\] と求められる。