《機械》〈パワーエレクトロニクス〉[H25:問16]PWM制御に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

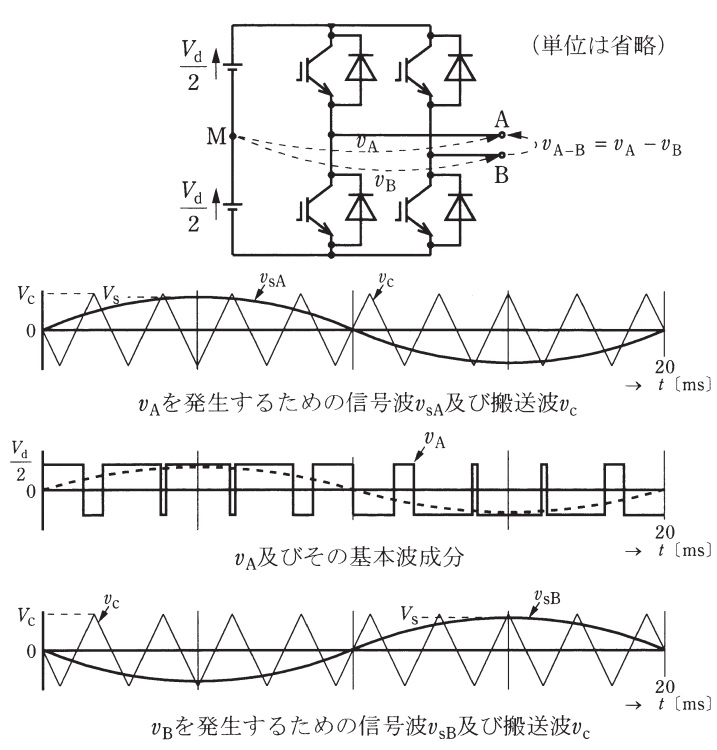
図は，パルス幅変調制御(\( \ \mathrm {PWM} \ \)制御)によって\( \ 50 \ \mathrm {[Hz]} \ \)の交流電圧を出力するインバータの回路及びその各部電圧波形である。直流の中点\( \ \mathrm {M} \ \)からみて端子\( \ \mathrm {A} \ \)及び\( \ \mathrm {B} \ \)に発生する瞬時電圧をそれぞれ\( \ v_{\mathrm {A}} \ \mathrm {[V]} \ \)及び\( \ v_{\mathrm {B}} \ \mathrm {[V]} \ \)とする。端子\( \ \mathrm {A} \ \)と\( \ \mathrm {B} \ \)との間の電圧\( \ v_{\mathrm {A-B}}=v_{\mathrm {A}}-v_{\mathrm {B}} \ \mathrm {[V]} \ \)に関する次の(a)及び(b)の問に答えよ。

(a)　\( \ v_{\mathrm {A}} \ \mathrm {[V]} \ \)及び\( \ v_{\mathrm {B}} \ \mathrm {[V]} \ \)の\( \ 50 \ \mathrm {[Hz]} \ \)の基本波成分の振幅\( \ V_{\mathrm {A}} \ \mathrm {[V]} \ \)及び\( \ V_{\mathrm {B}} \ \mathrm {[V]} \ \)は，それぞれ\( \ \displaystyle \frac {V_{\mathrm {s}}}{V_{\mathrm {c}}}\times \frac {V_{\mathrm {d}}}{2} \ \mathrm {[V]} \ \)で求められる。ここで，\( \ V_{\mathrm {c}} \ \mathrm {[V]} \ \)は搬送波(三角波)\( \ v_{\mathrm {c}} \ \mathrm {[V]} \ \)の振幅で\( \ 10 \ \mathrm {[V]} \ \)，\( \ V_{\mathrm {s}} \ \mathrm {[V]} \ \)は信号波(正弦波)\( \ v_{\mathrm {sA}} \ \mathrm {[V]} \ \)及び\( \ v_{\mathrm {sB}} \ \mathrm {[V]} \ \)の振幅で\( \ 9 \ \mathrm {[V]} \ \)，\( \ V_{\mathrm {d}} \ \mathrm {[V]} \ \)は直流電圧\( \ 200 \ \mathrm {[V]} \ \)である。\( \ v_{\mathrm {A-B}} \ \mathrm {[V]} \ \)の\( \ 50 \ \mathrm {[Hz]} \ \)基本波成分の振幅は\( \ V_{\mathrm {A-B}}=V_{\mathrm {A}}+V_{\mathrm {B}} \ \mathrm {[V]} \ \)となる。\( \ v_{\mathrm {A-B}} \ \mathrm {[V]} \ \)の基本波成分の実効値\( \ \mathrm {[V]} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\(64\)　　(2)　\(90\)　　(3)　\(127\)　　(4)　\(141\)　　(5)　\(156\)

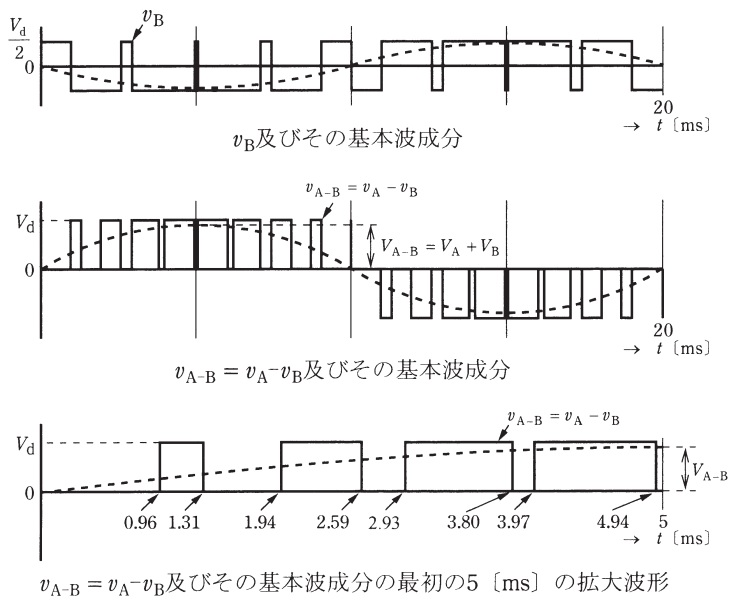
(b)　\( \ v_{\mathrm {A-B}} \ \mathrm {[V]} \ \)は，高調波を含んでいるため，高調波も含めた実効値\( \ V_{\mathrm {rms}} \ \mathrm {[V]} \ \)は，小問(a)で求めた基本波成分の実効値よりも大きい。波形が\( \ 5 \ \mathrm {[ms]} \ \)ごとに対称なので，実効値は最初の\( \ 5 \ \mathrm {[ms]} \ \)の区間で求めればよい。\( \ 5 \ \mathrm {[ms]} \ \)の区間で電圧を出力している時間の合計値を\( \ T_{\mathrm {s}} \ \mathrm {[ms]} \ \)とすると，実効値\( \ V_{\mathrm {rms}} \ \mathrm {[V]} \ \)は次の式で求められる。
\[
\begin{eqnarray}
V_{\mathrm {rms}} &=& \sqrt {\frac {T_{\mathrm {s}}}{5}\times V_{\mathrm {d}}^{2}}= \sqrt {\frac {T_{\mathrm {s}}}{5}}\times V_{\mathrm {d}} \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] 実効値\( \ V_{\mathrm {rms}} \ \mathrm {[V]} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\(88\)　　(2)　\(127\)　　(3)　\(141\)　　(4)　\(151\)　　(5)　\(163\)

【ワンポイント解説】

どちらかというと\( \ \mathrm {PWM} \ \)制御の中身を問うというよりも，文章の読解力がメインの問題です。何とも言えないですが，こういう問題であるとおそらく正答率は下がり点数差がついてしまうのではないかと思います。粘り強く文章を読解するようにして下さい。

1.正弦波交流の実効値
\( \ e=E_{\mathrm {m}}\sin \omega t \ \)で表される正弦波交流の実効値\( \ E \ \)は実効値の定義から次式で求められます。三種の場合は基本的に積分を使用しないので，結果を暗記しておく必要があります。
\[
\begin{eqnarray}
E &=& \sqrt {\frac {1}{2\pi }\int _{0}^{2\pi }\left( E_{\mathrm {m}}\sin \omega t \right) ^{2}\mathrm {d}\omega t} \\[ 5pt ] &=& \sqrt {\frac {E_{\mathrm {m}}^{2}}{2\pi }\int _{0}^{2\pi } \frac {1-\cos 2\omega t}{2} \mathrm {d}\omega t} \\[ 5pt ] &=& \sqrt {\frac {E_{\mathrm {m}}^{2}}{2\pi }\left[ \frac {1}{2}\omega t-\frac {\cos 2\omega t}{4}\right] _{0}^{2\pi }} \\[ 5pt ] &=& \sqrt {\frac {E_{\mathrm {m}}^{2}}{2\pi }\times \pi } \\[ 5pt ] &=& \sqrt {\frac {E_{\mathrm {m}}^{2}}{2}} \\[ 5pt ] &=& \frac {E_{\mathrm {m}}}{\sqrt {2}} \\[ 5pt ] \end{eqnarray}
\]

【解答】

(a)解答：(3)
題意より，基本波成分の瞬時値\( \ V_{\mathrm {A}} \ \)及び\( \ V_{\mathrm {B}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {A}}=V_{\mathrm {B}} &=& \frac {V_{\mathrm {s}}}{V_{\mathrm {c}}}\times \frac {V_{\mathrm {d}}}{2} \\[ 5pt ] &=& \frac {9}{10}\times \frac {200}{2} \\[ 5pt ] &=& 90 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] であるから，基本波成分の振幅\( \ V_{\mathrm {A-B}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {A-B}}&=&V_{\mathrm {A}}+V_{\mathrm {B}} \\[ 5pt ] &=&90+90 \\[ 5pt ] &=& 180 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。ワンポイント解説「1.正弦波交流の実効値」より，\( \ v_{\mathrm {A-B}} \ \mathrm {[V]} \ \)の基本波成分の実効値\( \ V_{\mathrm {eA-B}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {eA-B}}&=&\frac {V_{\mathrm {A-B}}}{\sqrt {2}} \\[ 5pt ] &=&\frac {180}{\sqrt {2}} \\[ 5pt ] &≒& 127 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(4)
問題図の\( \ v_{\mathrm {A-B}} = v_{\mathrm {A}}-v_{\mathrm {B}} \ \)及びその基本波成分の最初の\( \ 5 \ \mathrm {[ms]} \ \)の拡大波形より，\( \ 5 \ \mathrm {[ms]} \ \)の区間で電圧を出力している時間の合計値\( \ T_{\mathrm {s}} \ \)は，
\[
\begin{eqnarray}
T_{\mathrm {s}}&=&\left( 1.31 -0.96\right) +\left( 2.59-1.94\right) +\left( 3.80-2.93\right) +\left( 4.94-3.97\right) \\[ 5pt ] &=& 2.84 \ \mathrm {[ms]} \\[ 5pt ] \end{eqnarray}
\] であるから，実効値\( \ V_{\mathrm {rms}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {rms}} &=& \sqrt {\frac {T_{\mathrm {s}}}{5}}\times V_{\mathrm {d}} \\[ 5pt ] &=& \sqrt {\frac {2.84}{5}}\times 200 \\[ 5pt ] &≒& 151 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。