Contents
【問題】
【難易度】★★★☆☆(普通)
出力\( \ 600 \ \mathrm {[kW]} \ \)の太陽電池発電所を設置したショッピングセンターがある。ある日の太陽電池発電所の発電の状況とこのショッピングセンターにおける電力消費は図に示すとおりであった。すなわち,発電所の出力は朝の\( \ 6 \ \)時から\( \ 12 \ \)時まで直線的に増大し,その後は夕方\( \ 18 \ \)時まで直線的に下降した。また,消費電力は深夜\( \ 0 \ \)時から朝の\( \ 10 \ \)時までは\( \ 100 \ \mathrm {[kW]} \ \),\( \ 10 \ \)時から\( \ 17 \ \)時までは\( \ 300 \ \mathrm {[kW]} \ \),\( \ 17 \ \)時から\( \ 21 \ \)時までは\( \ 400 \ \mathrm {[kW]} \ \),\( \ 21 \ \)時から\( \ 24 \ \)時までは\( \ 100 \ \mathrm {[kW]} \ \)であった。
このショッピングセンターは自然エネルギーの活用を推進しており太陽電池発電所の発電電力は自家消費しているが,その発電電力が消費電力を上回って余剰を生じたときは電力系統に送電している。次の(a)及び(b)の問に答えよ。
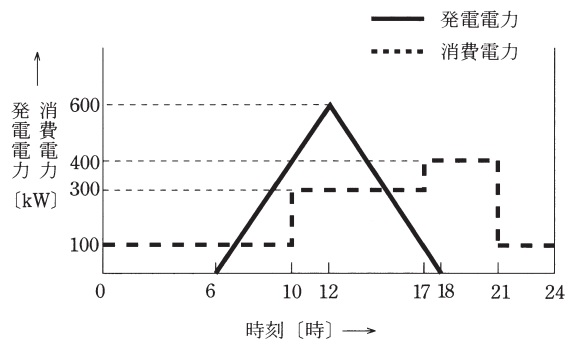
(a) この日,太陽電池発電所から電力系統に送電した電力量\( \ \mathrm {[kW\cdot h]} \ \)の値として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 900 \ \) (2) \( \ 1 \ 300 \ \) (3) \( \ 1 \ 500 \ \) (4) \( \ 2 \ 200 \ \) (5) \( \ 3 \ 600 \ \)
(b) この日,ショッピングセンターで消費した電力量に対して太陽電池発電所が発電した電力量により自給した比率\( \ \mathrm {[%]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 35 \ \) (2) \( \ 38 \ \) (3) \( \ 46 \ \) (4) \( \ 52 \ \) (5) \( \ 58 \ \)
【ワンポイント解説】
太陽電池発電所を設置したショッピングセンターの電力需給に関する問題です。
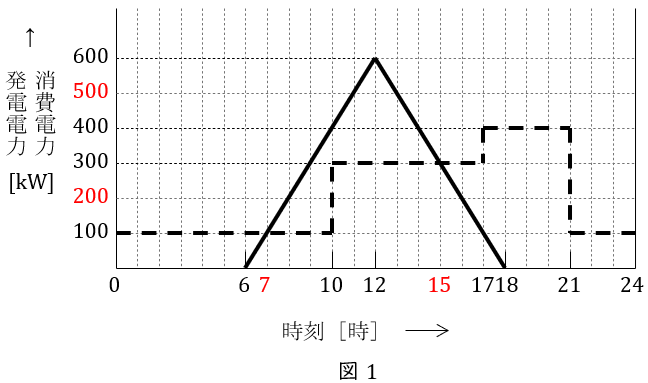
特別な公式は必要なく,論理的な考え方や正しい計算ができるかどうかが問われる問題となります。下の図1のように実際に答案に線を引き,このショッピングセンターにおいて何時から何時までが送電,何時から何時までが受電であるかを把握すると分かりやすくなると思います。
【解答】
(a)解答:(2)
図1より,太陽電池発電所から電力系統に送電した時刻は\( \ 7 \ \)時から\( \ 15 \ \)時までとなる。
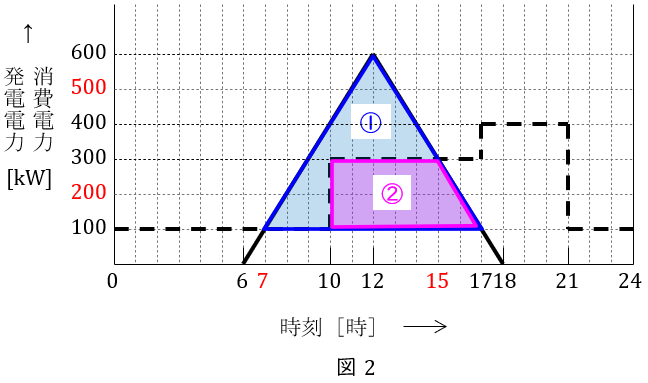
送電した電力量は発電した電力量から消費電力を差し引いた値となるので,図2の①の三角形の面積から②の台形の面積を差し引いた値となる。
したがって,送電した電力量\( \ W_{\mathrm {t}} \ \mathrm {[kW\cdot h]} \ \)は,
\[
\begin{eqnarray}
W_{\mathrm {t}} &=& (①の面積)-(②の面積) \\[ 5pt ]
&=& \frac {10\times 500}{2}-\frac {(5+7)\times 200}{2} \\[ 5pt ]
&=& 2 \ 500-1 \ 200 \\[ 5pt ]
&=& 1 \ 300 \ \mathrm {[kW\cdot h]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(b)解答:(3)
この日,太陽光発電所が発電した電力量\( \ W_{\mathrm {g}} \ \mathrm {[kW\cdot h]} \ \)は,
\[
\begin{eqnarray}
W_{\mathrm {g}} &=& \frac {12\times 600}{2} \\[ 5pt ]
&=& 3 \ 600 \ \mathrm {[kW\cdot h]} \\[ 5pt ]
\end{eqnarray}
\]
である。
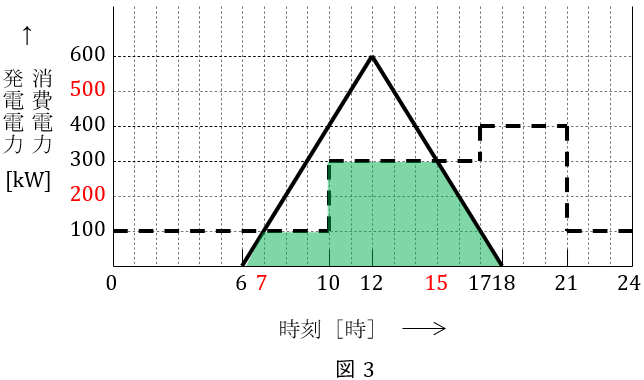
この日,ショッピングセンターが太陽光発電所の電力により自給した範囲は図3で示した範囲となる。太陽光発電所が自給した電力量\( \ W_{\mathrm {s}} \ \mathrm {[kW\cdot h]} \ \)は太陽光発電所が発電した電力量\( \ W_{\mathrm {g}} \ \mathrm {[kW\cdot h]} \ \)から,(1)の送電した電力量\( \ W_{\mathrm {t}} \ \mathrm {[kW\cdot h]} \ \)を差し引いたものであるから,
\[
\begin{eqnarray}
W_{\mathrm {s}} &=& W_{\mathrm {g}}-W_{\mathrm {t}} \\[ 5pt ]
&=& 3 \ 600-1 \ 300 \\[ 5pt ]
&=& 2 \ 300 \ \mathrm {[kW\cdot h]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
一方,この日ショッピングセンターで消費した電力量\( \ W_{\mathrm {c}} \ \mathrm {[kW\cdot h]} \ \)は,
\[
\begin{eqnarray}
W_{\mathrm {c}} &=& 10\times 100+7\times 300+4\times 400 +100\times 3 \\[ 5pt ]
&=& 5 \ 000 \ \mathrm {[kW\cdot h]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,電力の自給率\( \ \mathrm {[%]} \ \)は,
\[
\begin{eqnarray}
\frac {W_{\mathrm {s}}}{W_{\mathrm {c}}}\times 100 &=& \frac {2 \ 300}{5 \ 000}\times 100 \\[ 5pt ]
&=& 46 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは