《法規》〈電気施設管理〉[H28:問13]高圧地絡システムに関する計算問題

【問題】

【難易度】★★★☆☆（普通）

図は，線間電圧\( \ V \ \mathrm { [ V ] } \ \)，周波数\( \ f \ \mathrm { [ Hz ] } \ \)の中性点非接地方式の三相\( \ 3 \ \)線式高圧配電線路及びある需要設備の高圧地絡保護システムを簡易に示した単線図である。高圧配電線路一相の全対地静電容量を\( \ C_{1} \ \mathrm { [ F ] } \ \)，需要設備一相の全対地静電容量を\( \ C_{2} \ \mathrm { [ F ] } \ \)とするとき，次の(a)及び(b)の問に答えよ。

ただし，図示されていない負荷，線路定数及び配電用変電所の制限抵抗は無視するものとする。

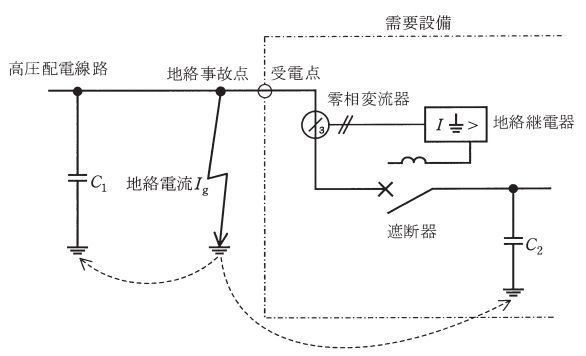
(a)　図の配電線路において，遮断器が「入」の状態で地絡事故点に一線完全地絡事故が発生し地絡電流\( \ I_{\mathrm {g}} \ \mathrm { [ A ] } \ \)が流れた。このとき\( \ I_{\mathrm {g}} \ \)の大きさを表す式として正しいものは次のうちどれか。
ただし，間欠アークによる影響等は無視するものとし，この地絡事故によって遮断器は遮断しないものとする。

　(1)　\(\displaystyle \frac {2}{\sqrt {3}}V\pi f\sqrt {\left( C_{1}^{2}+C_{2}^{2}\right) }\)　　(2)　\(\displaystyle 2\sqrt {3}V\pi f\sqrt {\left( C_{1}^{2}+C_{2}^{2}\right) }\)
　(3)　\(\displaystyle \frac {2}{\sqrt {3}}V\pi f \left( C_{1}+C_{2}\right) \)　　　(4)　\(\displaystyle 2\sqrt {3}V\pi f \left( C_{1}+C_{2}\right) \)
　(5)　\(\displaystyle 2\sqrt {3}V\pi f\sqrt {C_{1}C_{2} }\)

(b)　上記(a)の地絡電流\( \ I_{\mathrm {g}} \ \)は高圧配電線路側と需要設備側に分流し，需要設備側に分流した電流は零相変流器を通過して検出される。上記のような需要設備構外の事故に対しても，零相変流器が検出する電流の大きさによっては地絡継電器が不必要に動作する場合があるので注意しなければならない。地絡電流\( \ I_{\mathrm {g}} \ \)が高圧配電線路側と需要設備側に分流する割合は\( \ C_{1} \ \)と\( \ C_{2} \ \)の比によって決まるものとしたとき，\( \ I_{\mathrm {g}} \ \)のうち需要設備の零相変流器で検出される電流の値\( \ \mathrm { [ mA ] } \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし，\( \ V=6 \ 600 \ \mathrm { V } \ \)，\( \ f=60 \ \mathrm { Hz } \ \)，\( \ C_{1}=2.3 \ \mathrm { \mu F } \ \)，\( \ C_{2}=0.02 \ \mathrm { \mu F } \ \)とする。

　(1)　\( \ 54 \ \)　　(2)　\( \ 86 \ \)　　(3)　\( \ 124 \ \)　　(4)　\( \ 152 \ \)　　(5)　\( \ 256 \ \)

【ワンポイント解説】

法規科目ですが，中身はほとんど電力科目の問題です。題意の条件にて一線地絡が発生した時，どのように電流が流れるかを考え検討する必要があります。

1.テブナンの定理
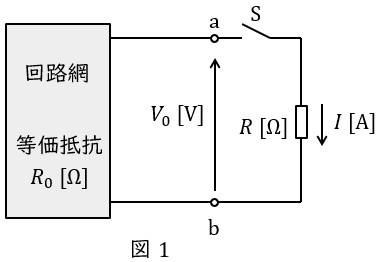
図1のような回路において，端子\( \ \mathrm {a-b} \ \)の開放電圧を\( \ V_{\mathrm {0}} \ \mathrm {[V]} \ \)，端子\( \ \mathrm {a-b} \ \)から電源側をみた合成抵抗を\( \ R_{\mathrm {0}} \ \mathrm {[\Omega ]} \ \)とする（ただし，電圧源は短絡，電流源は開放する）と，図の抵抗\( \ R \ \mathrm {[\Omega ]} \ \)を流れる電流の大きさ\( \ I \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I&=&\frac {V_{\mathrm {0}}}{R+R_{0}} \\[ 5pt ] \end{eqnarray}
\] で求められます。この関係は抵抗のみでなく，リアクタンスにも適用可能です。

2.配電線\( \ 1 \ \)線地絡時の等価回路
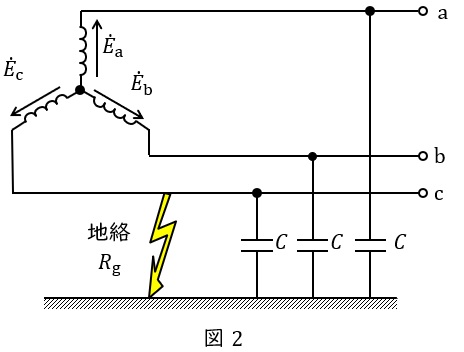
図2のような変圧器に接続された三相線路があり，\( \ \mathrm {c} \ \)相に\( \ 1 \ \)線地絡事故が発生したとします。
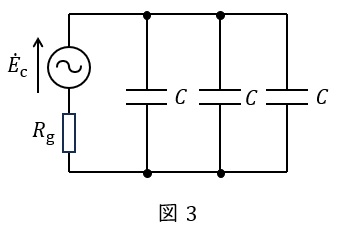
地絡点にテブナンの定理を適用すると，地絡点の開放電圧は\( \ {\dot E}_{\mathrm {c}} \ \)，地絡点から見たインピーダンスは電源を短絡して考えれば良いので，各相の静電容量が並列に接続された状態となります。したがって，等価回路は図3のように描くことができます。

【解答】

(a)解答：(4)
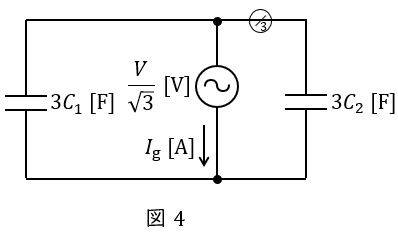
本問においては，地絡事故点にて一線完全地絡事故が発生したので，地絡抵抗\( \ R_{\mathrm {g}}=0 \ \mathrm {[\Omega ]} \ \)となり，地絡点から\( \ C_{1} \ \mathrm {[F]} \ \)と\( \ C_{2} \ \mathrm {[F]} \ \)に分流するため，等価回路は図4のようになる。
図4より，地絡電流\( \ I_{\mathrm {g}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {g}}&=&2\pi f\times 3C_{1} \frac {V}{\sqrt {3}}+2\pi f\times 3C_{2} \frac {V}{\sqrt {3}} \\[ 5pt ] &=&6\pi f\frac {V}{\sqrt {3}}\left( C_{1}+ C_{2}\right) \\[ 5pt ] &=&2\sqrt {3}V \pi f\left( C_{1}+ C_{2}\right) \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(2)
零相変流器で検出される電流の値は図4における\( \ 3C_{2} \ \)を流れる電流\( \ I_{\mathrm {C2}} \ \mathrm {[A]} \ \)であるから，
\[
\begin{eqnarray}
I_{\mathrm {C2}}&=&2\pi f \times 3C_{2} \frac {V}{\sqrt {3}} \\[ 5pt ] &=&2\sqrt {3}V \pi fC_{2} \\[ 5pt ] \end{eqnarray}
\] となり，各値を代入すると，
\[
\begin{eqnarray}
I_{\mathrm {C2}}&=&2\sqrt {3}\times 6 \ 600\times \pi\times 60 \times 0.02\times 10^{-6} \\[ 5pt ] &≒&0.0862 \ \mathrm {[A]}　→　86 \ \mathrm {[mA]} \\[ 5pt ] \end{eqnarray}
\] と求められる。