Contents
【問題】
【難易度】★★★★☆(やや難しい)
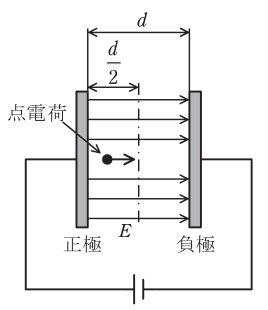
図のように,極板間の距離\( \ d \ \mathrm {[m]} \ \)の平行板導体が真空中に置かれ,極板間に強さ\( \ E \ \mathrm {[V/m]} \ \)の一様な電界が生じている。質量\( \ m \ \mathrm {[kg]} \ \),電荷量\( \ q ( >0 ) \ \mathrm {[C]} \ \)の点電荷が正極から放出されてから,極板間の中心\( \ \displaystyle \frac {d}{2} \ \mathrm {[m]} \ \)に達するまでの時間\( \ t \ \mathrm {[s]} \ \)を表す式として,正しいものを次の(1)~(5)のうちから一つ選べ。
ただし,点電荷の速度は光速より十分小さく,初速度は\( \ 0 \ \mathrm {m/s} \ \)とする。また,重力の影響は無視できるものとし,平行板導体は十分大きいものとする。
(1) \(\displaystyle \sqrt {\frac {md}{qE}}\) (2) \(\displaystyle \sqrt {\frac {2md}{qE}}\) (3) \(\displaystyle \sqrt {\frac {qEd}{m}}\) (4) \(\displaystyle \sqrt {\frac {qE}{md}}\) (5) \(\displaystyle \sqrt {\frac {2qE}{md}}\)
【ワンポイント解説】
平行平板コンデンサ中の電荷に働く力と高校の力学の問題を組み合わせたような問題となっています。いくつかの公式を理解している必要があります。決して公式を丸暗記するのではなく,理解するようにしておきましょう。
1.電荷に働く力の大きさ
一様な電界\( \ E \ \)が電荷\( \ q \ \)にかかっているとき,この電荷\( \ q \ \)に働く力の大きさ\( \ F \ \)は,
\[
\begin{eqnarray}
F &=&qE \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.運動方程式
質量\( \ m \ \)の物体に力\( \ F \ \)がかかっている時,この物体にかかる加速度\( \ a \ \)との間には,
\[
\begin{eqnarray}
F &=&ma \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。
3.物体の運動に関する公式
基準となる位置\( \ x_{0} \ \mathrm {[m]} \ \)にある物体が,初速度\( \ v_{0} \ \mathrm {[m/s]} \ \),加速度\( \ a \ \mathrm {[m/s^{2}]} \ \)で運動しているとすると,時刻\( \ t \ \mathrm {[s]} \ \)後の位置\( \ x \ \mathrm {[m]} \ \)は,
\[
\begin{eqnarray}
x &=&x_{0}+v_{0}t+\frac {1}{2}at^{2} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
解答:(1)
ワンポイント解説「1.電荷に働く力の大きさ」及び「2.運動方程式」の通り,点電荷の運動方程式から加速度を求めると,
\[
\begin{eqnarray}
F &=&ma \\[ 5pt ]
qE &=&ma \\[ 5pt ]
a &=&\frac {qE}{m} \\[ 5pt ]
\end{eqnarray}
\]
となる。ワンポイント解説「3.物体の運動に関する公式」より,\( \ \displaystyle \frac {d}{2} \ \mathrm {[m]} \ \)に到達するまでの時間\( \ t \ \mathrm {[s]} \ \)は,初期位置\( \ 0 \ \mathrm {[m]} \ \),初速度\( \ 0 \ \mathrm {[m/s]} \ \)であるから,
\[
\begin{eqnarray}
\frac {d}{2} &=&\frac {1}{2}at^{2} \\[ 5pt ]
\frac {d}{2}&=&\frac {1}{2}\frac {qE}{m}t^{2} \\[ 5pt ]
d&=&\frac {qE}{m}t^{2} \\[ 5pt ]
t^{2}&=&\frac {md}{qE} \\[ 5pt ]
t&=&\sqrt {\frac {md}{qE}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは