Contents
【問題】
【難易度】★★★★☆(やや難しい)
三相\( \ 3 \ \)線式配電線路の受電端に遅れ力率\( \ 0.8 \ \)の三相平衡負荷\( \ 60 \ \mathrm {[kW]} \ \)(一定)が接続されている。次の(a)及び(b)の問に答えよ。
ただし,三相負荷の受電端電圧は\( \ 6.6 \ \mathrm {kV} \ \)一定とし,配電線路のこう長は\( \ 2.5 \ \mathrm {[km]} \ \),電線\( \ 1 \ \)線当たりの抵抗は\( \ 0.5 \ \mathrm {\Omega /km} \ \), リアクタンスは\( \ 0.2 \ \mathrm {\Omega /km} \ \)とする。なお,送電端電圧と受電端電圧の位相角は十分小さいものとして得られる近似式を用いて解答すること。また,配電線路こう長が短いことから,静電容量は無視できるものとする。
(a) この配電線路での抵抗による電力損失の値\( \ \mathrm {[W]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \(22\) (2) \(54\) (3) \(65\) (4) \(161\) (5) \(220\)
(b) 受電端の電圧降下率を\( \ 2.0 \ \mathrm {%} \ \)以内にする場合,受電端でさらに増設できる負荷電力(最大)の値\( \ \mathrm {[kW]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。ただし,負荷の力率(遅れ)は変わらないものとする。
(1) \(476\) (2) \(536\) (3) \(546\) (4) \(1280\) (5) \(1340\)
【ワンポイント解説】
電験\( \ 3 \ \)種の配電線の負荷電力の計算に関する問題です。少し骨のある問題ですが,電圧降下に関する計算は重要な内容となりますので,じっくりと解くようにして下さい。
1.配電線の電圧降下の近似式
①単相回路の電圧降下
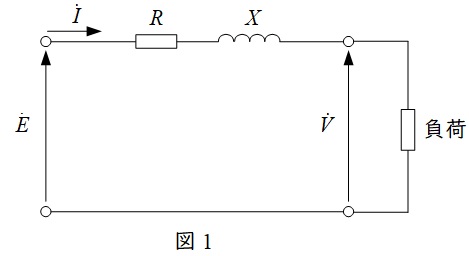
図1のような回路において,ベクトル図を描くと図2のようになります。
図2のベクトル図において,\(\dot E \)と\(\dot V\)の位相差が十分に小さいと仮定すると,線路の電圧降下\( \ \varepsilon =E-V \ \)は,
\[
\begin{eqnarray}
E&≃&V+RI\cos \theta +XI\sin \theta \\[ 5pt ]
E-V&=&RI\cos \theta +XI\sin \theta \\[ 5pt ]
\varepsilon &=&I\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ]
\end{eqnarray}
\]
と求められます。

②三相\( \ 3 \ \)線式送電線の電圧降下
三相回路においても,一相分の等価回路及びベクトル図は図1及び図2のように描くことができ,三相分の電圧降下\( \ \varepsilon \ \)は,
\[
\begin{eqnarray}
\varepsilon &=&\sqrt {3}I\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ]
\end{eqnarray}
\]
と求められます。
※従って本問においては\( \ \sqrt {3} \ \)の計算忘れに注意が必要です。
また,電圧降下率\( \ e \ \)は,受電端電圧を\( \ V_{\mathrm {r}} \ \)とすると,
\[
\begin{eqnarray}
e &=&\frac {\varepsilon }{V_{\mathrm {r}}}\times 100 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.三相線路の電力\( \ P \ \)と電圧\( \ V \ \),電流\( \ I \ \)の関係
電圧と電流の位相差を\( \ \theta \ \),力率を\( \ \cos \theta \ \)とすると,
\[
\begin{eqnarray}
P&=&\sqrt {3}VI\cos \theta \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(a)解答:(4)
題意より,配電線の抵抗\( \ R \ \)及びリアクタンス\( \ X \ \)の大きさは,
\[
\begin{eqnarray}
R &=&0.5\times 2.5 \\[ 5pt ]
&=&1.25 \ \mathrm {[\Omega ]} \\[ 5pt ]
X &=&0.2\times 2.5 \\[ 5pt ]
&=&0.5 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
である。ワンポイント解説「2.三相線路の電力\( \ P \ \)と電圧\( \ V \ \),電流\( \ I \ \)の関係」より,\( \ P=\sqrt {3}V_{\mathrm {r}}I\cos \theta \ \)であるから,配電線を流れる電流\( \ I \ \)は
\[
\begin{eqnarray}
I &=&\frac {P}{\sqrt {3}V_{\mathrm {r}}\cos \theta } \\[ 5pt ]
&=&\frac {60\times 10^{3}}{\sqrt {3}\times 6.6\times 10^{3}\times 0.8 } \\[ 5pt ]
&≒&6.561 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
であるので,配電線路での抵抗による電力損失\( \ P_{\mathrm {r}} \ \mathrm {[W]} \ \)は,一相あたりの電力損失が\( \ RI^{2} \ \)であるから,
\[
\begin{eqnarray}
P_{\mathrm {r}} &=&3RI^{2} \\[ 5pt ]
&=&3\times 1.25\times 6.561^{2} \\[ 5pt ]
&≒&161 \ \mathrm {[W]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(b)解答:(1)
ワンポイント解説「1.配電線の電圧降下の近似式」より,電圧降下率\( \ 2.0 \ \mathrm {%} \ \)の時の電圧降下\( \ \varepsilon \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
\varepsilon &=&6.6\times 10^{3}\times \frac {2.0}{100} \\[ 5pt ]
&=&132 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
である。また,\( \ \sin ^{2}\theta +\cos ^{2}\theta =1 \ \)より,
\[
\begin{eqnarray}
\sin \theta &=&\sqrt {1-\cos ^{2}\theta } \\[ 5pt ]
&=&\sqrt {1-0.8 ^{2}} \\[ 5pt ]
&=&0.6 \\[ 5pt ]
\end{eqnarray}
\]
なる。電圧降下の近似式より配電線路に流すことが可能な最大電流\( \ I_{\mathrm {m}} \ \)は,
\[
\begin{eqnarray}
\varepsilon &=&\sqrt {3}I_{\mathrm {m}}\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ]
I_{\mathrm {m}}&=&\frac {\varepsilon }{\sqrt {3}\left( R\cos \theta +X\sin \theta \right) } \\[ 5pt ]
&=&\frac {132}{\sqrt {3}\left( 1.25 \times 0.8 +0.5\times 0.6 \right) } \\[ 5pt ]
&≒&58.62 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,受電端に接続することができる最大電力\( \ P_{\mathrm {m}} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {m}} &=&\sqrt {3}V_{\mathrm {r}}I_{\mathrm {m}}\cos \theta \\[ 5pt ]
&=&\sqrt {3}\times 6.6\times 10^{3}\times 58.62\times 0.8 \\[ 5pt ]
&≒&536093 \ \mathrm {[W]} → 536 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,増設できる負荷電力は\( \ 476 \ \mathrm {[kW]} \ \)と求められる。





















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは