Contents
【問題】
【難易度】★★★☆☆(普通)
直流電源に接続された永久磁石界磁の直流電動機に一定トルクの負荷がつながっている。電機子抵抗が\( \ 1.00 \ \Omega \ \)である。回転速度が\( \ 1000 \ \mathrm {min}^{-1} \ \)のとき,電源電圧は\( \ 120 \ \mathrm {V} \ \),電流は\( \ 20 \ \mathrm {A} \ \)であった。
この電源電圧を\( \ 100 \ \mathrm {V} \ \)に変化させたときの回転速度の値\( \ \mathrm {[{min}^{-1}]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし,電機子反作用及びブラシ,整流子における電圧降下は無視できるものとする。
(1) \(200\) (2) \(400\) (3) \(600\) (4) \(800\) (5) \(1000\)
【ワンポイント解説】
直流電動機の問題はほぼ毎年出題されています。基本は等価回路を描き,それぞれの特性がどのようになるかを理解すれば解けると思います。
1.直流機の誘導起電力(逆起電力)\( \ E \ \)
磁極の数\( \ p \ \),電機子導体数\( \ Z \ \),電機子巻線並列回路数\( \ a \ \),各極の磁束\( \ \phi \ \),回転速度\( \ N \ \)とすると,直流機の誘導起電力(逆起電力)\( \ E \ \)は,
\[
\begin{eqnarray}
E &=&\frac {pZ}{60a}\phi N \\[ 5pt ]
&=&k_{\mathrm {e}}\phi N \\[ 5pt ]
\end{eqnarray}
\]
となり,磁束\( \ \phi \ \)と回転速度\( \ N \ \)に比例します。
2.直流機のトルク\( \ T \ \)
磁極の数\( \ p \ \),電機子導体数\( \ Z \ \),電機子巻線並列回路数\( \ a \ \),各極の磁束\( \ \phi \ \),電機子電流\( \ I_{\mathrm {a}} \ \)とすると,直流機のトルク\( \ T \ \)は,
\[
\begin{eqnarray}
T &=&\frac {pZ}{2\pi a}\phi I_{\mathrm {a}} \\[ 5pt ]
&=&k_{\mathrm {f}}\phi I_{\mathrm {a}} \\[ 5pt ]
\end{eqnarray}
\]
となり,磁束\( \ \phi \ \)と電機子電流\( \ I_{\mathrm {a}} \ \)に比例します。
【解答】
解答:(4)
題意の直流機の等価回路を図1に示す。図において,\( \ E \ \)は逆起電力,\( \ V \ \)は電源電圧,\( \ I_{\mathrm {a}} \ \)は電機子電流,\( \ R_{\mathrm {a}} \ \)は電機子巻線の抵抗値とする。
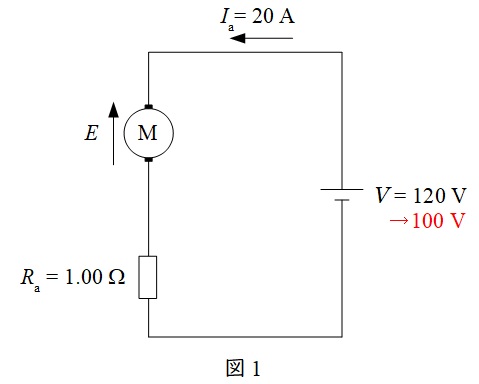
図1より,逆起電力\( \ E \ \)の大きさは,
\[
\begin{eqnarray}
E &=&V-R_{\mathrm {a}}I_{\mathrm {a}} \\[ 5pt ]
&=&120-1.00\times 20 \\[ 5pt ]
&=&100 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となり,この時回転速度が\( \ 1000 \ \mathrm {min}^{-1} \ \)である。
次に,電源電圧\( \ V^{\prime } =100 \ \mathrm {V} \ \)に変化させたときを検討する。ワンポイント解説「2.直流機のトルク\( \ T \ \)」より,
\[
\begin{eqnarray}
T &=&k_{\mathrm {f}}\phi I_{\mathrm {a}} \\[ 5pt ]
I_{\mathrm {a}} &=&\frac {T}{k_{\mathrm {f}}\phi } \\[ 5pt ]
\end{eqnarray}
\]
である。永久磁石界磁であるため,\( \ \phi \ \)は変化せず,外部負荷は一定トルクであるため,電機子電流\( \ I_{\mathrm {a}} \ \)も一定となる。したがって,この時の逆起電力\( \ E^{\prime } \ \)は,
\[
\begin{eqnarray}
E^{\prime } &=&V^{\prime }-R_{\mathrm {a}}I_{\mathrm {a}} \\[ 5pt ]
&=&100-1.00\times 20 \\[ 5pt ]
&=&80 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となる。ワンポイント解説「1.直流機の誘導起電力(逆起電力)\( \ E \ \)」より,
\[
\begin{eqnarray}
E &=&\frac {pZ}{60a}\phi N \\[ 5pt ]
&=&k_{\mathrm {e}}\phi N \\[ 5pt ]
\end{eqnarray}
\]
であり,永久磁石界磁であるため,\( \ \phi \ \)は変化しないので,逆起電力\( \ E \ \)と回転速度\( \ N \ \)は比例する。したがって,電圧変更前後の回転速度を\( \ N \ \)及び\( \ N^{\prime } \ \)とすると,
\[
\begin{eqnarray}
\frac {E^{\prime }}{E} &=&\frac {N^{\prime }}{N} \\[ 5pt ]
\frac {80}{100} &=&\frac {N^{\prime }}{1000} \\[ 5pt ]
N^{\prime }&=&800 \ \mathrm {[{min}^{-1}]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは