Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,直流他励電動機の制御に関する記述である。ただし,鉄心の磁気飽和と電機子反作用は無視でき,また,電機子抵抗による電圧降下は小さいものとする。
a 他励電動機は,\( \ \fbox { (ア) } \ \)と\( \ \fbox { (イ) } \ \)を独立した電源で制御できる。磁束は\( \ \fbox { (ア) } \ \)に比例する。
b 磁束一定の条件で\( \ \fbox { (イ) } \ \)を増減すれば,\( \ \fbox { (イ) } \ \)に比例するトルクを制御できる。
c 磁束一定の条件で\( \ \fbox { (ウ) } \ \)を増減すれば,\( \ \fbox { (ウ) } \ \)に比例する回転数を制御できる。
d \( \ \fbox { (ウ) } \ \)一定の条件で磁束を増減すれば,ほぼ磁束に反比例する回転数を制御できる。回転数の\( \ \fbox { (エ) } \ \)のために\( \ \fbox { (ア) } \ \)を弱める制御がある。
このように広い速度範囲で速度とトルクを制御できるので,直流他励電動機は圧延機の駆動などに広く使われてきた。
上記の記述中の空白箇所(ア)~(エ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{ccccc}
& (ア) & (イ) & (ウ) & (エ) \\
\hline
(1) & 界磁電流 & 電機子電流 & 電機子電圧 & 上昇 \\
\hline
(2) & 電機子電流 & 界磁電流 & 電機子電圧 & 上昇 \\
\hline
(3) & 電機子電圧 & 電機子電流 & 界磁電流 & 低下 \\
\hline
(4) & 界磁電流 & 電機子電圧 & 電機子電流 & 低下 \\
\hline
(5) & 電機子電圧 & 電機子電流 & 界磁電流 & 上昇 \\
\hline
\end{array}
\]
【ワンポイント解説】
ほぼ毎年出題される直流電動機の分野からの出題です。
このような空欄穴埋問題においても,等価回路を描き,関係式から正答を導くという基本は計算問題と同じなので,等価回路は確実にマスターしておきましょう。
1.直流他励電動機の等価回路
図1に直流他励電動機の等価回路を示します。図1において,\( \ V \ \)は端子電圧,\( \ E \ \)は逆起電力,\( \ V_{\mathrm {f}} \ \)は界磁電圧,\( \ I_{\mathrm {a}} \ \)は電機子電流,\( \ I_{\mathrm {f}} \ \)は界磁電流,\( \ R_{\mathrm {a}} \ \)は電機子抵抗,\( \ R_{\mathrm {f}} \ \)は界磁抵抗となります。
他励式の特徴としては,界磁回路が独立しているので,界磁磁束を独立して制御できるという特徴があります。
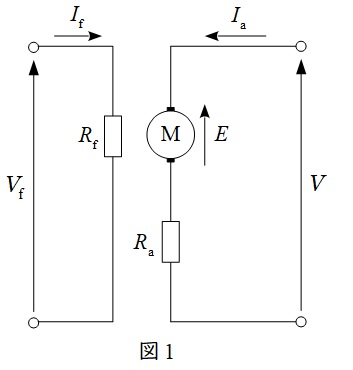
また,上記の等価回路にキルヒホッフの法則を適用すると,以下の関係式が導き出せることが分かります。
\[
\begin{eqnarray}
V &=& E+R_{\mathrm {a}}I_{\mathrm {a}} \\[ 5pt ]
I_{\mathrm {f}} &=& \frac {V_{\mathrm {f}}}{R_{\mathrm {f}}} \\[ 5pt ]
\end{eqnarray}
\]
2.直流機の誘導起電力(逆起電力)\( \ E \ \)
磁極の数\( \ p \ \),電機子導体数\( \ Z \ \),電機子巻線並列回路数\( \ a \ \),各極の磁束\( \ \phi \ \),回転速度\( \ N \ \)とすると,直流機の誘導起電力(逆起電力)\( \ E \ \)は,
\[
\begin{eqnarray}
E &=&\frac {pZ}{60a}\phi N \\[ 5pt ]
&=&k_{\mathrm {e}}\phi N \\[ 5pt ]
\end{eqnarray}
\]
となり,磁束\( \ \phi \ \)と回転速度\( \ N \ \)に比例します。
3.直流機のトルク\( \ T \ \)
磁極の数\( \ p \ \),電機子導体数\( \ Z \ \),電機子巻線並列回路数\( \ a \ \),各極の磁束\( \ \phi \ \),電機子電流\( \ I_{\mathrm {a}} \ \)とすると,直流機のトルク\( \ T \ \)は,
\[
\begin{eqnarray}
T &=&\frac {pZ}{2\pi a}\phi I_{\mathrm {a}} \\[ 5pt ]
&=&k_{\mathrm {f}}\phi I_{\mathrm {a}} \\[ 5pt ]
\end{eqnarray}
\]
となり,磁束\( \ \phi \ \)と電機子電流\( \ I_{\mathrm {a}} \ \)に比例します。
【解答】
解答:(1)
(ア)
ワンポイント解説「1.直流他励電動機の等価回路」の通り,他励電動機は界磁回路と電機子回路が独立しており,磁束は図1の通り電機子電流\( \ I_{\mathrm {a}} \ \)や電機子電圧には関係せず,界磁電流\( \ I_{\mathrm {f}} \ \)に比例します。
(イ)
ワンポイント解説「3.直流機のトルク\( \ T \ \)」の通り,直流機のトルク\( \ T \ \)は,
\[
\begin{eqnarray}
T &=&k_{\mathrm {f}}\phi I_{\mathrm {a}} \\[ 5pt ]
\end{eqnarray}
\]
となり,磁束\( \ \phi \ \)が一定の条件では電機子電流\( \ I_{\mathrm {a}} \ \)に比例します。
(ウ)
ワンポイント解説「2.直流機の誘導起電力(逆起電力)\( \ E \ \)」の通り,直流機の逆起電力\( \ E \ \)と回転数\( \ N \ \)には,
\[
\begin{eqnarray}
E &=&k_{\mathrm {e}}\phi N \\[ 5pt ]
N&=&\frac {E}{k_{\mathrm {e}}\phi } \\[ 5pt ]
\end{eqnarray}
\]
の関係があるので,磁束一定の条件では電機子電圧に比例することが分かります。
※ここでいう電機子電圧が端子電圧\( \ V \ \)なのか逆起電力\( \ E \ \)なのかが疑問ですが,一般的には電機子電圧というと\( \ V \ \)のイメージである気がします。\( \ V \ \)である場合,ワンポイント解説「1.直流他励電動機の等価回路」より,
\[
\begin{eqnarray}
V &=& E+R_{\mathrm {a}}I_{\mathrm {a}} \\[ 5pt ]
E &=& V-R_{\mathrm {a}}I_{\mathrm {a}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
N&=&\frac {V-R_{\mathrm {a}}I_{\mathrm {a}}}{k_{\mathrm {e}}\phi } \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ R_{\mathrm {a}}I_{\mathrm {a}} \ \ \)が十分に小さいならば,
\[
\begin{eqnarray}
N&≃&\frac {V}{k_{\mathrm {e}}\phi } \\[ 5pt ]
\end{eqnarray}
\]
となり,ほぼ比例の関係になることがわかります。
(エ)
(ア)及び(ウ)より,界磁電流\( \ I_{\mathrm {f}} \ \)を弱めると界磁磁束\( \ \phi \ \)が小さくなり,回転数が\( \ N \ \)が上昇します。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは