《電力》〈配電〉[H24:問11]地中配電ケーブルの充電容量に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

電圧\( \ 6.6 \ \mathrm {[kV]} \ \)，周波数\( \ 50 \ \mathrm {[Hz]} \ \)，こう長\( \ 1.5 \ \mathrm {[km]} \ \)の交流三相\( \ 3 \ \)線式地中電線路がある。ケーブルの心線\( \ 1 \ \)線当たりの静電容量を\( \ 0.35 \ \mathrm {[\mu F ／km]} \ \)とするとき，このケーブルの心線\( \ 3 \ \)線を充電するために必要な容量\( \ \mathrm {[kV\cdot A]} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\(4.2\)　　(2)　\(4.8\)　　(3)　\(7.2\)　　(4)　\(12\)　　(5)　\(37\)　

【ワンポイント解説】

ケーブルの充電電流に関する問題で，非常に出題されやすい内容となります。一相分等価回路を描くことができれば中間ポイントまでたどり着いたと考えて良いと思います。

1.ケーブル線路の充電容量
ケーブルは通常の絶縁電線と比較して静電容量が非常に大きいため，対地静電容量による充電電流を十分考慮する必要があります。通常対地静電容量を考える場合，ケーブルの中間点から大地の間のコンデンサ\( \ C \ \mathrm {[F]} \ \)として考え，無負荷の三相\( \ 3 \ \)線式地中電線路の等価回路は図1のようになります。

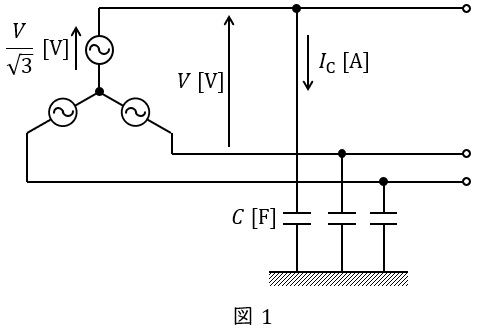
図1において，電源の中性点は三相平衡時\( \ 0 \ \mathrm {[V]} \ \)であり，三相が対称回路であるため，一相分等価回路を描くと図2のようになります。

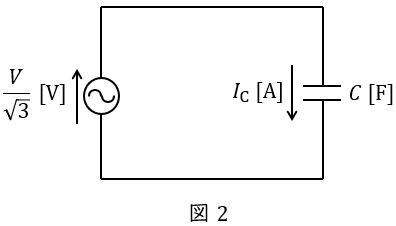
このとき，電源の線間電圧が\( \ V \ \mathrm {[V]} \ \)，周波数が\( \ f \ \mathrm {[Hz]} \ \)であるとすると，ケーブル一相分の充電電流\( \ I_{\mathrm {C}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {C}}&=&\frac {\displaystyle \frac {V}{\sqrt {3}}}{\displaystyle \frac {1}{\omega C}} \\[ 5pt ] &=&\frac {\omega CV}{\sqrt {3}} \\[ 5pt ] &=&\frac {2\pi fCV}{\sqrt {3}} \\[ 5pt ] \end{eqnarray}
\] となり，三相分の充電容量\( \ Q_{\mathrm {C}} \ \mathrm {[var]} \ \)は，
\[
\begin{eqnarray}
Q_{\mathrm {C}}&=&3\cdot \frac {V}{\sqrt {3}}I_{\mathrm {C}} \\[ 5pt ] &=&3\cdot \frac {V}{\sqrt {3}}\cdot \frac {2\pi fCV}{\sqrt {3}} \\[ 5pt ] &=&2\pi fCV^{2} \\[ 5pt ] \end{eqnarray}
\] で求められます。

【解答】

解答：(3)
題意より，ケーブル\( \ 1 \ \)線当たりの静電容量\( \ C \ \mathrm {[\mu F]} \ \)は，
\[
\begin{eqnarray}
C&=&0.35\times 1.5 \\[ 5pt ] &=&0.525 \ \mathrm {[\mu F]} \\[ 5pt ] \end{eqnarray}
\] なので，ケーブルの心線\( \ 3 \ \)線を充電するために必要な三相無負荷充電容量\( \ Q_{\mathrm {C}} \ \mathrm {[kV\cdot A]} \ \)は，ワンポイント解説「1.ケーブル線路の充電容量」の通り，
\[
\begin{eqnarray}
Q_{\mathrm {C}}&=&2\pi fCV^{2} \\[ 5pt ] &=&2\pi \times 50 \times 0.525\times 10^{-6}\times \left( 6.6\times 10^{3}\right) ^{2} \\[ 5pt ] &≒&7 \ 180 \ \mathrm {[V\cdot A]}　→　7.2 \ \mathrm {[kV\cdot A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。