《電力》〈送電〉[H24:問13]送電線のたるみの温度による変化に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

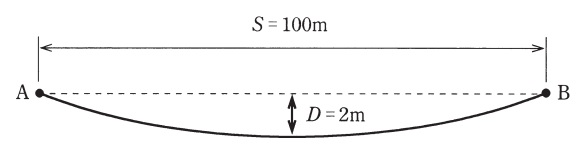
図のように高低差のない支持点\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)で支持されている径間\( \ S \ \)が\( \ 100 \ \mathrm {[m]} \ \)の架空電線路において，導体の温度が\( \ 30 \ \mathrm {[℃]} \ \)のとき，たるみ\( \ D \ \)は\( \ 2 \ \mathrm {[m]} \ \)であった。

導体の温度が\( \ 60 \ \mathrm {[℃]} \ \)になったとき，たるみ\( \ D \ \mathrm {[m]} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし，電線の線膨張係数は\( \ 1 \ \mathrm {[℃]} \ \)につき\( \ 1.5\times 10^{-5} \ \)とし，張力による電線の伸びは無視するものとする。

　(1)　\(2.05\)　　(2)　\(2.14\)　　(3)　\(2.39\)　　(4)　\(2.66\)　　(5)　\(2.89\)　

【ワンポイント解説】

電験では線膨張係数と長さの関係式は与えられることが多いですが，本問では全く与えられていません。電線の長さとたるみの関係式もあまり出題される内容ではないため，本問はかなりの受験生が苦戦したものと思います。

1.電線の長さ\( \ L \ \)とたるみ\( \ D \ \)の関係
送電線の支持点間の距離\( \ S \ \)とたるみ\( \ D \ \)が与えられている時，電線の長さ\( \ L \ \)は，
\[
\begin{eqnarray}
L&=&S+\frac {8D^{2}}{3S} \\[ 5pt ] \end{eqnarray}
\] で求められます。

2.電線の長さと温度変化の関係
電線の温度が\( \ t_{1} \ \mathrm {[℃]} \ \)の時，長さが\( \ L_{1} \ \mathrm {[m]} \ \)であった場合，\( \ t_{2} \ \mathrm {[℃]} \ \)の時の長さ\( \ L_{2} \ \mathrm {[m]} \ \)は，線膨張係数を\( \ \alpha \ \)とすると，
\[
\begin{eqnarray}
L_{2}&=&L_{1}\left \{ 1+\alpha \left( t_{2}-t_{1}\right) \right\} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(3)
ワンポイント解説「1.電線の長さ\( \ L \ \)とたるみ\( \ D \ \)の関係」より，導体の温度が\( \ 30 \ \mathrm {[℃]} \ \)のときの電線の長さ\( \ L_{1} \ \mathrm {[m]} \ \)は，
\[
\begin{eqnarray}
L_{1}&=&S+\frac {8D^{2}}{3S} \\[ 5pt ] &=&100+\frac {8\times 2^{2}}{3\times 100} \\[ 5pt ] &≒&100.1067 \ \mathrm {[m]} \\[ 5pt ] \end{eqnarray}
\] であるから，\( \ 60 \ \mathrm {[℃]} \ \)のときの電線の長さ\( \ L_{2} \ \mathrm {[m]} \ \)は，ワンポイント解説「2.電線の長さと温度変化の関係」より，
\[
\begin{eqnarray}
L_{2}&=&L_{1}\left \{ 1+\alpha \left( t_{2}-t_{1}\right) \right\} \\[ 5pt ] &=&100.1067 \times \left \{ 1+1.5\times 10^{-5}\times \left( 60-30\right) \right\} \\[ 5pt ] &≒&100.1517 \ \mathrm {[m]} \\[ 5pt ] \end{eqnarray}
\] となるので，\( \ 60 \ \mathrm {[℃]} \ \)のときのたるみ\( \ D^{\prime } \ \mathrm {[m]} \ \)は，
\[
\begin{eqnarray}
L_{2}&=&S+\frac {8{D^{\prime }}^{2}}{3S} \\[ 5pt ] \frac {8{D^{\prime }}^{2}}{3S}&=&L_{2}-S \\[ 5pt ] {D^{\prime }}^{2}&=&\frac {3S}{8}\left( L_{2}-S\right) \\[ 5pt ] D^{\prime }&=&\sqrt {\frac {3S}{8}\left( L_{2}-S\right) } \\[ 5pt ] &=&\sqrt {\frac {3\times 100}{8}\times \left( 100.1517-100\right) } \\[ 5pt ] &≒&2.39 \ \mathrm {[m]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

※　本問では\( \ 100 \ \)を引く計算があるため，有効数字は多めにとっておく必要があります。