《機械》〈パワーエレクトロニクス〉[H24:問10]サイリスタによる全波整流回路に関する論説問題

【問題】

【難易度】★★★★☆（やや難しい）

交流電圧\( \ v_{\mathrm {a}} \ \mathrm {[V]} \ \)の実効値\( \ V_{\mathrm {a}} \ \mathrm {[V]} \ \)が\( \ 100 \ \mathrm {[V]} \ \)で，抵抗負荷が接続された図1に示す半導体電力変換装置において，図2に示すようにラジアンで表した制御遅れ角\( \ \alpha \ \mathrm {[rad]} \ \)を変えて出力直流電圧\( \ v_{\mathrm {d}} \ \mathrm {[V]} \ \)の平均値\( \ V_{\mathrm {d}} \ \mathrm {[V]} \ \)を制御する。

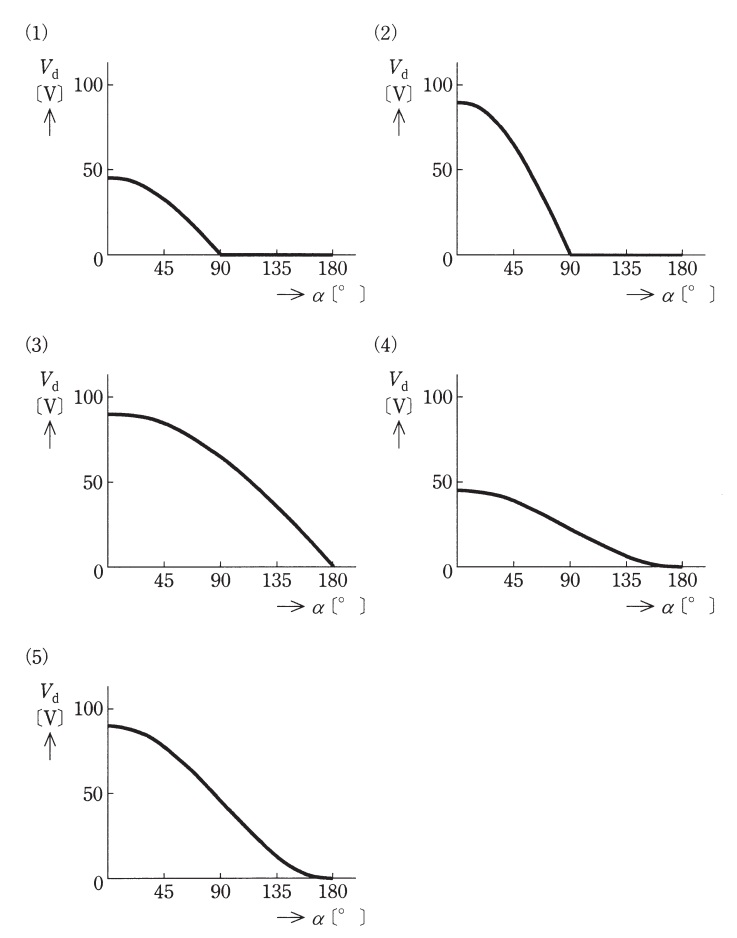
度数で表した制御遅れ角\( \ \alpha \ \mathrm {[°]} \ \)に対する\( \ V_{\mathrm {d}} \ \mathrm {[V]} \ \)の関係として，適切なものを次の(1)～(5)のうちから一つ選べ。

ただし，サイリスタの電圧降下は，無視する。

【ワンポイント解説】

パワーエレクトロニクスの問題ですが，問題で出力の波形が与えられているため，ほぼ数学の問題と言えると思います。積分計算が扱える方は，是非平均電圧の導出をやってみて下さい。積分計算をできない方は平均電圧の式を覚えることになります。

1.サイリスタによる全波整流回路の平均電圧
制御遅れ角\( \ \alpha \ \mathrm {[rad]} \ \)で制御している全波整流回路の平均電圧\( \ V_{\mathrm {d}} \ \mathrm {[V]} \ \)は，図2における\( \ \alpha \ \mathrm {[rad]} \ \)から\( \ \pi \ \mathrm {[rad]} \ \)までの電圧の合計値を\( \ \pi \ \)で割ったものであるから，
\[
\begin{eqnarray}
V_{\mathrm {d}} &=& \frac {1}{\pi }\int _{\alpha }^{\pi }\sqrt {2}V_{\mathrm {a}}\sin \omega t \mathrm {d}\omega t \\[ 5pt ] &=& \frac {\sqrt {2}}{\pi }V_{\mathrm {a}}\left[ -\cos \omega t\right] _{\alpha }^{\pi } \\[ 5pt ] &=& \frac {\sqrt {2}}{\pi }V_{\mathrm {a}}\left( 1+\cos \alpha \right) \\[ 5pt ] &≃& 0.45V_{\mathrm {a}}\left( 1+\cos \alpha \right) \\[ 5pt ] \end{eqnarray}
\] または，
\[
\begin{eqnarray}
V_{\mathrm {d}} &≃& 0.9V_{\mathrm {a}}\frac {1+\cos \alpha }{2} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(5)
\( \ \alpha =0° \ \)の時，
\[
\begin{eqnarray}
V_{\mathrm {d}} \left( 0° \right) &≃& 0.9V_{\mathrm {a}}\frac {1+\cos \alpha }{2} \\[ 5pt ] &=& 0.9\times 100\times \frac {1+\cos 0° }{2} \\[ 5pt ] &=& 0.9\times 100\times \frac {1+1 }{2} \\[ 5pt ] &=& 90 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] であり，\( \ \alpha =90° \ \)の時，
\[
\begin{eqnarray}
V_{\mathrm {d}} \left( 90° \right) &≃& 0.9V_{\mathrm {a}}\frac {1+\cos \alpha }{2} \\[ 5pt ] &=& 0.9\times 100\times \frac {1+\cos 90° }{2} \\[ 5pt ] &=& 0.9\times 100\times \frac {1+0 }{2} \\[ 5pt ] &=& 45 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ \alpha =180° \ \)の時，
\[
\begin{eqnarray}
V_{\mathrm {d}} \left( 180° \right) &≃& 0.9V_{\mathrm {a}}\frac {1+\cos \alpha }{2} \\[ 5pt ] &=& 0.9\times 100\times \frac {1+\cos 180° }{2} \\[ 5pt ] &=& 0.9\times 100\times \frac {1-1 }{2} \\[ 5pt ] &=& 0 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。この条件を満たすグラフは(5)となる。