《機械》〈電熱〉[R3:問17]熱の伝わり方及び熱力学のオームの法則に関する空欄穴埋・計算問題

【問題】

【難易度】★★★☆☆（普通）

熱の伝わり方について，次の(a)及び(b)の問に答えよ。

(a)　\( \ \fbox {　 （ア） 　} \ \)は，熱媒体を必要とせず，真空中でも熱を伝達する。高温側で温度\( \ T_{\mathrm {2}} \ \mathrm {[K]} \ \)の面\( \ S_{\mathrm {2}} \ \mathrm {[m^{2}]} \ \)と，低温側で温度\( \ T_{\mathrm {1}} \ \mathrm {[K]} \ \)の面\( \ S_{\mathrm {1}} \ \mathrm {[m^{2}]} \ \)が向かい合う場合の熱流\( \ \mathit {\Phi } \ \mathrm {[W]} \ \)は，\( \ S_{\mathrm {2}}F_{\mathrm {21}}\sigma \ （ \ \fbox {　 （イ） 　} \ ） \ \)で与えられる。

ただし，\( \ F_{\mathrm {21}} \ \)は，\( \ \fbox {　 （ウ） 　} \ \)である。また，\( \ \sigma \ \mathrm {[W / \left( m^{2}\cdot K^{4}\right) ]} \ \)は，\( \ \fbox {　 （エ） 　} \ \)定数である。

上記の記述中の空白箇所(ア)～(エ)に当てはまる組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。
\[
\begin{array}{ccccc}
& （ア） & （イ） & （ウ） & （エ） \\
\hline
(1) & 　熱伝導　 & 　T_{2}^{2}-T_{1}^{2}　 & 　形状係数　 & 　プランク　 \\
\hline
(2) & 　熱放射　 & 　T_{2}^{2}-T_{1}^{2}　 & 　形態係数　 & 　ステファン・ボルツマン　 \\
\hline
(3) & 　熱放射　 & 　T_{2}^{4}-T_{1}^{4}　 & 　形態係数　 & 　ステファン・ボルツマン　 \\
\hline
(4) & 　熱伝導　 & 　T_{2}^{4}-T_{1}^{4}　 & 　形状係数　 & 　プランク　 \\
\hline
(5) & 　熱伝導　 & 　T_{2}^{4}-T_{1}^{4}　 & 　形状係数　 & 　ステファン・ボルツマン　 \\
\hline
\end{array}
\]

(b)　下面温度が\( \ 350 \ \mathrm {K} \ \)，上面温度が\( \ 270 \ \mathrm {K} \ \)に保たれている直径\( \ 1 \ \mathrm {m} \ \)，高さ\( \ 0.1 \ \mathrm {m} \ \)の円柱がある。伝導によって円柱の高さ方向に流れる熱流\( \ \mathit {\Phi } \ \)の値\( \ \mathrm {[W]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし，円柱の熱伝導率は\( \ 0.26 \ \mathrm {W / \left( m\cdot K\right) } \ \)とする。また，円柱側面からのその他の熱の伝達及び損失はないものとする。

　(1)　\( \ 3 \ \)　　(2)　\( \ 39 \ \)　　(3)　\( \ 163 \ \)　　(4)　\( \ 653 \ \)　　(5)　\( \ 2 \ 420 \ \)

【ワンポイント解説】

放射伝熱に関する問題です。
電験としては少し難易度が高めの問題ですが，平成25年問17にほぼ同じ問題が出題されているため，過去問をしっかりと勉強された方は得点できた問題ではないかと考えられるため，難易度は普通としています。

1.熱力学におけるオームの法則
物体の温度差を\( \ \theta \ \mathrm {[K]} \ \)，熱抵抗を\( \ R \ \mathrm {[K / W]} \ \)とすると，物体の熱流\( \ I \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
I &=& \frac {\theta }{R} \\[ 5pt ] \end{eqnarray}
\] となります。

2.物体の熱抵抗\( \ R \ \mathrm {[K / W]} \ \)
物体の熱伝導率が\( \ \lambda \ \mathrm {[W / (m\cdot K )]} \ \)，断面積が\( \ S \ \mathrm {[m^{2}]} \ \)，長さが\( \ l \ \mathrm {[m]} \ \)であるとき，物体の熱抵抗\( \ R \ \mathrm {[K / W]} \ \)は，
\[
\begin{eqnarray}
R &=& \frac {l}{\lambda S} \\[ 5pt ] \end{eqnarray}
\] となります。

3.ステファン・ボルツマンの法則
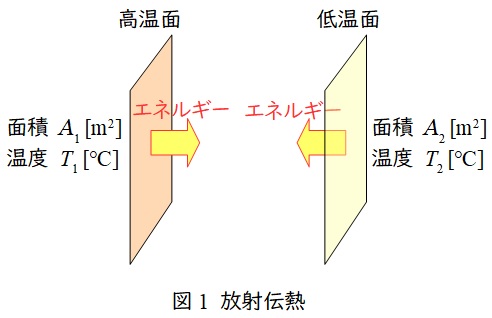
図1のように，面積\( \ A_{1} \ \mathrm {[m^{2}]} \ \)，温度\( \ T_{1} \ \mathrm {[K]} \ \)の高温面と，面積\( \ A_{2} \ \mathrm {[m^{2}]} \ \)，温度\( \ T_{2} \ \mathrm {[K]} \ \)の低温面があるとき，\( \ 1 \ \)秒当たりに高温面から低温面に伝わるエネルギー\( \ \mathit {\Phi } \ \mathrm {[W]} \ \)は，\( \ \varepsilon \ \)を放射率，\( \ \sigma \ \mathrm {[W / \left( m^{2}\cdot K^{4}\right) ]} \ \)をステファン・ボルツマン定数，\( \ F_{12} \ \)を形態係数とすると，
\[
\begin{eqnarray}
\mathit {\Phi } &=& \varepsilon \sigma A_{1}F_{12}\left( T_{1}^{4}-T_{2}^{4}\right) \\[ 5pt ] \end{eqnarray}
\] で求められます。

【解答】

(a)解答：(3)
(ア)
ワンポイント解説「3.ステファン・ボルツマンの法則」で示している通り，空間中を伝わる熱の伝わり方は熱放射となります。熱伝導は，設問(b)のような物体内を伝わる熱の伝わり方を示したものです。

(イ)
ワンポイント解説「3.ステファン・ボルツマンの法則」の通り，熱流\( \ \mathit {\Phi } \ \mathrm {[W]} \ \)は，\( \ S_{\mathrm {2}}F_{\mathrm {21}}\sigma \left( T_{2}^{4}-T_{1}^{4}\right) \ \)で求められます。

(ウ)
ワンポイント解説「3.ステファン・ボルツマンの法則」の通り，\( \ F_{\mathrm {21}} \ \)を形態係数といい，熱を伝わる物体同士の位置関係を数値化したものとなります。

(エ)
ワンポイント解説「3.ステファン・ボルツマンの法則」の通り，\( \ \sigma \ \mathrm {[W / \left( m^{2}\cdot K^{4}\right) ]} \ \)は，ステファン・ボルツマン定数と呼ばれ，約\( \ 5.67\times 10^{-8} \ \mathrm {[W / \left( m^{2}\cdot K^{4}\right) ]} \ \)である定数です。

(b)解答：(3)
円柱上面及び下面の断面積\( \ S \ \mathrm {[m^{2}]} \ \)は，直径\( \ D=1 \ \mathrm {[m]} \ \)であるから，
\[
\begin{eqnarray}
S &=& \pi \left( \frac {D}{2}\right) ^{2} \\[ 5pt ] &=& \pi \times \left( \frac {1}{2}\right) ^{2} \\[ 5pt ] &≒& 0.7854 \ \mathrm {[m^{2}]} \\[ 5pt ] \end{eqnarray}
\] となり，ワンポイント解説「2.物体の熱抵抗\( \ R \ \mathrm {[K / W]} \ \)」の通り，円柱の熱抵抗\( \ R \ \mathrm {[K / W]} \ \)は，熱伝導率\( \ \lambda =0.26 \ \mathrm {[W / \left( m\cdot K\right) ]} \ \)，高さ\( \ l=0.1 \ \mathrm {[m]} \ \)であるから，
\[
\begin{eqnarray}
R &=& \frac {l}{\lambda S} \\[ 5pt ] &=& \frac {0.1}{0.26\times 0.7854} \\[ 5pt ] &≒& 0.4897 \ \mathrm {[K / W]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，ワンポイント解説「1.熱力学におけるオームの法則」の通り，熱流\( \ \mathit {\Phi } \ \mathrm {[W]} \ \)は，温度差\( \ \theta =350-270 =80 \ \mathrm {[K]} \ \)であるから，
\[
\begin{eqnarray}
\mathit {\Phi } &=& \frac {\theta }{R} \\[ 5pt ] &=& \frac {80}{0.4897} \\[ 5pt ] &≒& 163 \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] と求められる。