《機械》〈変圧器〉[H29:問7]結線方法が異なる変圧器の角変位に関する論説問題

【問題】

【難易度】★★★☆☆（普通）

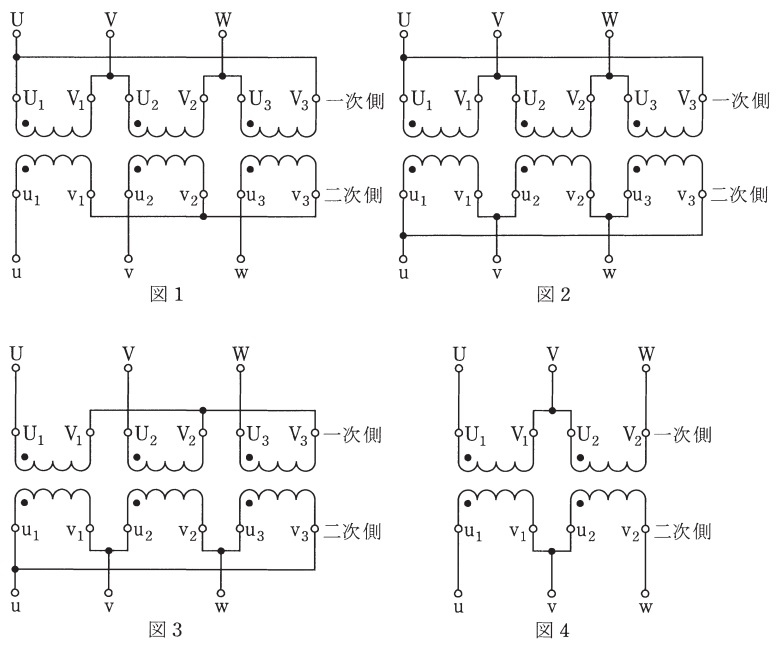
図1～3は，同じ定格の単相変圧器\( \ 3 \ \)台を用いた三相の変圧器であり，図4は，同じ定格の単相変圧器\( \ 2 \ \)台を用いた\( \ \mathrm {V} \ \)結線三相変圧器である。各図の一次側電圧に対する二次側電圧の位相変位(角変位)の値\( \ \mathrm {[rad]} \ \)の組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。
ただし，各図において一次電圧の相順は\( \ \mathrm {U} \ \)，\( \ \mathrm {V} \ \)，\( \ \mathrm {W} \ \)とする。

\[
\begin{array}{ccccc}
& 　図1　 & 　図2　 & 　図3　 & 　図4　 \\
\hline
(1) & 進み\displaystyle \frac {\pi }{6} & 0 & 遅れ\displaystyle \frac {\pi }{6} & 0 \\
\hline
(2) & 遅れ\displaystyle \frac {\pi }{6} & 0 & 進み\displaystyle \frac {\pi }{6} & 進み\displaystyle \frac {\pi }{6} \\
\hline
(3) & 遅れ\displaystyle \frac {\pi }{6} & 0 & 進み\displaystyle \frac {\pi }{6} & 0 \\
\hline
(4) & 進み\displaystyle \frac {\pi }{6} & 進み\displaystyle \frac {\pi }{6} & 遅れ\displaystyle \frac {\pi }{6} & 遅れ\displaystyle \frac {\pi }{6} \\
\hline
(5) & 遅れ\displaystyle \frac {\pi }{6} & 進み\displaystyle \frac {\pi }{6} & 進み\displaystyle \frac {\pi }{6} & 進み\displaystyle \frac {\pi }{6} \\
\hline
\end{array}
\]

【ワンポイント解説】

変圧器で角変位が発生するのは\( \ \Delta – \mathrm {Y} \ \)結線と\( \ \mathrm {Y}- \Delta \ \)結線の時です。どちらが進みか遅れかわからなくなった場合でも，ベクトル図を描いて導出できるようにしておいた方が良いでしょう。

1.\( \ \Delta – \mathrm {Y} \ \)結線の電圧の角変位
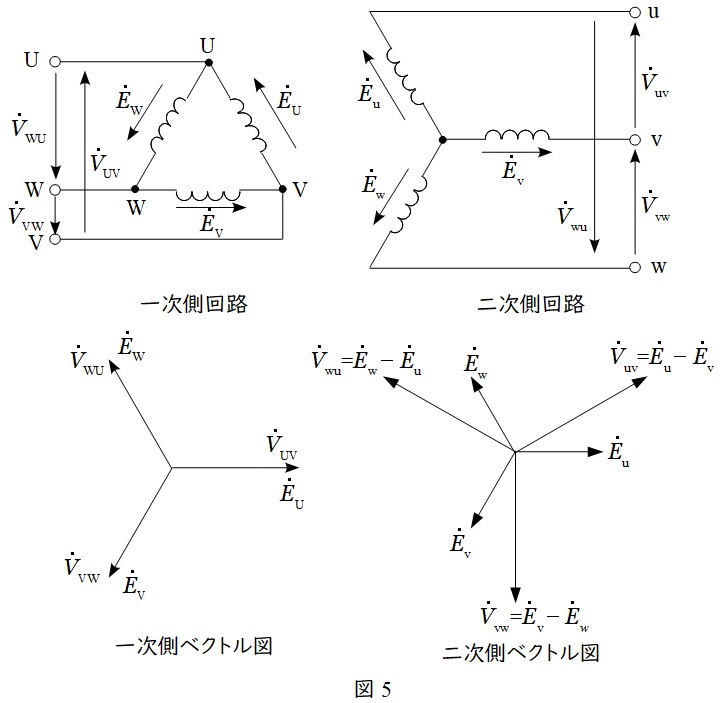
一次側\( \ \Delta \ \)，二次側\( \ \mathrm {Y} \ \)の回路図とベクトル図を描くと図5のようになります。各部の電圧は図の通りです。
一次側の相電圧\( \ E_{\mathrm {U}} \ \)，\( \ E_{\mathrm {V}} \ \)，\( \ E_{\mathrm {W}} \ \)と一次側の線間電圧\( \ V_{\mathrm {UV}} \ \)，\( \ V_{\mathrm {VW}} \ \)，\( \ V_{\mathrm {WU}} \ \)は全く同じ電圧であるので，一次側のベクトル図は図5左下のように描けます。
次に，一次側の相電圧\( \ E_{\mathrm {U}} \ \)，\( \ E_{\mathrm {V}} \ \)，\( \ E_{\mathrm {W}} \ \)と二次側の\( \ E_{\mathrm {u}} \ \)，\( \ E_{\mathrm {v}} \ \)，\( \ E_{\mathrm {w}} \ \)の位相は等しいので，二次側の\( \ E_{\mathrm {u}} \ \)，\( \ E_{\mathrm {v}} \ \)，\( \ E_{\mathrm {w}} \ \)のベクトルの向きは\( \ E_{\mathrm {U}} \ \)，\( \ E_{\mathrm {V}} \ \)，\( \ E_{\mathrm {W}} \ \)と同じになります。
また，回路図より二次側の線間電圧\( \ V_{\mathrm {uv}} \ \)，\( \ V_{\mathrm {vw}} \ \)，\( \ V_{\mathrm {wu}} \ \)は，
\[
V_{\mathrm {uv}}=E_{\mathrm {u}}-E_{\mathrm {v}}，V_{\mathrm {vw}}=E_{\mathrm {v}}-E_{\mathrm {w}}，V_{\mathrm {wu}}=E_{\mathrm {w}}-E_{\mathrm {u}}
\] となり，ベクトル図は図5右下のように描けます。
結果的に\( \ V_{\mathrm {uv}} \ \)は\( \ V_{\mathrm {UV}} \ \)より\( \ \displaystyle 30°\left( \frac {\pi }{6} \ \mathrm {[rad]}\right) \ \)進むことになります。

【解答】

解答：(1)
図1
一次側が\( \ \Delta \ \)巻線，二次側が\( \ \mathrm {Y} \ \)巻線となっているので，二次側は\( \ \displaystyle \frac {\pi }{6} \ \)進みになります。
図2
一次側も二次側も\( \ \Delta \ \)巻線になっているので，角変位はありません。
図3
一次側が\( \ \mathrm {Y} \ \)巻線，二次側が\( \ \Delta \ \)巻線となっているので，二次側は\( \ \displaystyle \frac {\pi }{6} \ \)遅れになります。
図4
一次側も二次側も\( \ \mathrm {V} \ \)結線になっているので，角変位はありません。