《機械》〈変圧器〉[R2:問9]誘導性負荷を接続した三相三巻線変圧器の供給電流に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

一次線間電圧が\( \ 66 \ \mathrm {kV} \ \)，二次線間電圧が\( \ 6.6 \ \mathrm {kV} \ \)，三次線間電圧が\( \ 3.3 \ \mathrm {kV} \ \)の三相三巻線変圧器がある。一次巻線には線間電圧\( \ 66 \ \mathrm {kV} \ \)の三相交流電源が接続されている。二次巻線に力率\( \ 0.8 \ \)，\( \ 8 \ 000 \ \mathrm {kV\cdot A} \ \)の三相誘導性負荷を接続し，三次巻線に\( \ 4 \ 800 \ \mathrm {kV\cdot A} \ \)の三相コンデンサを接続した。一次電流の値\( \ \mathrm {[A]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。ただし，変圧器の漏れインピーダンス，励磁電流及び損失は無視できるほど小さいものとする。

　(1)　\( \ 42.0 \ \)　　(2)　\( \ 56.0 \ \)　　(3)　\( \ 70.0 \ \)　　(4)　\( \ 700.0 \ \)　　(5)　\( \ 840.0 \ \)

【ワンポイント解説】

内容は電力科目や法規科目で出題されやすい電力の計算問題ですが，一般的に受電端に設けることが多い電力用コンデンサを三次巻線に設けた少しひねった問題です。
三次巻線があることで，少し驚いてしまうかもしれませんが，電圧が違うのみで内容は同じなので，十分に解ける問題になるかと思います。

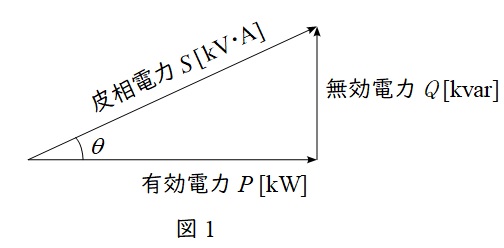
1.有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)
抵抗で消費される電力を有効電力\( \ P \ \mathrm {[W]} \ \)とリアクタンスで消費もしくは供給される電力を無効電力\( \ Q \ \mathrm {[var]} \ \)と呼び，図1のようにベクトル図を描きます。さらに，有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)のベクトル和は皮相電力\( \ S \ \mathrm {[V\cdot A]} \ \)と呼ばれ，
\[
\begin{eqnarray}
S&=&\sqrt {P^{2}+Q^{2}} \\[ 5pt ] \end{eqnarray}
\] の関係があります。図1において，力率は\( \ \cos \theta \ \)で定義され，
\[
\begin{eqnarray}
\cos \theta &=&\frac {P}{S} \\[ 5pt ] \end{eqnarray}
\] となります。

2.三相\( \ 3 \ \)線式送電線路の送電電力
三相\( \ 3 \ \)線式送電線路の線間電圧が\( \ V \ \mathrm {[V]} \ \)，線電流が\( \ I \ \mathrm {[A]} \ \)，力率が\( \ \cos \theta \ \)であるとき，皮相電力\( \ S \ \mathrm {[V\cdot A]} \ \)，有効電力\( \ P \ \mathrm {[W]} \ \)，無効電力\( \ Q \ \mathrm {[var]} \ \)はそれぞれ，
\[
\begin{eqnarray}
S &=&\sqrt {3}VI \\[ 5pt ] P &=&\sqrt {3}VI\cos \theta \\[ 5pt ] Q &=&\sqrt {3}VI\sin \theta \\[ 5pt ] &=&\sqrt {3}VI\sqrt {1-\cos ^{2}\theta } \\[ 5pt ] \end{eqnarray}
\] で求められます。

3.変圧器の巻数比と変圧比，変流比の関係
変圧器の一次側の巻数\( \ N_{1} \ \)，電圧\( \ V_{1} \ \mathrm {[V]} \ \)，電流\( \ I_{1} \ \mathrm {[A]} \ \)，二次側の巻数\( \ N_{2} \ \)，電圧\( \ V_{2} \ \mathrm {[V]} \ \)，電流\( \ I_{2} \ \mathrm {[A]} \ \)とすると，それぞれの関係は，
\[
\begin{eqnarray}
\frac {N_{1}}{N_{2}} &=&\frac {V_{1}}{V_{2}}=\frac {I_{2}}{I_{1}} \\[ 5pt ] \end{eqnarray}
\] となります。

【関連する「電気の神髄」記事】

　　有効電力・無効電力・複素電力

【解答】

解答：(2)
題意に沿って，各電圧・電力の関係を図に示すと，図2のようになる。
負荷を流れる電流\( \ I_{2} \ \mathrm {[A]} \ \)の大きさは，ワンポイント解説「2.三相\( \ 3 \ \)線式送電線路の送電電力」より，
\[
\begin{eqnarray}
I_{2} &=&\frac {S_{2}}{\sqrt {3}V_{2}} \\[ 5pt ] &=&\frac {8000\times 10^{3}}{\sqrt {3}\times 6.6\times 10^{3}} \\[ 5pt ] &≒&699.8 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となり，三次側のコンデンサを流れる電流\( \ I_{3} \ \mathrm {[A]} \ \)の大きさは，
\[
\begin{eqnarray}
I_{3} &=&\frac {S_{3}}{\sqrt {3}V_{3}} \\[ 5pt ] &=&\frac {4800\times 10^{3}}{\sqrt {3}\times 3.3\times 10^{3}} \\[ 5pt ] &≒&839.8 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となるので，ワンポイント解説「3.変圧器の巻数比と変圧比，変流比の関係」より，それぞれ一次側に換算すると，
\[
\begin{eqnarray}
I_{2}^{\prime } &=&\frac {V_{2}}{V_{1}}I_{2} \\[ 5pt ] &=&\frac {6.6\times 10^{3}}{66\times 10^{3}}\times 699.8 \\[ 5pt ] &=&69.98 \ \mathrm {[A]} \\[ 5pt ] I_{3}^{\prime } &=&\frac {V_{3}}{V_{1}}I_{3} \\[ 5pt ] &=&\frac {3.3\times 10^{3}}{66\times 10^{3}}\times 839.8 \\[ 5pt ] &=&41.99 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。\( \ I_{2}^{\prime } \ \)は遅れ力率\( \ 0.8 \ \)の電流なので，有効分と無効分に分けると，
\[
\begin{eqnarray}
{\dot I}_{2}^{\prime } &=&I_{2}^{\prime }\left( \cos \theta -\mathrm {j}\sin \theta \right) \\[ 5pt ] &=&I_{2}^{\prime }\left( \cos \theta -\mathrm {j}\sqrt {1-\cos ^{2}\theta } \right) \\[ 5pt ] &=&69.98\times \left( 0.8 -\mathrm {j}\sqrt {1-0.8 ^{2}} \right) \\[ 5pt ] &=&69.98\times \left( 0.8 -\mathrm {j}0.6 \right) \\[ 5pt ] &≒&55.98-\mathrm {j}41.99 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となるから，無効電流分がすべて\( \ I_{3}^{\prime } \ \)と相殺され零になるので，一次電流は\( \ 55.98≒56.0 \ \mathrm {[A]} \ \)と求められる。

【別解】
図2において，二次側の負荷の有効電力\( \ P_{2} \ \mathrm {[kW]} \ \)，無効電力\( \ Q_{2} \ \mathrm {[kvar]} \ \)はそれぞれ，
\[
\begin{eqnarray}
P_{2} &=&S_{2}\cos \theta \\[ 5pt ] &=&8000 \times 0.8 \\[ 5pt ] &=&6400 \ \mathrm {[kW]} \\[ 5pt ] Q_{2} &=&S_{2}\sin \theta \\[ 5pt ] &=&S_{2}\sqrt {1-\cos ^{2}\theta } \\[ 5pt ] &=&8000 \times\sqrt {1-0.8^{2}} \\[ 5pt ] &=&8000 \times 0.6 \\[ 5pt ] &=&4800 \ \mathrm {[kvar]} \\[ 5pt ] \end{eqnarray}
\] となる。無効電力\( \ Q_{2} \ \mathrm {[kvar]} \ \)は遅れ無効電力であり，三次側の無効電力\( \ Q_{\mathrm {C}} \ \mathrm {[kvar]} \ \)と大きさが等しいので，一次側の電源が供給する電力は有効電力分のみでありその大きさ\( \ P_{1} \ \mathrm {[kW]} \ \)は，
\[
\begin{eqnarray}
P_{1} &=&P_{2} \\[ 5pt ] &=&6400 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，一次側の電流\( \ I_{1} \ \mathrm {[A]} \ \)は，一次側の力率が\( \ 1 \ \)であることに注意すると，ワンポイント解説「2.三相\( \ 3 \ \)線式送電線路の送電電力」より，
\[
\begin{eqnarray}
P_{1} &=&\sqrt {3}V_{1}I_{1}\cos \theta \\[ 5pt ] I_{1} &=&\frac {P_{1}}{\sqrt {3}V_{1}\cos \theta } \\[ 5pt ] &=&\frac {6400\times 10^{3}}{\sqrt {3}\times 66 \times 10^{3}\times 1 } \\[ 5pt ] &≒&56.0 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。