《機械》〈回転機〉[H27:問4]同期発電機の端子電圧に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

定格電圧，定格電流，力率\( \ 1.0 \ \)で運転中の三相同期発電機がある。百分率同期インピーダンスは\( \ 85 \ ％ \ \)である。励磁電流を変えないで無負荷にしたとき，この発電機の端子電圧は定格電圧の何倍になるか。最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし，電機子巻線抵抗と磁気飽和は無視できるものとする。

(1)　\( \ 1.0 \ \)　　(2)　\( \ 1.1 \ \)　　(3)　\( \ 1.2 \ \)　　(4)　\( \ 1.3 \ \)　　(5)　\( \ 1.4 \ \)

【ワンポイント解説】

本問はまず等価回路とベクトル図を描き，回路計算と同様に考えられるようにして解くことが重要です。同期発電機の等価回路はそれほど難しくなく，電験では巻線抵抗や磁気飽和は無視した等価回路を描くことが基本です。各電動機の等価回路を描けるようにしておきましょう。

【解答】

解答：(4)
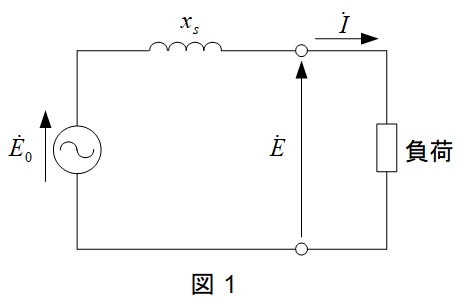
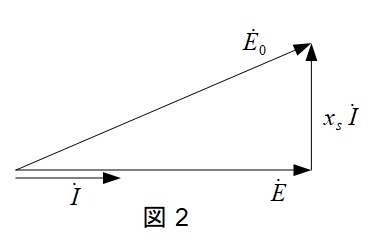
定格電圧，定格電流，力率\( \ 1.0 \ \)(端子電圧\( \ \dot {E} \ \)と電流\( \ \dot I \ \)は同位相)での等価回路とベクトル図を描くと図1，図2の通りとなる。図2において，\( \ \left|\dot I\right| =100 \ \mathrm {[％]} \ \)であるから，
\[
\begin{eqnarray}
x_{\mathrm {s}}I&=&85 \ [％] \end{eqnarray}
\] となるので，誘導起電力の大きさ\( \ E_{0} \ \)は，
\[
\begin{eqnarray}
E_{0}&=&\sqrt {E^{2}+(x_{\mathrm {s}}I) ^{2}} \\[ 5pt ] &=&\sqrt {100^{2}+85 ^{2}} \\[ 5pt ] &≒&131 \ [％] \\[ 5pt ] \end{eqnarray}
\] となる。ここで，励磁電流を変えないで無負荷にすると電流が流れず，\( \ x_{\mathrm {s}} \ \)での電圧降下が零となるので，端子電圧と誘導起電力が等しくなる。
よって，この時の端子電圧の大きさは，
\[
\begin{eqnarray}
\frac {131}{100}&≒&1.3
\end{eqnarray}
\] と求められる。

【本問に関する質疑応答】

　　励磁電流を変えないってどういう意味？