【問題】
【難易度】★★★☆☆(普通)
次の文章は,バイポーラトランジスタに関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
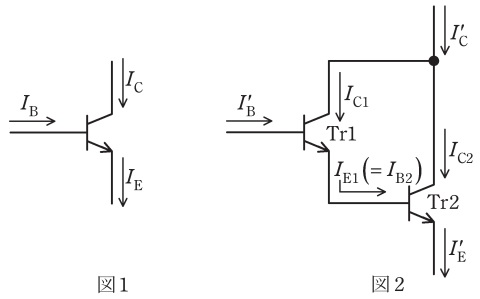
バイポーラトランジスタの各端子を流れる電流を図1のように定義するとき,コレクタ電流\( \ I_{\mathrm {C}} \ \)とエミッタ電流\( \ I_{\mathrm {E}} \ \)及びベース電流\( \ I_{\mathrm {B}} \ \)の間には,
\[
\begin{eqnarray}
I_{\mathrm {C}} &=&\alpha I_{\mathrm {E}} &・・・・・・・・・・・・・・・・・・・・・・・・ ①& \\[ 5pt ]
I_{\mathrm {C}} &=&\beta I_{\mathrm {B}} &・・・・・・・・・・・・・・・・・・・・・・・・ ②& \\[ 5pt ]
\end{eqnarray}
\]
の関係がある。ここで\( \ \alpha \ \)と\( \ \beta \ \)はそれぞれベース接地電流増幅率とエミッタ接地電流増幅率である。バイポーラトランジスタの\( \ \alpha \ \)の大きさは\( \ \fbox { (1) } \ \)。トランジスタを流れる電流は,
\[
\begin{eqnarray}
I_{\mathrm {E}} &=&I_{\mathrm {B}}+I_{\mathrm {C}} &・・・・・・・・・・・・・・・・・・・・・・ ③& \\[ 5pt ]
\end{eqnarray}
\]
であるから,エミッタ電流\( \ I_{\mathrm {E}} \ \)をベース電流\( \ I_{\mathrm {B}} \ \)と\( \ \alpha \ \)を用いて表すと,
\[
\begin{eqnarray}
I_{\mathrm {E}} &=& \ \fbox { (2) } \ I_{\mathrm {B}} &・・・・・・・・・・・・・・・・・・・・ ④& \\[ 5pt ]
\end{eqnarray}
\]
となる。①式,②式及び④式より,\( \ \alpha \ \)は\( \ \beta \ \)を用いて,
\[
\begin{eqnarray}
\alpha &=& \ \fbox { (3) } &・・・・・・・・・・・・・・・・・・・・・・ ⑤& \\[ 5pt ]
\end{eqnarray}
\]
とかける。
次に,図2に示す回路の\( \ \displaystyle \frac {I_{\mathrm {C}}^{\prime }}{I_{\mathrm {B}}^{\prime }} \ \)を求める。このとき\( \ \mathrm {Tr1} \ \)及び\( \ \mathrm {Tr2} \ \)のベース接地電流増幅率はそれぞれ\( \ \alpha _{1} \ \)及び\( \ \alpha _{2} \ \)であり,エミッタ接地電流増幅率を\( \ \beta _{1} \ \)及び\( \ \beta _{2} \ \)とすると,
\[
\begin{eqnarray}
\frac {I_{\mathrm {C}}^{\prime }}{I_{\mathrm {B}}^{\prime }} &=& \frac {I_{\mathrm {C1}}+I_{\mathrm {C2}}}{I_{\mathrm {B}}^{\prime }}=\beta _{1}+\beta _{2}\frac {I_{\mathrm {B2}}}{I_{\mathrm {B}}^{\prime }}=\beta _{1}+\beta _{2}\frac {I_{\mathrm {E1}}}{I_{\mathrm {B}}^{\prime }} &・・・・・ ⑥& \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで\( \ \mathrm {Tr1} \ \)に④式及び⑤式の関係を考慮すると,
\[
\begin{eqnarray}
\frac {I_{\mathrm {C}}^{\prime }}{I_{\mathrm {B}}^{\prime }} &=& \ \fbox { (4) } &・・・・・・・・・・・・・・・・・・・・・ ⑦& \\[ 5pt ]
\end{eqnarray}
\]
が得られる。図2の接続はダーリントン接続と呼ばれ,図2は⑦式で表される大きなエミッタ接地電流増幅率を有する等価的なトランジスタとして用いられる。図2の回路についても等価的なエミッタ接地電流増幅率\( \ \beta ^{\prime } \ \)とベース接地電流増幅率\( \ \alpha ^{\prime } \ \)の間には⑤式の関係が成り立つ,このことから,図2の回路の等価的なベース接地電流増幅率\( \ \alpha ^{\prime } \ \)は\( \ \alpha _{1} \ \)及び\( \ \alpha _{2} \ \)を用いて,
\[
\begin{eqnarray}
\alpha ^{\prime } &=& \frac {I_{\mathrm {C}}^{\prime }}{I_{\mathrm {E}}^{\prime }}= \ \fbox { (5) } \\[ 5pt ]
\end{eqnarray}
\]
とかける。
〔問7の解答群〕
\[
\begin{eqnarray}
&(イ)& ちょうど \ 1 \ である &(ロ)& 1 \ より大きい &(ハ)& 1 \ より小さい \\[ 5pt ]
&(ニ)& \frac {\alpha _{1}\alpha _{2}}{\left( 1-\alpha _{1}\right) \left( 1-\alpha _{2}\right) } &(ホ)& \frac {\beta }{1+\beta } &(ヘ)& \beta _{1}+\beta _{2} \\[ 5pt ]
&(ト)& \frac {\beta }{\beta -1} &(チ)& 2\beta _{1}\beta _{2} &(リ)& \beta _{1}+\beta _{2}+\beta _{1}\beta _{2} \\[ 5pt ]
&(ヌ)& 1-\alpha &(ル)& \frac {1}{1-\alpha } &(ヲ)& \alpha _{1}+\alpha _{2}-\alpha _{1}\alpha _{2} \\[ 5pt ]
&(ワ)& \frac {1}{\alpha -1} &(カ)& \frac {1}{1-\beta } &(ヨ)& \frac {\alpha _{1}}{1-\alpha _{1}}+\frac {\alpha _{2}}{1-\alpha _{2}} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
バイポーラトランジスタを\( \ 2 \ \)個接続した回路における電流増幅率に関する問題です。
出題内容は基礎的な内容ですが,(5)の計算量が多く\( \ 1 \ \)種らしい問題と言えると思います。
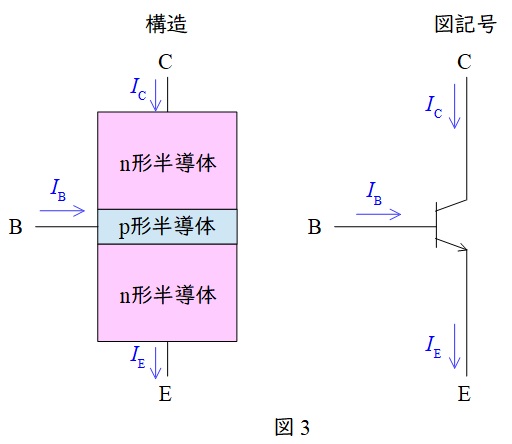
1.\( \ \mathrm {npn} \ \)バイポーラトランジスタの構造と動作
図3のように\( \ \mathrm {npn} \ \)バイポーラトランジスタは,\( \ 2 \ \)つの\( \ \mathrm {n} \ \)形半導体の間に\( \ \mathrm {p} \ \)形半導体を挟んだサンドイッチ構造となっています。
\( \ \mathrm {npn} \ \)バイポーラトランジスタに\( \ V_{\mathrm {E}}<V_{\mathrm {C}} \ \)となる電圧をかけ,さらに\( \ V_{\mathrm {E}}<V_{\mathrm {B}}<V_{\mathrm {C}} \ \)の電圧をかけベース電流\( \ I_{\mathrm {B}} \ \)を流すと,トランジスタはオンし,ベースとコレクタからエミッタへ電流が流れます。通常ベース電流\( \ I_{\mathrm {B}} \ \)はコレクタ電流\( \ I_{\mathrm {C}} \ \)より十分に小さいためコレクタ電流\( \ I_{\mathrm {C}} \ \)とエミッタ電流\( \ I_{\mathrm {E}} \ \)はほぼ等しいと考えます。
\[
\begin{eqnarray}
I_{\mathrm {E}} &=&I_{\mathrm {B}}+I_{\mathrm {C}} \\[ 5pt ]
&≒&I_{\mathrm {C}} \\[ 5pt ]
\end{eqnarray}
\]
また,ベース電流\( \ I_{\mathrm {B}} \ \)を流すのを止めるとトランジスタはオフし,コレクタ電流\( \ I_{\mathrm {C}} \ \)が流れなくなります。
【解答】
(1)解答:ハ
ワンポイント解説「1.\( \ \mathrm {npn} \ \)バイポーラトランジスタの構造と動作」の通り,
\[
\begin{eqnarray}
I_{\mathrm {E}} &=&I_{\mathrm {B}}+I_{\mathrm {C}} \\[ 5pt ]
\end{eqnarray}
\]
であり,\( \ I_{\mathrm {E}} > I_{\mathrm {C}} \ \)であるため,\( \ \alpha \ \)は\( \ 1 \ \)より小さい。
(2)解答:ル
①を③に代入すると,
\[
\begin{eqnarray}
I_{\mathrm {E}} &=&I_{\mathrm {B}}+\alpha I_{\mathrm {E}} \\[ 5pt ]
\left( 1-\alpha \right) I_{\mathrm {E}} &=&I_{\mathrm {B}} \\[ 5pt ]
I_{\mathrm {E}} &=&\frac {1}{1-\alpha }I_{\mathrm {B}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ホ
②を①に代入すると,
\[
\begin{eqnarray}
\beta I_{\mathrm {B}} &=&\alpha I_{\mathrm {E}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,これに④を代入すると,
\[
\begin{eqnarray}
\beta I_{\mathrm {B}} &=&\alpha \frac {1}{1-\alpha }I_{\mathrm {B}} \\[ 5pt ]
\beta &=&\frac {\alpha }{1-\alpha } ・・・・・・・・・・・・・・・ ⑧ \\[ 5pt ]
\left( 1-\alpha \right) \beta &=&\alpha \\[ 5pt ]
\beta -\alpha \beta &=&\alpha \\[ 5pt ]
\left( 1+\beta \right) \alpha &=&\beta \\[ 5pt ]
\alpha &=&\frac {\beta }{1+\beta } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:リ
⑥において,④の関係式を代入すると,
\[
\begin{eqnarray}
\frac {I_{\mathrm {C}}^{\prime }}{I_{\mathrm {B}}^{\prime }} &=&\beta _{1}+\beta _{2}\frac {I_{\mathrm {E1}}}{I_{\mathrm {B}}^{\prime }} \\[ 5pt ]
&=&\beta _{1}+\beta _{2}\frac {1}{1-\alpha _{1}} \\[ 5pt ]
\end{eqnarray}
\]
となり,⑤の関係式を代入すると,
\[
\begin{eqnarray}
\frac {I_{\mathrm {C}}^{\prime }}{I_{\mathrm {B}}^{\prime }} &=&\beta _{1}+\beta _{2}\frac {1}{\displaystyle 1-\frac {\beta _{1}}{1+\beta _{1}} } \\[ 5pt ]
&=&\beta _{1}+\beta _{2}\frac {1}{\displaystyle \frac {1}{1+\beta _{1}} } \\[ 5pt ]
&=&\beta _{1}+\beta _{2}\left( 1+\beta _{1}\right) \\[ 5pt ]
&=&\beta _{1}+\beta _{2}+\beta _{1}\beta _{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ヲ
⑦においては,\( \ \beta ^{\prime }=\beta _{1}+\beta _{2}+\beta _{1}\beta _{2} \ \)と考えることができるので,これを⑤に代入すると,
\[
\begin{eqnarray}
\alpha ^{\prime } &=& \frac {\beta ^{\prime }}{1+\beta ^{\prime }} \\[ 5pt ]
&=& \frac {\beta _{1}+\beta _{2}+\beta _{1}\beta _{2}}{1+\beta _{1}+\beta _{2}+\beta _{1}\beta _{2}} \\[ 5pt ]
\end{eqnarray}
\]
となる。さらに⑧を代入すると,
\[
\begin{eqnarray}
\alpha ^{\prime } &=& \frac {\beta _{1}+\beta _{2}+\beta _{1}\beta _{2}}{1+\beta _{1}+\beta _{2}+\beta _{1}\beta _{2}} \\[ 5pt ]
&=& \frac {\displaystyle \frac {\alpha _{1}}{1-\alpha _{1}}+\frac {\alpha _{2}}{1-\alpha _{2}}+\frac {\alpha _{1}}{1-\alpha _{1}}\frac {\alpha _{2}}{1-\alpha _{2}}}{\displaystyle 1+\frac {\alpha _{1}}{1-\alpha _{1}}+\frac {\alpha _{2}}{1-\alpha _{2}}+\frac {\alpha _{1}}{1-\alpha _{1}}\frac {\alpha _{2}}{1-\alpha _{2}}} \\[ 5pt ]
&=& \frac {\alpha _{1}\left( 1-\alpha _{2}\right) +\alpha _{2}\left( 1-\alpha _{1}\right) +\alpha _{1}\alpha _{2}}{\left( 1-\alpha _{1}\right) \left( 1-\alpha _{2}\right) +\alpha _{1}\left( 1-\alpha _{2}\right) +\alpha _{2}\left( 1-\alpha _{1}\right) +\alpha _{1}\alpha _{2}} \\[ 5pt ]
&=& \frac {\alpha _{1}-\alpha _{1}\alpha _{2} +\alpha _{2}-\alpha _{1}\alpha _{2}+\alpha _{1}\alpha _{2}}{1-\alpha _{1}-\alpha _{2}+\alpha _{1}\alpha _{2} +\alpha _{1}-\alpha _{1}\alpha _{2} +\alpha _{2}-\alpha _{1}\alpha _{2}+\alpha _{1}\alpha _{2}} \\[ 5pt ]
&=& \alpha _{1}+\alpha _{2}-\alpha _{1}\alpha _{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん