【問題】
【難易度】★★☆☆☆(やや易しい)
図に示すフィードバック制御系について,次の問に答えよ。
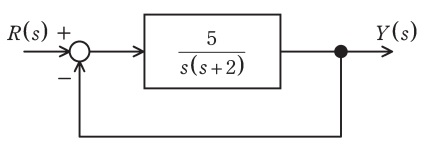
(1) 目標値\( \ R\left( s \right) \ \)から制御量\( \ Y\left( s \right) \ \)までの閉ループ伝達関数\( \ W\left( s \right) \ \)を求めよ。
(2) 閉ループ伝達関数\( \ W\left( s \right) \ \)の固有角周波数\( \ \omega _{\mathrm {n}} \ \)と減衰係数\( \ \zeta \ \)を求めよ。
(3) 目標値\( \ R\left( s \right) \ \)を\( \ t=0 \ \)で単位ステップで変化させたときの制御量の時間応答\( \ y\left( t \right) \ \)を求めよ。
必要に応じて,ラプラス変換の複素領域における推移定理である\( \ \mathcal {L} \left[ \mathrm {e}^{-at}x\left( t \right) \right] =X\left( s+a\right) \ \)を使ってよい。
(4) 小問(3)の時間応答\( \ y\left( t \right) \ \)は減衰振動となる。\( \ y\left( t \right) \ \)を時間微分し,\( \ t>0 \ \)における一つ目の極値が最大値であることを使って,時間応答\( \ y\left( t \right) \ \)が最大となる時間\( \ t_{\mathrm {p}} \ \)を求めよ。
(5) 小問(3)の時間応答\( \ y\left( t \right) \ \)の最大値\( \ y\left( t_{\mathrm {p}} \right) \ \)を求めよ。
【ワンポイント解説】
電験\( \ 1 \ \)種では珍しいオーソドックスな古典制御のフィードバック制御に関する問題です。
令和\( \ 3 \ \)年の機械制御科目の中では最も易しい問題でしたので,本問を選択された受験生がより合格に近づいたのではないかと思います。
1.基本的なラプラス変換
\( \ f(t) \ \)のラプラス変換を\( \ F(s) \ \)とすると以下のような関係があります。
\[
\begin{array}{|c|c|}
\hline
f(t) & F(s) \\
\hline
{\displaystyle \delta (t) }\atop{単位インパルス関数} & 1 \\[ 5pt ]
{\displaystyle u (t) }\atop{単位ステップ関数} & \displaystyle \frac {1}{s} \\[ 5pt ]
K & \displaystyle \frac {K}{s} \\[ 5pt ]
t & \displaystyle \frac {1}{s^{2}} \\[ 5pt ]
\mathrm {e}^{at} & \displaystyle \frac {1}{s-a} \\[ 5pt ]
\sin \omega t & \displaystyle \frac {\omega }{s^{2}+\omega ^{2}} \\[ 5pt ]
\cos \omega t & \displaystyle \frac {s}{s^{2}+\omega ^{2}} \\[ 5pt ]
\hline
\end{array}
\]
2.減衰係数\( \ \zeta \ \)と固有角周波数\( \ \omega _{\mathrm {n}} \ \)
2次遅れの伝達関数\( \ W(s) \ \)の一般式は,減衰係数\( \ \zeta \ \),固有角周波数\( \ \omega _{\mathrm {n}} \ \)とすると,
\[
\begin{eqnarray}
W(s)&=&\frac {\omega _{\mathrm {n}}^{2}}{s^{2}+2\zeta \omega _{\mathrm {n}}s+\omega _{\mathrm {n}}^{2}} \\[ 5pt ]
\end{eqnarray}
\]
で表されます。
【解答】
(1)目標値\( \ R\left( s \right) \ \)から制御量\( \ Y\left( s \right) \ \)までの閉ループ伝達関数\( \ W\left( s \right) \ \)
問題図のフィードバック制御系において,
\[
\begin{eqnarray}
\left\{ R\left( s \right) -Y\left( s \right) \right\} \cdot \frac {5}{s\left( s+2\right) }&=&Y\left( s \right) \\[ 5pt ]
\end{eqnarray}
\]
の関係があるので,整理すると,
\[
\begin{eqnarray}
\left\{ R\left( s \right) -Y\left( s \right) \right\} \cdot 5&=&s\left( s+2\right) Y\left( s \right) \\[ 5pt ]
5R\left( s \right) -5Y\left( s \right) &=&\left( s^{2}+2s\right) Y\left( s \right) \\[ 5pt ]
5R\left( s \right) &=&\left( s^{2}+2s+5\right) Y\left( s \right) \\[ 5pt ]
\frac {Y\left( s \right) }{R\left( s \right) } &=&\frac {5}{s^{2}+2s+5} \\[ 5pt ]
W\left( s \right) &=&\frac {5}{s^{2}+2s+5} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)閉ループ伝達関数\( \ W\left( s \right) \ \)の固有角周波数\( \ \omega _{\mathrm {n}} \ \)と減衰定数\( \ \zeta \ \)
ワンポイント解説「2.減衰係数\( \ \zeta \ \)と固有角周波数\( \ \omega _{\mathrm {n}} \ \)」の通り,(1)解答式と2次遅れの伝達関数\( \ W(s) \ \)の一般式を比較すると,
\[
\begin{eqnarray}
2\zeta \omega _{\mathrm {n}}&=&2 \\[ 5pt ]
\omega _{\mathrm {n}}^{2}&=&5 \\[ 5pt ]
\end{eqnarray}
\]
となるので,これを解くと,
\[
\begin{eqnarray}
\omega _{\mathrm {n}}&=&\sqrt {5} \\[ 5pt ]
2\zeta \times \sqrt {5}&=&2 \\[ 5pt ]
\zeta &=&\frac {1}{\sqrt {5}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)目標値\( \ R\left( s \right) \ \)を\( \ t=0 \ \)で単位ステップで変化させたときの制御量の時間応答\( \ y\left( t \right) \ \)
ワンポイント解説「1.基本的なラプラス変換」の通り,単位ステップ関数のラプラス変換は\( \ \displaystyle \frac {1}{s} \ \)であるから,これを(1)解答式に代入すると,
\[
\begin{eqnarray}
Y\left( s \right) &=&\frac {5}{s^{2}+2s+5}R\left( s \right) \\[ 5pt ]
&=&\frac {5}{s^{2}+2s+5}\cdot \frac {1}{s} \\[ 5pt ]
&=&\frac {5}{s\left( s^{2}+2s+5\right) } \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,\( \ \displaystyle Y\left( s \right) = \frac {A}{s}+\frac {Bs+C}{s^{2}+2s+5} \ \)とおくと,
\[
\begin{eqnarray}
\frac {A}{s}+\frac {Bs+C}{s^{2}+2s+5}&=&\frac {5}{s\left( s^{2}+2s+5\right) } \\[ 5pt ]
\frac {A\left( s^{2}+2s+5\right) +\left( Bs+C\right) s}{s\left( s^{2}+2s+5\right) } &=&\frac {5}{s\left( s^{2}+2s+5\right) } \\[ 5pt ]
\frac {\left( A+B\right) s^{2} +\left( 2A+C\right) s + 5A}{s\left( s^{2}+2s+5\right) } &=&\frac {5}{s\left( s^{2}+2s+5\right) } \\[ 5pt ]
\end{eqnarray}
\]
となるので,左辺右辺を係数比較すれば,
\[
\begin{eqnarray}
A+B&=&0 \\[ 5pt ]
2A+C &=&0 \\[ 5pt ]
5A &=&5 \\[ 5pt ]
\end{eqnarray}
\]
となり,これを解くと\( \ A=1,B=-1,C=-2 \ \)となる。これより\( \ Y\left( s \right) \ \)は,
\[
\begin{eqnarray}
Y\left( s \right) &=&\frac {1}{s}+\frac {-s-2}{s^{2}+2s+5} \\[ 5pt ]
&=&\frac {1}{s}-\frac {s+2}{\left( s+1\right) ^{2}+4} \\[ 5pt ]
&=&\frac {1}{s}-\frac {\left( s+1\right) +1}{\left( s+1\right) ^{2}+2^{2}} \\[ 5pt ]
&=&\frac {1}{s}-\frac {s+1}{\left( s+1\right) ^{2}+2^{2}}-\frac {1}{2}\cdot \frac {2}{\left( s+1\right) ^{2}+2^{2}} \\[ 5pt ]
\end{eqnarray}
\]
と変形できるので,これを逆ラプラス変換すると,
\[
\begin{eqnarray}
y\left( t \right) &=&1-\mathrm {e}^{-t}\cos 2t-\frac {1}{2}\mathrm {e}^{-t}\sin 2t \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)時間応答\( \ y\left( t \right) \ \)が最大となる時間\( \ t_{\mathrm {p}} \ \)
(3)解答式の両辺を\( \ t \ \)で微分すると,
\[
\begin{eqnarray}
\frac {\mathrm {d}y\left( t \right) }{\mathrm {d}t} &=&0-\left\{ \left( -1\right) \mathrm {e}^{-t}\cos 2t+\mathrm {e}^{-t}\cdot 2 \left( -\sin 2t\right) \right\}-\frac {1}{2}\left\{ \left( -1\right) \mathrm {e}^{-t}\sin 2t+\mathrm {e}^{-t}\cdot 2 \cos 2t \right\} \\[ 5pt ]
&=&\mathrm {e}^{-t}\cos 2t+2\mathrm {e}^{-t}\sin 2t +\frac {1}{2}\mathrm {e}^{-t}\sin 2t-\mathrm {e}^{-t}\cos 2t \\[ 5pt ]
&=&\frac {5}{2}\mathrm {e}^{-t}\sin 2t \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ y\left( t \right) \ \)が最大となる時間\( \ t_{\mathrm {p}} \ \)は,\( \ \displaystyle \frac {\mathrm {d}y\left( t \right) }{\mathrm {d}t}=0 \ \)となるときの\( \ t \ \)なので,
\[
\begin{eqnarray}
\frac {5}{2}\mathrm {e}^{-t}\sin 2t &=&0 \\[ 5pt ]
\sin 2t &=&0 \\[ 5pt ]
t&=&0,\frac {\pi }{2},\pi ,\cdots \\[ 5pt ]
\end{eqnarray}
\]
となる。題意より\( \ t>0 \ \)における一つ目の極値が最大値であるから,\( \ \displaystyle t_{\mathrm {p}}=\frac {\pi }{2} \ \)と求められる。
(5)時間応答\( \ y\left( t \right) \ \)の最大値\( \ y\left( t_{\mathrm {p}} \right) \ \)
\( \ \displaystyle t_{\mathrm {p}}=\frac {\pi }{2} \ \)を(3)解答式に代入すると,
\[
\begin{eqnarray}
y\left( t_{\mathrm {p}} \right) &=&1-\mathrm {e}^{-t_{\mathrm {p}}}\cos 2t_{\mathrm {p}}-\frac {1}{2}\mathrm {e}^{-t_{\mathrm {p}}}\sin 2t_{\mathrm {p}} \\[ 5pt ]
&=&1-\mathrm {e}^{-\frac {\pi }{2}}\cos \left( 2\cdot \frac {\pi }{2}\right) -\frac {1}{2}\mathrm {e}^{-\frac {\pi }{2}}\sin \left( 2\cdot \frac {\pi }{2}\right) \\[ 5pt ]
&=&1-\mathrm {e}^{-\frac {\pi }{2}}\cos \pi -\frac {1}{2}\mathrm {e}^{-\frac {\pi }{2}}\sin \pi \\[ 5pt ]
&=&1+\mathrm {e}^{-\frac {\pi }{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん