【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,三つの同心導体球殻\( \ \mathrm {A} \ \),\( \ \mathrm {B} \ \),\( \ \mathrm {C} \ \)上の電荷と電位に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
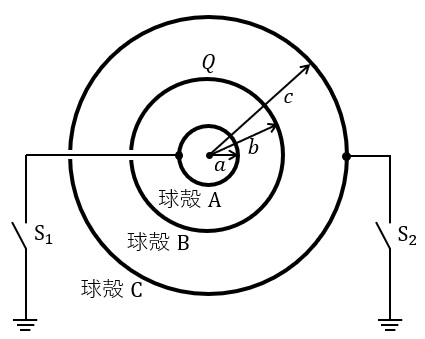
図のように,球殻\( \ \mathrm {A} \ \),\( \ \mathrm {B} \ \),\( \ \mathrm {C} \ \)は同心となるように真空中(誘電率\( \ \varepsilon _{0} \ \))に置かれている。それぞれの半径は\( \ a \ \),\( \ b \ \),\( \ c \ \)であり,球殻の厚さは無視できる。また,各球殻の初期電荷は零である。球殻\( \ \mathrm {B} \ \)及び\( \ \mathrm {C} \ \)には穴が開けられて導線が引き出されており,スイッチ\( \ \mathrm {S_{1}} \ \)を閉じることで球殻\( \ \mathrm {A} \ \)を接地できる。また,スイッチ\( \ \mathrm {S_{2}} \ \)を閉じることで球殻\( \ \mathrm {C} \ \)を接地できる。穴は十分小さく,かつ導線及びスイッチは周りの空間と絶縁されており,その影響は無視できる。
\( \ \mathrm {S_{1}} \ \)及び\( \ \mathrm {S_{2}} \ \)が共に開いている状態で,球殻\( \ \mathrm {B} \ \)に電荷\( \ Q \ \)を与える場合,無限遠を接地電位(零)としたときの球殻\( \ \mathrm {A} \ \)の電位は\( \ \fbox { (1) } \ \)となる。
\( \ \mathrm {S_{1}} \ \)のみを閉じている状態で,球殻\( \ \mathrm {B} \ \)に電荷\( \ Q \ \)を与える場合,球殻\( \ \mathrm {A} \ \)に電荷\( \ \fbox { (2) } \ \)が生じ,無限遠を接地電位(零)としたときの球殻\( \ \mathrm {B} \ \)の電位は\( \ \fbox { (3) } \ \)となる。これより,球殻\( \ \mathrm {B} \ \)の対地静電容量を\( \ \fbox { (4) } \ \)と求めることができる。
\( \ \mathrm {S_{1}} \ \)と\( \ \mathrm {S_{2}} \ \)を共に閉じている状態で球殻\( \ \mathrm {B} \ \)に電荷\( \ Q \ \)を与える場合,球殻\( \ \mathrm {C} \ \)の電荷は\( \ \fbox { (5) } \ \)となる。
〔問1の解答群〕
\[
\begin{eqnarray}
&(イ)& Q &(ロ)& -Q &(ハ)& 0 \\[ 5pt ]
&(ニ)& -\frac {\left( c-b\right) a}{\left( c-a\right) b}Q &(ホ)& \frac {\left( b-a\right) Q}{4\pi \varepsilon _{0}a^{2}} &(ヘ)& -\frac {\left( b-a\right) c}{\left( c-a\right) b}Q \\[ 5pt ]
&(ト)& 4\pi \varepsilon _{0}b &(チ)& \frac {\left( c-b\right) Q}{4\pi \varepsilon _{0}bc} &(リ)& \frac {Q}{4\pi \varepsilon _{0}b} \\[ 5pt ]
&(ヌ)& \frac {4\pi \varepsilon _{0}ab}{b-a} &(ル)& \frac {Q}{4\pi \varepsilon _{0}a} &(ヲ)& -\frac {a}{b}Q \\[ 5pt ]
&(ワ)& \frac {\left( b-a\right) Q}{4\pi \varepsilon _{0}b^{2}} &(カ)& -\frac {\left( b-a\right) b}{\left( c-a\right) c}Q &(ヨ)& \frac {4\pi \varepsilon _{0}b^{2}}{b-a} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
三つの同心導体球に電荷を加えたときの電荷や電位を求める問題です。
問題はシンプルですが,難易度は比較的高いいかにも\( \ 1 \ \)種らしい問題です。
(2)以降は内側に蓄えられる電荷を一旦\( \ Q^{\prime } \ \)とおいて解くところがポイントとなります。
1.ガウスの法則
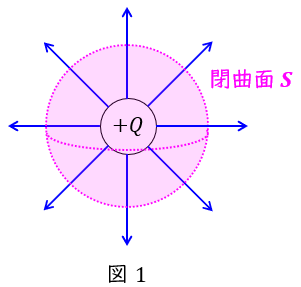
\( \ Q \ \mathrm {[C]} \ \)から出る電気力線は\( \ \displaystyle \frac {Q}{\varepsilon } \ \)本,電束は\( \ Q \ \)本であり,電界\( \ E \ \mathrm {[V / m]} \ \)及び電束密度\( \ D \ \mathrm {[C / m^{2}]} \ \)との関係は,任意の閉曲面において,
\[
\begin{eqnarray}
\int _{S} \boldsymbol E \cdot \mathrm {d}\boldsymbol S &=& \frac {Q}{\varepsilon } \\[ 5pt ]
\int _{S} \boldsymbol D \cdot \mathrm {d}\boldsymbol S &=& Q \\[ 5pt ]
\end{eqnarray}
\]
となり,これをガウスの法則といいます。閉曲面が球で,点電荷に蓄えられている電荷\( \ Q \ \mathrm {[C]} \ \)があれば,電界\( \ E \ \mathrm {[V / m]} \ \)は,
\[
\begin{eqnarray}
4\pi r^{2} \cdot E &=& \frac {Q}{\varepsilon } \\[ 5pt ]
E &=& \frac {Q}{4\pi \varepsilon r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.空間上の電位\( \ V \ \)
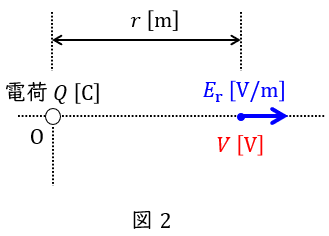
中心からの距離\( \ r \ \mathrm {[m]} \ \)に関する電界\( \ E_{\mathrm {r}} \ \mathrm {[V / m]} \ \)が与えられている時,その場所の電位\( \ V \ \mathrm {[V]} \ \)は無限遠を基準とすると,
\[
\begin{eqnarray}
V&=&-\int _{\infty }^{r}E_{\mathrm {r}}\mathrm {d}r \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
【解答】
(1)解答:リ
ワンポイント解説「1.ガウスの法則」の通り,球殻\( \ \mathrm {B} \ \)の内側の電界は\( \ 0 \ \)であり,球殻\( \ \mathrm {B} \ \)の外側の電界\( \ E_{\mathrm {r}} \ \)は,
\[
\begin{eqnarray}
4\pi r^{2}E_{\mathrm {r}} &=& \frac {Q}{\varepsilon _{0}} \\[ 5pt ]
E_{\mathrm {r}} &=& \frac {Q}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,無限遠を基準とした球殻\( \ \mathrm {A} \ \)の電位\( \ V_{\mathrm {A}} \ \)は,ワンポイント解説「2.空間上の電位\( \ V \ \)」の通り,
\[
\begin{eqnarray}
V_{\mathrm {A}}&=&-\int _{b}^{a}0\mathrm {d}r-\int _{\infty }^{b}E_{\mathrm {r}}\mathrm {d}r \\[ 5pt ]
&=&-\int _{\infty }^{b}E_{\mathrm {r}}\mathrm {d}r \\[ 5pt ]
&=&-\int _{\infty }^{b}\frac {Q}{4\pi \varepsilon _{0}r^{2}}\mathrm {d}r \\[ 5pt ]
&=&-\frac {Q}{4\pi \varepsilon _{0}}\int _{\infty }^{b}\frac {1}{r^{2}}\mathrm {d}r \\[ 5pt ]
&=&-\frac {Q}{4\pi \varepsilon _{0}}\left[ -\frac {1}{r}\right] _{\infty }^{b} \\[ 5pt ]
&=&-\frac {Q}{4\pi \varepsilon _{0}}\left( -\frac {1}{b}\right) \\[ 5pt ]
&=&\frac {Q}{4\pi \varepsilon _{0}b} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ヲ
\( \ \mathrm {S_{1}} \ \)のみを閉じているときの球殻\( \ \mathrm {A} \ \)に蓄えられる電荷を\( \ Q^{\prime } \ \)とすると,球殻\( \ \mathrm {B} \ \)の内側の電界\( \ E_{\mathrm {r1}} \ \)は,ワンポイント解説「1.ガウスの法則」の通り,
\[
\begin{eqnarray}
E_{\mathrm {r1}} &=& \frac {Q^{\prime }}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となり,球殻\( \ \mathrm {B} \ \)の外側の電界\( \ E_{\mathrm {r2}} \ \)は,
\[
\begin{eqnarray}
E_{\mathrm {r2}} &=& \frac {Q+Q^{\prime }}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,無限遠を基準とした球殻\( \ \mathrm {A} \ \)の電位\( \ V_{\mathrm {A}}^{\prime } \ \)は,ワンポイント解説「2.空間上の電位\( \ V \ \)」の通り,
\[
\begin{eqnarray}
V_{\mathrm {A}}^{\prime }&=&-\int _{b}^{a}E_{\mathrm {r1}}\mathrm {d}r-\int _{\infty }^{b}E_{\mathrm {r2}}\mathrm {d}r \\[ 5pt ]
&=&-\int _{b}^{a}\frac {Q^{\prime }}{4\pi \varepsilon _{0}r^{2}}\mathrm {d}r-\int _{\infty }^{b}\frac {Q+Q^{\prime }}{4\pi \varepsilon _{0}r^{2}}\mathrm {d}r \\[ 5pt ]
&=&-\frac {Q^{\prime }}{4\pi \varepsilon _{0}}\int _{b}^{a}\frac {1}{r^{2}}\mathrm {d}r-\frac {Q+Q^{\prime }}{4\pi \varepsilon _{0}}\int _{\infty }^{b}\frac {1}{r^{2}}\mathrm {d}r \\[ 5pt ]
&=&-\frac {Q^{\prime }}{4\pi \varepsilon _{0}}\left[ -\frac {1}{r}\right] _{b}^{a}-\frac {Q+Q^{\prime }}{4\pi \varepsilon _{0}}\left[ -\frac {1}{r}\right] _{\infty }^{b} \\[ 5pt ]
&=&-\frac {Q^{\prime }}{4\pi \varepsilon _{0}}\left( -\frac {1}{a}+\frac {1}{b}\right) -\frac {Q+Q^{\prime }}{4\pi \varepsilon _{0}}\left( -\frac {1}{b}\right) \\[ 5pt ]
&=&-\frac {1}{4\pi \varepsilon _{0}}\left( -\frac {Q^{\prime }}{a}+\frac {Q^{\prime }}{b}-\frac {Q+Q^{\prime }}{b}\right) \\[ 5pt ]
&=&-\frac {1}{4\pi \varepsilon _{0}}\left( -\frac {Q^{\prime }}{a}-\frac {Q}{b}\right) \\[ 5pt ]
&=&\frac {1}{4\pi \varepsilon _{0}}\left( \frac {Q^{\prime }}{a}+\frac {Q}{b}\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,球殻\( \ \mathrm {A} \ \)は接地されているので,\( \ V_{\mathrm {A}}^{\prime }=0 \ \)であるから,
\[
\begin{eqnarray}
\frac {1}{4\pi \varepsilon _{0}}\left( \frac {Q^{\prime }}{a}+\frac {Q}{b}\right) &=&0 \\[ 5pt ]
\frac {Q^{\prime }}{a}+\frac {Q}{b} &=&0 \\[ 5pt ]
\frac {Q^{\prime }}{a} &=&-\frac {Q}{b} \\[ 5pt ]
Q^{\prime }&=&-\frac {a}{b}Q \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ワ
(2)より,球殻\( \ \mathrm {B} \ \)の外側の電界\( \ E_{\mathrm {r2}} \ \)は,
\[
\begin{eqnarray}
E_{\mathrm {r2}} &=& \frac {Q+Q^{\prime }}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ]
&=& \frac {\displaystyle Q-\frac {a}{b}Q}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ]
&=& \frac {b-a}{b}\frac {Q}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,無限遠を基準とした球殻\( \ \mathrm {B} \ \)の電位\( \ V_{\mathrm {B}}^{\prime } \ \)は,ワンポイント解説「2.空間上の電位\( \ V \ \)」の通り,
\[
\begin{eqnarray}
V_{\mathrm {B}}^{\prime }&=&-\int _{\infty }^{b}E_{\mathrm {r2}}\mathrm {d}r \\[ 5pt ]
&=&-\int _{\infty }^{b}\frac {b-a}{b}\frac {Q}{4\pi \varepsilon _{0}r^{2}}\mathrm {d}r \\[ 5pt ]
&=&-\frac {\left( b-a\right) Q}{4\pi \varepsilon _{0}b}\int _{\infty }^{b}\frac {1}{r^{2}}\mathrm {d}r \\[ 5pt ]
&=&-\frac {\left( b-a\right) Q}{4\pi \varepsilon _{0}b}\left[ -\frac {1}{r}\right] _{\infty }^{b} \\[ 5pt ]
&=&-\frac {\left( b-a\right) Q}{4\pi \varepsilon _{0}b}\left( -\frac {1}{b}\right) \\[ 5pt ]
&=&\frac {\left( b-a\right) Q}{4\pi \varepsilon _{0}b^{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ヨ
(3)解答式より,球殻\( \ \mathrm {B} \ \)の対地静電容量\( \ C_{\mathrm {B}} \ \)は,
\[
\begin{eqnarray}
C_{\mathrm {B}}&=&\frac {Q}{V_{\mathrm {B}}^{\prime }} \\[ 5pt ]
&=&\frac {Q}{\displaystyle \frac {\left( b-a\right) Q}{4\pi \varepsilon _{0}b^{2}}} \\[ 5pt ]
&=&\frac {4\pi \varepsilon _{0}b^{2}}{b-a} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ヘ
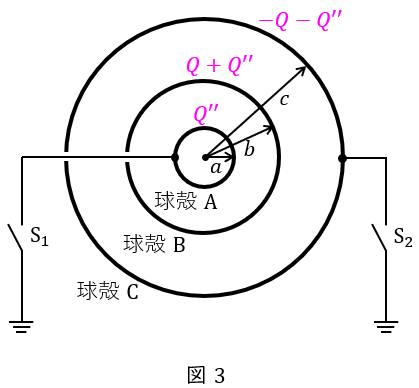
(2)と同様に,\( \ \mathrm {S_{1}} \ \)と\( \ \mathrm {S_{2}} \ \)を共に閉じているときの,球殻\( \ \mathrm {A} \ \)の電荷を\( \ Q^{\prime \prime } \ \)とすると,図3に示すように球殻\( \ \mathrm {C} \ \)が接地されているため,球殻\( \ \mathrm {C} \ \)に蓄えられる電荷は\( \ -Q-Q^{\prime \prime } \ \)となる。
このとき(2)と同様に,球殻\( \ \mathrm {B} \ \)の内外の電界\( \ E_{\mathrm {r1}}^{\prime } \ \)及び\( \ E_{\mathrm {r2}}^{\prime } \ \)は,ワンポイント解説「1.ガウスの法則」の通り,
\[
\begin{eqnarray}
E_{\mathrm {r1}}^{\prime } &=& \frac {Q^{\prime \prime }}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ]
E_{\mathrm {r2}}^{\prime } &=& \frac {Q+Q^{\prime \prime }}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となり,球殻\( \ \mathrm {C} \ \)を基準とした球殻\( \ \mathrm {A} \ \)の電位\( \ V_{\mathrm {A}}^{\prime \prime } \ \)は,ワンポイント解説「2.空間上の電位\( \ V \ \)」の通り,
\[
\begin{eqnarray}
V_{\mathrm {A}}^{\prime \prime }&=&-\int _{b}^{a}E_{\mathrm {r1}}^{\prime }\mathrm {d}r-\int _{c}^{b}E_{\mathrm {r2}}^{\prime }\mathrm {d}r \\[ 5pt ]
&=&-\int _{b}^{a}\frac {Q^{\prime \prime }}{4\pi \varepsilon _{0}r^{2}}\mathrm {d}r-\int _{c}^{b}\frac {Q+Q^{\prime \prime }}{4\pi \varepsilon _{0}r^{2}}\mathrm {d}r \\[ 5pt ]
&=&-\frac {Q^{\prime \prime }}{4\pi \varepsilon _{0}}\int _{b}^{a}\frac {1}{r^{2}}\mathrm {d}r-\frac {Q+Q^{\prime \prime }}{4\pi \varepsilon _{0}}\int _{c}^{b}\frac {1}{r^{2}}\mathrm {d}r \\[ 5pt ]
&=&-\frac {Q^{\prime \prime }}{4\pi \varepsilon _{0}}\left[ -\frac {1}{r}\right] _{b}^{a}-\frac {Q+Q^{\prime \prime }}{4\pi \varepsilon _{0}}\left[ -\frac {1}{r}\right] _{c}^{b} \\[ 5pt ]
&=&-\frac {Q^{\prime \prime }}{4\pi \varepsilon _{0}}\left( -\frac {1}{a}+\frac {1}{b}\right) -\frac {Q+Q^{\prime \prime }}{4\pi \varepsilon _{0}}\left( -\frac {1}{b}+\frac {1}{c}\right) \\[ 5pt ]
&=&-\frac {1}{4\pi \varepsilon _{0}}\left( -\frac {Q^{\prime \prime }}{a}+\frac {Q^{\prime \prime }}{b}-\frac {Q+Q^{\prime \prime }}{b}+\frac {Q+Q^{\prime \prime }}{c}\right) \\[ 5pt ]
&=&-\frac {1}{4\pi \varepsilon _{0}}\left( -\frac {Q^{\prime \prime }}{a}-\frac {Q}{b}+\frac {Q+Q^{\prime \prime }}{c}\right) \\[ 5pt ]
&=&\frac {1}{4\pi \varepsilon _{0}}\left( \frac {Q^{\prime \prime }}{a}+\frac {Q}{b}-\frac {Q+Q^{\prime \prime }}{c}\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,球殻\( \ \mathrm {A} \ \)は接地されているので,\( \ V_{\mathrm {A}}^{\prime }=0 \ \)であるから,
\[
\begin{eqnarray}
\frac {1}{4\pi \varepsilon _{0}}\left( \frac {Q^{\prime \prime }}{a}+\frac {Q}{b}-\frac {Q+Q^{\prime \prime }}{c}\right) &=&0 \\[ 5pt ]
\frac {Q^{\prime \prime }}{a}+\frac {Q}{b}-\frac {Q+Q^{\prime \prime }}{c}&=&0 \\[ 5pt ]
\frac {Q^{\prime \prime }}{a}-\frac {Q^{\prime \prime }}{c} &=&\frac {Q}{c}-\frac {Q}{b} \\[ 5pt ]
\frac {c-a}{ac}Q^{\prime \prime } &=&\frac {b-c}{bc}Q \\[ 5pt ]
Q^{\prime \prime } &=&\frac {b-c}{bc}Q\times \frac {ac}{c-a} \\[ 5pt ]
&=&\frac {\left( b-c\right) a}{\left( c-a\right) b}Q \\[ 5pt ]
\end{eqnarray}
\]
となり,球殻\( \ \mathrm {C} \ \)には\( \ -Q-Q^{\prime \prime } \ \)の電荷が蓄えられるので,
\[
\begin{eqnarray}
-Q-Q^{\prime \prime } &=&-Q-\frac {\left( b-c\right) a}{\left( c-a\right) b}Q \\[ 5pt ]
&=&\frac {-\left( c-a\right) b-\left( b-c\right) a}{\left( c-a\right) b}Q \\[ 5pt ]
&=&\frac {-bc+ab-ab+ac}{\left( c-a\right) b}Q \\[ 5pt ]
&=&\frac {-bc+ac}{\left( c-a\right) b}Q \\[ 5pt ]
&=&\frac {\left( a-b\right) c}{\left( c-a\right) b}Q \\[ 5pt ]
&=&-\frac {\left( b-a\right) c}{\left( c-a\right) b}Q \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん