【問題】
【難易度】★★★★★(難しい)
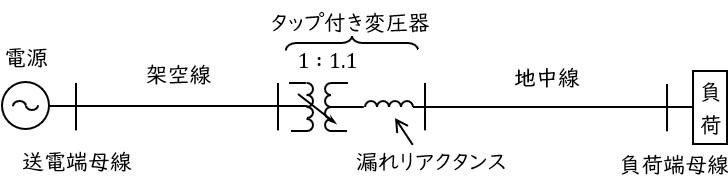
図のような電源,架空線,変圧器,地中線及び負荷で構成される電力系統を考える。架空線の公称電圧は\( \ 500 \ \mathrm {[kV]} \ \),架空線の長さは\( \ 100 \ \mathrm {[km]} \ \)とする。変圧器はその容量を\( \ 1 \ 000 \ \mathrm {[MV\cdot A]} \ \),漏れリアクタンスを自己容量ベースで\( \ 15 \ \mathrm {[%]} \ \)とし,タップ比は図のように\( \ 1 : 1.1 \ \)とする。地中線の公称電圧は\( \ 275 \ \mathrm {[kV]} \ \),地中線の長さは\( \ 50 \ \mathrm {[km]} \ \)とする。架空線,変圧器,地中線とも直列レジスタンス及び分路コンダクタンスは無視する。なお,単位法の系統基準容量を\( \ 1 \ 000 \ \mathrm {[MV\cdot A]} \ \)とし,基準電圧は架空線,地中線ともそれぞれの公称電圧とする。数値はすべて単位法\( \ \mathrm {[p.u.]} \ \)で表すものとする。また,架空線のリアクタンスは\( \ j0.001 \ \mathrm {[p.u. / km]} \ \)で静電容量による分路サセプタンスは\( \ j0.001 \ \mathrm {[p.u. / km]} \ \)とし,地中線のリアクタンスは\( \ j0.002 \ \mathrm {[p.u. / km]} \ \)で静電容量による分路サセプタンスは\( \ j0.008 \ \mathrm {[p.u. / km]} \ \)とする。この送電系統で,架空線送電端電圧を\( \ 525 \ \mathrm {[kV]} \ \)としたとき,次の問に答えよ。
(1) 架空線,変圧器,地中線を\( \ \pi \ \)形等価回路で表現し,それらを接続した送電系統全体の等価回路を表せ。なお,それぞれの直列リアクタンス,分路サセプタンスは単位法で表すものとする。
(2) この送電系統の負荷端の短絡電流を表すアドミタンスと,無負荷時の負荷端電圧をそれぞれ単位法で計算せよ。ただし,電源の内部インピーダンスは無視する。
(3) 負荷として\( \ 1.0+j0.8 \ \mathrm {[p.u.]} \ \)のインピーダンスを接続したとき,負荷端の電圧\( \ \mathrm {[p.u.]} \ \)を求めよ。また,軽負荷時に負荷のインピーダンスが\( \ 4.0+j3.2 \ \mathrm {[p.u.]} \ \)まで上昇し,変圧器のタップ比をそのままとしたときの,負荷端の電圧\( \ \mathrm {[p.u.]} \ \)を計算せよ。
【ワンポイント解説】
\( \ \pi \ \)形等価回路を利用した計算問題です。
変圧器の\( \ \pi \ \)形等価回路の知識が問われており,さらに計算量も多いため,受験生を大変悩ませた問題かと思います。
問3とともに選択しない能力も問われていると思って下さい。
1.オーム法から単位法への変換
基準容量\( \ P_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ \),基準電圧\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \),基準電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)の時,インピーダンス\( \ Z \ \mathrm {[\Omega ]} \ \)を単位法で表すと,
\[
\begin{eqnarray}
Z \ \mathrm {[p.u.]} \ &=&\frac {Z \ [\Omega ] \ I_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}} (定義) \\[ 5pt ]
&=&\frac {\sqrt {3}Z \ [\Omega ] \ I_{\mathrm {n}}}{V_{\mathrm {n}}} \\[ 5pt ]
&=&\frac {\sqrt {3}Z \ [\Omega ] \ V_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}} \\[ 5pt ]
&=&\frac {P_{\mathrm {n}}Z \ [\Omega ] \ }{V_{\mathrm {n}}^{2}} (∵P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ]
\end{eqnarray}
\]
となります。
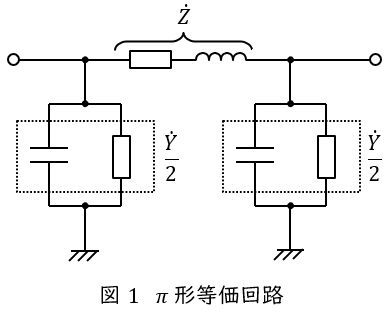
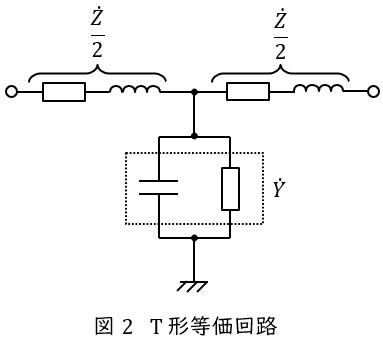
2.\( \ \pi \ \)形等価回路と\( \ \mathrm {T} \ \)形等価回路
送電線のこう長が大きくなると送電線のリアクタンスや静電容量が無視できなくなるので,\( \ \pi \ \)形等価回路や\( \ \mathrm {T} \ \)形等価回路を適用します。送電線のインピーダンスを\( \ \dot Z \ \),アドミタンスを\( \ \dot Y \ \)とすると,\( \ \pi \ \)形等価回路は図1,\( \ \mathrm {T} \ \)形等価回路は図2のようになります。
電験では送電線の抵抗分やサセプタンス分は無視し,送電線のインダクタンスを\( \ L \ \mathrm {[H]} \ \),静電容量を\( \ C \ \mathrm {[F]} \ \)として,
\[
\begin{eqnarray}
{\dot Z}&=&\mathrm {j}\omega L \\[ 5pt ]
{\dot Y}&=&\mathrm {j}\omega C \\[ 5pt ]
\end{eqnarray}
\]
として扱う問題がほとんどです。
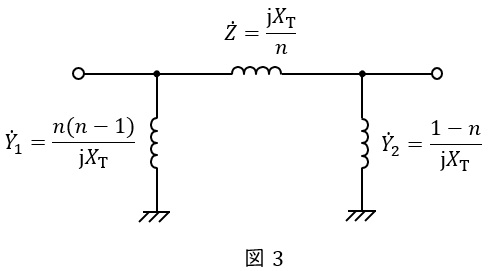
3.変圧器の\( \ \pi \ \)形等価回路
タップ比が\( \ 1:n \ \),漏れリアクタンスが\( \ X_{\mathrm {T}} \ \)の変圧器の\( \ \pi \ \)形等価回路は図3のようになります。送電線と比べ各係数が複雑になります。各インピーダンスとアドミタンスの係数は四端子定数の考え方を用いて導出することは可能ですが,電験対策としては基本的には覚えるしかない内容かと思います。
【解答】
(1)架空線,変圧器,地中線の\( \ \pi \ \)形等価回路とそれらを接続した送電系統全体の等価回路
架空線のリアクタンス\( \ \dot Z_{oL} \ \mathrm {[p.u.]} \ \)及び分路サセプタンス\( \ \dot Y_{oC} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
\dot Z_{oL}&=&j0.001\times 100 \\[ 5pt ]
&=&j0.1 \ \mathrm {[p.u.]} \\[ 5pt ]
\dot Y_{oC}&=&j0.001\times 100 \\[ 5pt ]
&=&j0.1 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,ワンポイント解説「2.\( \ \pi \ \)形等価回路と\( \ \mathrm {T} \ \)形等価回路」の通り,\( \ \pi \ \)形等価回路は図4のようになる。
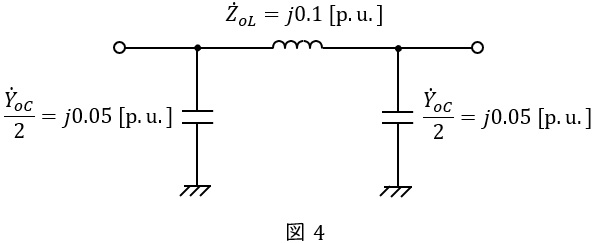
変圧器のリアクタンス\( \ X_{T}=0.15 \ \mathrm {[p.u.]} \ \)であるので,\( \ \pi \ \)形等価回路のインピーダンス\( \ \dot Z _{T} \ \mathrm {[p.u.]} \ \)及びアドミタンス\( \ \dot Y _{1T} \ \mathrm {[p.u.]} \ \),\( \ \dot Y _{2T} \ \mathrm {[p.u.]} \ \)は,ワンポイント解説「3.変圧器の\( \ \pi \ \)形等価回路」の通り,
\[
\begin{eqnarray}
\dot Z _{T}&=&\frac {jX_{T}}{n} \\[ 5pt ]
&=&\frac {j0.15}{1.1} \\[ 5pt ]
&≒&j0.136 \ 36 \ \mathrm {[p.u.]} \\[ 5pt ]
\dot Y _{1T}&=&\frac {n\left( n-1\right) }{jX_{T}} \\[ 5pt ]
&=&\frac {1.1\times \left( 1.1-1\right) }{j0.15} \\[ 5pt ]
&≒&-j0.733 \ 33 \ \mathrm {[p.u.]} \\[ 5pt ]
\dot Y _{2T}&=&\frac {1-n}{jX_{T}} \\[ 5pt ]
&=&\frac {1-1.1}{j0.15} \\[ 5pt ]
&≒&j0.666 \ 67 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ \pi \ \)形等価回路は図5のようになる。
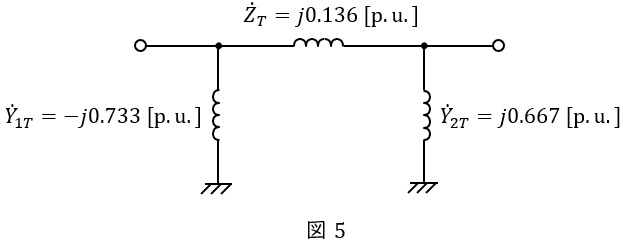
地中線のリアクタンス\( \ \dot Z_{uL} \ \mathrm {[p.u.]} \ \)及び分路サセプタンス\( \ \dot Y_{uC} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
\dot Z_{uL}&=&j0.002\times 50 \\[ 5pt ]
&=&j0.1 \ \mathrm {[p.u.]} \\[ 5pt ]
\dot Y_{uC}&=&j0.008\times 50 \\[ 5pt ]
&=&j0.4 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,ワンポイント解説「2.\( \ \pi \ \)形等価回路と\( \ \mathrm {T} \ \)形等価回路」の通り,\( \ \pi \ \)形等価回路は図6のようになる。
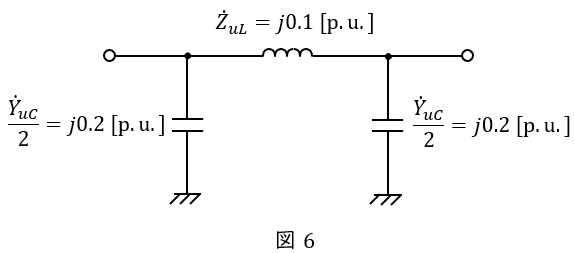
架空線のサセプタンス\( \ \displaystyle \frac {\dot Y_{oC}}{2} \ \mathrm {[p.u.]} \ \)と変圧器のアドミタンス\( \ \dot Y _{1T} \ \mathrm {[p.u.]} \ \)の合成アドミタンス\( \ \dot Y _{1} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
\dot Y _{1}&=&\frac {\dot Y_{oC}}{2}+\dot Y _{1T} \\[ 5pt ]
&=&\frac {j0.1}{2}-j0.733 \ 33 \\[ 5pt ]
&=&-j0.683 \ 33 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
であり,変圧器のアドミタンス\( \ \dot Y _{2T} \ \mathrm {[p.u.]} \ \)と地中線のサセプタンス\( \ \displaystyle \frac {\dot Y_{uC}}{2} \ \mathrm {[p.u.]} \ \)の合成アドミタンス\( \ \dot Y _{2} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
\dot Y _{2}&=&\dot Y _{2T}+\frac {\dot Y_{uC}}{2} \\[ 5pt ]
&=&j0.666 \ 67+\frac {j0.4}{2} \\[ 5pt ]
&=&j0.866 \ 67 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,送電系統全体の等価回路は図7のようになる。
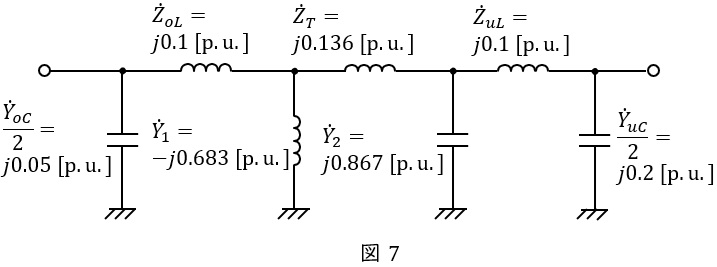
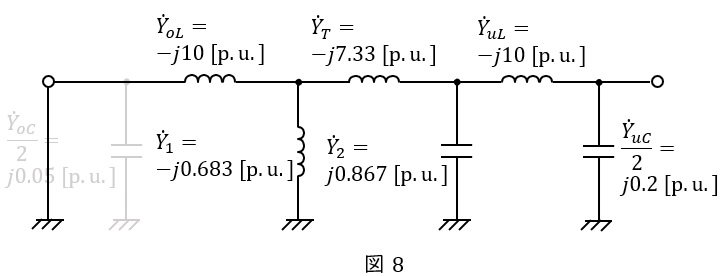
(2)負荷端の短絡電流を表すアドミタンスと無負荷時の負荷端電圧を単位法で計算
架空線のリアクタンスの逆数\( \ \displaystyle \dot Y_{oL}=\frac {1}{\dot Z_{oL}} \ \mathrm {[p.u.]} \ \),変圧器のインピーダンスの逆数\( \ \displaystyle \dot Y_{T}=\frac {1}{\dot Z_{T}} \ \mathrm {[p.u.]} \ \),地中線のリアクタンス\( \ \displaystyle \dot Y_{uL}=\frac {1}{\dot Z_{uL}} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
\dot Y_{oL}&=&\frac {1}{\dot Z_{oL}} \\[ 5pt ]
&=&\frac {1}{j0.1} \\[ 5pt ]
&=&-j10 \ \mathrm {[p.u.]} \\[ 5pt ]
\dot Y_{T}&=&\frac {1}{\dot Z_{T}} \\[ 5pt ]
&=&\frac {1}{j0.136 \ 36} \\[ 5pt ]
&≒&-j7.333 \ 5 \ \mathrm {[p.u.]} \\[ 5pt ]
\dot Y_{uL}&=&\frac {1}{\dot Z_{uL}} \\[ 5pt ]
&=&\frac {1}{j0.1} \\[ 5pt ]
&=&-j10 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,負荷端からみたアドミタンスは図8のようになる。図8から合成アドミタンスを順に求めていくと,\( \ \dot Y_{oL} \ \),\( \ \dot Y_{1} \ \),\( \ \dot Y_{T} \ \)の合成アドミタンス\( \ \dot Y_{s1} \ \)は,
\[
\begin{eqnarray}
\dot Y_{s1}&=&\frac {\left( \dot Y_{oL}+\dot Y_{1}\right) \dot Y_{T}}{\left( \dot Y_{oL}+\dot Y_{1}\right) +\dot Y_{T}} \\[ 5pt ]
&=&\frac {\left( -j10-j0.683 \ 33\right) \left( -j7.333 \ 5\right) }{\left( -j10-j0.683 \ 33\right) -j7.333 \ 5} \\[ 5pt ]
&=&-j4.348 \ 5 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となり,回路全体のアドミタンス\( \ \dot Y_{s} \ \)は,
\[
\begin{eqnarray}
\dot Y_{s}&=&\frac {\left( \dot Y_{s1}+\dot Y_{2}\right) \dot Y_{uL}}{\left( \dot Y_{s1}+\dot Y_{2}\right) +\dot Y_{uL}}+\frac {\dot Y_{uC}}{2} \\[ 5pt ]
&=&\frac {\left( -j4.348 \ 5+j0.866 \ 67\right) \left( -j10\right) }{\left( -j4.348 \ 5+j0.866 \ 67\right) -j10}+\frac {j0.4}{2} \\[ 5pt ]
&=&-j2.382 \ 6 → -j2.38 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
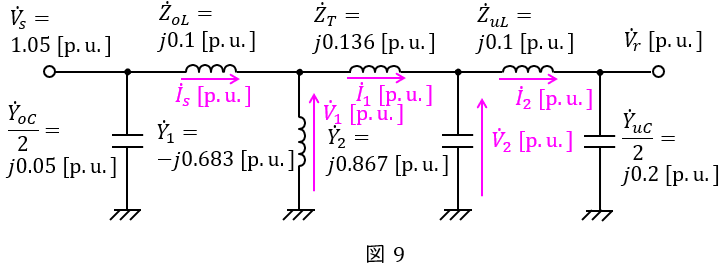
無負荷時の負荷端電圧を\( \ {\dot V}_{r} \ \mathrm {[p.u.]} \ \)とする。送電端電圧\( \ {\dot V}_{s} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
{\dot V}_{s}&=&\frac {525}{500} \\[ 5pt ]
&=&1.05 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となり,図に示すと図9のようになる。ただし,各電圧,電流を図のようにおく。図9より,
\[
\begin{eqnarray}
{\dot I}_{2}&=&\frac {\dot Y_{uC}}{2}{\dot V}_{r} \\[ 5pt ]
&=&\frac {j0.4}{2}{\dot V}_{r} \\[ 5pt ]
&=&j0.2{\dot V}_{r} \\[ 5pt ]
{\dot V}_{2}&=&{\dot V}_{r}+\dot Z_{uL}{\dot I}_{2} \\[ 5pt ]
&=&{\dot V}_{r}+j0.1\cdot j0.2{\dot V}_{r} \\[ 5pt ]
&=&0.98{\dot V}_{r} \\[ 5pt ]
{\dot I}_{1}&=&{\dot I}_{2}+\dot Y_{2}{\dot V}_{2} \\[ 5pt ]
&=&j0.2{\dot V}_{r}+j0.866 \ 7 \cdot 0.98{\dot V}_{r} \\[ 5pt ]
&≒&j1.049 \ 3{\dot V}_{r} \\[ 5pt ]
{\dot V}_{1}&=&{\dot V}_{2}+\dot Z_{T}{\dot I}_{1} \\[ 5pt ]
&=&0.98{\dot V}_{r}+j0.136 \ 36\cdot j1.049 \ 3{\dot V}_{r} \\[ 5pt ]
&≒&0.836 \ 92{\dot V}_{r} \\[ 5pt ]
{\dot I}_{s}&=&{\dot I}_{1}+\dot Y_{1}{\dot V}_{1} \\[ 5pt ]
&=&j1.049 \ 3{\dot V}_{r}-j0.683 \ 33 \cdot 0.836 \ 92{\dot V}_{r} \\[ 5pt ]
&≒&j0.477 \ 41{\dot V}_{r} \\[ 5pt ]
{\dot V}_{s}&=&{\dot V}_{1}+\dot Z_{oL}{\dot I}_{s} \\[ 5pt ]
&=&0.836 \ 92{\dot V}_{r}+j0.1\cdot j0.477 \ 41{\dot V}_{r} \\[ 5pt ]
&≒&0.789 \ 18{\dot V}_{r} \\[ 5pt ]
\end{eqnarray}
\]
の関係があるので,\( \ {\dot V}_{r} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
{\dot V}_{r}&=&\frac {{\dot V}_{s}}{0.789 \ 18} \\[ 5pt ]
&=&\frac {1.05}{0.789 \ 18} \\[ 5pt ]
&≒&1.33 \ 05 → 1.33 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
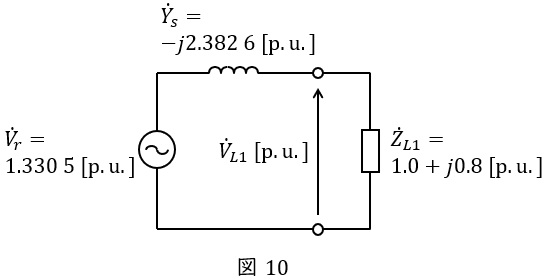
(3)負荷として\( \ 1.0+j0.8 \ \mathrm {[p.u.]} \ \)を接続したときの負荷端の電圧\( \ \mathrm {[p.u.]} \ \),軽負荷時に負荷のインピーダンスが\( \ 4.0+j3.2 \ \mathrm {[p.u.]} \ \)まで上昇したときの負荷端の電圧\( \ \mathrm {[p.u.]} \ \)
鳳・テブナンの定理より,負荷\( \ {\dot Z}_{L1}=1.0+j0.8 \ \mathrm {[p.u.]} \ \)を接続したときの回路は図10のようになる。このときの負荷端の電圧の大きさ\( \ V_{L1} \ \mathrm {[p.u.]} \ \)は,分圧の法則より,
\[
\begin{eqnarray}
V_{L1}&=&\left| \frac {\dot Z_{L1}}{\displaystyle \frac {1}{\dot Y_{s}}+\dot Z_{L1}}\dot V_{r}\right| \\[ 5pt ]
&=&\left| \frac {1.0+j0.8}{\displaystyle \frac {1}{-j2.382 \ 6}+1.0+j0.8 }\times 1.33 \ 05 \right| \\[ 5pt ]
&≒&\left| \frac {1.0+j0.8}{j0.419 \ 71+1.0+j0.8 }\times 1.33 \ 05 \right| \\[ 5pt ]
&≒&\left| \frac {1.0+j0.8}{1.0+j1.219 \ 7 }\times 1.33 \ 05 \right| \\[ 5pt ]
&≒& \frac {\sqrt {1.0^{2}+0.8^{2}}}{\sqrt {1.0^{2}+1.219 \ 7 ^{2}}}\times 1.33 \ 05 \\[ 5pt ]
&≒& \sqrt {\frac {1.64}{2.487 \ 7}}\times 1.33 \ 05 \\[ 5pt ]
&≒&1.08 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
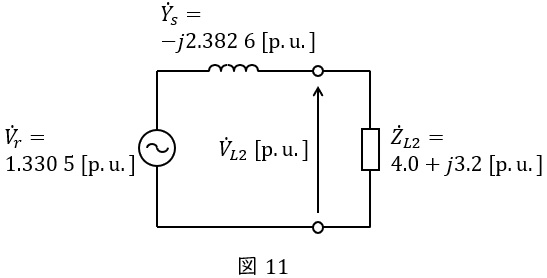
同様に,鳳・テブナンの定理より,負荷\( \ {\dot Z}_{L2}=4.0+j3.2 \ \mathrm {[p.u.]} \ \)を接続したときの回路は図11のようになる。このときの負荷端の電圧の大きさ\( \ V_{L2} \ \mathrm {[p.u.]} \ \)は,分圧の法則より,
\[
\begin{eqnarray}
V_{L2}&=&\left| \frac {\dot Z_{L2}}{\displaystyle \frac {1}{\dot Y_{s}}+\dot Z_{L2}}\dot V_{r}\right| \\[ 5pt ]
&=&\left| \frac {4.0+j3.2}{\displaystyle \frac {1}{-j2.382 \ 6}+4.0+j3.2 }\times 1.33 \ 05 \right| \\[ 5pt ]
&≒&\left| \frac {4.0+j3.2}{j0.419 \ 71+4.0+j3.2 }\times 1.33 \ 05 \right| \\[ 5pt ]
&≒&\left| \frac {4.0+j3.2}{4.0+j3.619 \ 7 }\times 1.33 \ 05 \right| \\[ 5pt ]
&≒& \frac {\sqrt {4.0^{2}+3.2^{2}}}{\sqrt {4.0^{2}+3.619 \ 7 ^{2}}}\times 1.33 \ 05 \\[ 5pt ]
&≒& \sqrt {\frac {26.24}{29.102}}\times 1.33 \ 05 \\[ 5pt ]
&≒&1.26 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん