《理論》〈電子理論〉[H19:問7]2段縦続接続したトランジスタ増幅回路の電圧増幅度に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，トランジスタ増幅回路に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる数値を記述用紙の解答欄に記入しなさい。ただし，答に小数点以下が生じた場合，小数点以下を四捨五入して整数値として表しなさい。また，数値は絶対値ではなく，符号も含めて解答しなさい。

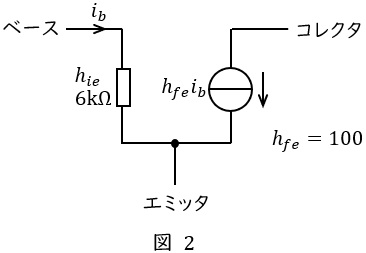
図1のトランジスタ増幅回路において，$ \ v_{in} \ $は入力交流信号電圧，$ \ v_{o1} \ $は出力交流信号電圧である。ただし，すべてのコンデンサは交流信号周波数において短絡と見なせ，トランジスタの交流等価回路は図2で表されるとする。

図1において，$ \ \mathrm {A-A^{\prime }} \ $より右をみた回路の入力抵抗は$ \ R_{in}= \ \fbox {　（１）　} \ \mathrm {[k\Omega ]} \ $である。また，電圧増幅度は$ \ \displaystyle \frac {v_{o1}}{v_{in}}= \ \fbox {　（２）　} \ $倍である。

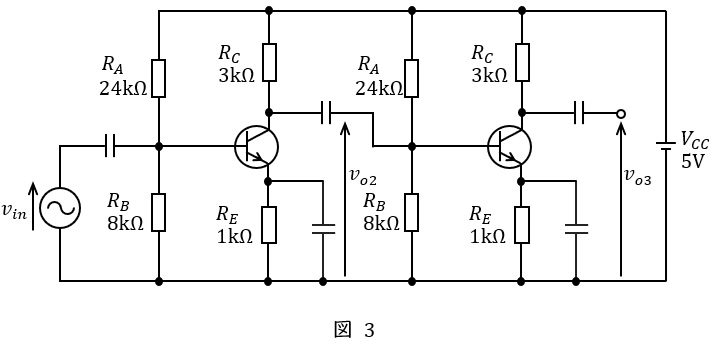
次に，図1の回路を図3のように$ \ 2 \ $段縦続接続した。ただし，$ \ v_{o2} \ $，$ \ v_{o3} \ $はそれぞれ$ \ 1 \ $段目，$ \ 2 \ $段目の交流出力信号電圧である。このとき，$ \ 1 \ $段目の電圧増幅度は$ \ \displaystyle \frac {v_{o2}}{v_{in}}= \ \fbox {　（３）　} \ $倍となり，また，$ \ 2 \ $段目の電圧増幅度は$ \ \displaystyle \frac {v_{o3}}{v_{o2}}= \ \fbox {　（４）　} \ $倍である。したがって，図3の回路全体の電圧増幅度は$ \ \displaystyle \frac {v_{o3}}{v_{in}}= \ \fbox {　（５）　} \ $倍となる。

【ワンポイント解説】

エミッタ接地トランジスタ増幅回路を$ \ 2 \ $段接続した回路の電圧増幅度を考える問題で，(3)の考え方がわかると高得点が得られる問題です。
小信号等価回路は原則与えられる回路ですが，本問の場合は与えられませんでした。覚えていない方は小信号等価回路がどのようになるかよく考えて導き出すようにして下さい。

1.エミッタ接地回路の小信号等価回路
図4に示すようなエミッタ接地トランジスタ増幅回路において，信号成分（交流）（入力$ \ v_{\mathrm {i}} \ $及び出力$ \ v_{\mathrm {o}} \ $）のみを考える場合，直流成分$ \ V_{\mathrm {CC}} \ $を零としたときの回路となり，コンデンサは短絡として扱います。これにより，$ \ R_{\mathrm {1}} \ $と$ \ R_{\mathrm {2}} \ $が並列となり，$ \ v_{\mathrm {o}} \ $が$ \ R_{\mathrm {C}} \ $に加わる電圧となります。したがって，小信号等価回路は図5のようになります。

【解答】

(1)解答：$ \ 3 \ $
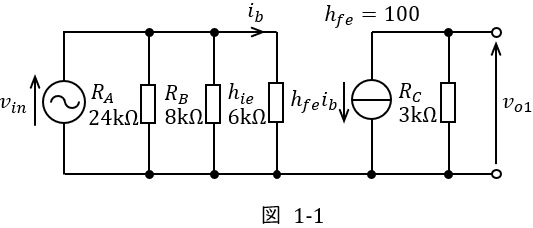
ワンポイント解説「1.エミッタ接地回路の小信号等価回路」の通り，図1の小信号等価回路は図1-1のようになる。
図1-1より，$ \ \mathrm {A-A^{\prime }} \ $より右をみた回路の入力抵抗$ \ R_{in} \ \mathrm {[k\Omega ]} \ $は，
\[
\begin{eqnarray}
\frac {1}{R_{in}} &=&\frac {1}{R_{A}}+\frac {1}{R_{B}}+\frac {1}{h_{ie}} \\[ 5pt ] &=&\frac {1}{24}+\frac {1}{8}+\frac {1}{6} \\[ 5pt ] &=&\frac {1+3+4}{24} \\[ 5pt ] &=&\frac {1}{3} \\[ 5pt ] R_{in}&=&3 \ \mathrm {[k\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：$ \ -50 \ $
図1-1より，
\[
\begin{eqnarray}
v_{in}&=&h_{ie}i_{b} \\[ 5pt ] v_{o1}&=&-R_{C}h_{fe}i_{b} \\[ 5pt ] \end{eqnarray}
\] であるから，電圧増幅度$ \ \displaystyle \frac {v_{o1}}{v_{in}} \ $は，
\[
\begin{eqnarray}
\frac {v_{o1}}{v_{in}}&=&\frac {-R_{C}h_{fe}i_{b}}{h_{ie}i_{b}} \\[ 5pt ] &=&-\frac {R_{C}h_{fe}}{h_{ie}} \\[ 5pt ] &=&-\frac {3\times 100}{6} \\[ 5pt ] &=&-50 \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：$ \ -25 \ $
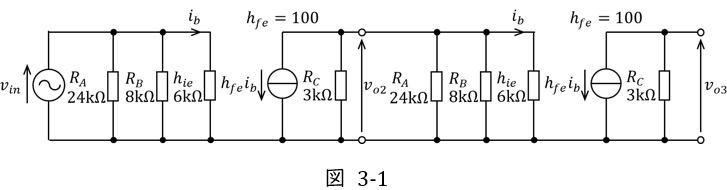
図3の小信号等価回路は図3-1のようになる。
図3において，中間段の$ \ R_{C}=3 \ \mathrm {[k\Omega ]} \ $，$ \ R_{A}=24 \ \mathrm {[k\Omega ]} \ $，$ \ R_{B}=8 \ \mathrm {[k\Omega ]} \ $，$ \ h_{ie}=6 \ \mathrm {[k\Omega ]} \ $の合成抵抗$ \ R_{M} \ \mathrm {[k\Omega ]} \ $は，
\[
\begin{eqnarray}
\frac {1}{R_{M}} &=&\frac {1}{R_{C}}+\frac {1}{R_{A}}+\frac {1}{R_{B}}+\frac {1}{h_{ie}} \\[ 5pt ] &=&\frac {1}{3}+\frac {1}{3} \\[ 5pt ] &=&\frac {2}{3} \\[ 5pt ] R_{M}&=&1.5 \ \mathrm {[k\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となり，
\[
\begin{eqnarray}
v_{in}&=&h_{ie}i_{b} \\[ 5pt ] v_{o2}&=&-R_{M}h_{fe}i_{b} \\[ 5pt ] \end{eqnarray}
\] であるから，電圧増幅度$ \ \displaystyle \frac {v_{o2}}{v_{in}} \ $は，
\[
\begin{eqnarray}
\frac {v_{o2}}{v_{in}}&=&\frac {-R_{M}h_{fe}i_{b}}{h_{ie}i_{b}} \\[ 5pt ] &=&-\frac {R_{M}h_{fe}}{h_{ie}} \\[ 5pt ] &=&-\frac {1.5\times 100}{6} \\[ 5pt ] &=&-25 \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：$ \ -50 \ $
$ \ 2 \ $段目の電圧増幅度は(2)の条件と同じであるから，$ \ -50 \ $倍と求められる。

(5)解答：$ \ 1 \ 250 \ $
(3)及び(4)より，電圧増幅度$ \ \displaystyle \frac {v_{o3}}{v_{in}} \ $は，
\[
\begin{eqnarray}
\frac {v_{o3}}{v_{in}}&=&\frac {v_{o3}}{v_{o2}}\cdot \frac {v_{o2}}{v_{in}} \\[ 5pt ] &=&-50\times \left( -25\right) \\[ 5pt ] &=&1 \ 250 \\[ 5pt ] \end{eqnarray}
\] と求められる。