《理論》〈電磁気〉[H26:問2] 導体及び抵抗体周辺における電界・磁界に関する空欄穴埋問題

【問題】

【難易度】★★★☆☆（普通）

次の文章は，導体及び抵抗体周辺における電界・磁界に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選びなさい。

導体\( \ \mathrm {A} \ \)と導体\( \ \mathrm {B} \ \)の間に円柱状の抵抗体が挿入されており，導体\( \ \mathrm {A} \ \)から導体\( \ \mathrm {B} \ \)に向けて直流電流\( \ I \ \)が一様に流れている図1のような状態を考える。ここで，導体\( \ \mathrm {A} \ \)の電位\( \ V_{\mathrm {A}} \ \)と導体\( \ \mathrm {B} \ \)の電位\( \ V_{\mathrm {B}} \ \)は\( \ V_{\mathrm {A}}＞V_{\mathrm {B}}＞0 \ \)とし，導体\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)での電圧降下は零とする。

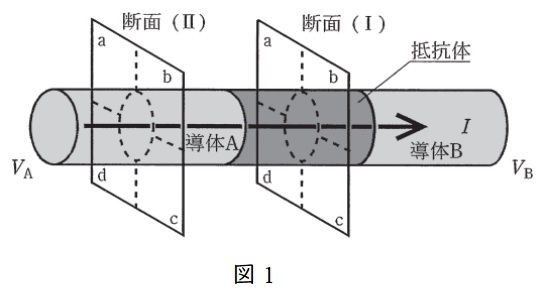
このとき，図中の断面(Ⅰ)において，断面と垂直な方向の電界成分を模式的に描いたものとしてふさわしいのは\( \ \fbox {　 （１） 　} \ \)である。また，断面と平行な方向の磁界成分を磁力線を用いて模式的に描いたものとしてふさわしいのは\( \ \fbox {　 （２） 　} \ \)である。

ポインティングベクトル\( \ \vec {S} \ \)は電界\( \ \vec {E} \ \)及び磁界\( \ \vec {H} \ \)を用いて\( \ \vec {S}=\vec {E}\times \vec {H} \ \)と表されるため，断面(Ⅰ)における断面と平行な方向のポインティングベクトルの様子を模式的に描くと，\( \ \fbox {　 （３） 　} \ \)のようになる。

次に，断面(Ⅱ)における断面と平行な方向の電界成分を電気力線を用いて模式的に描いたものとしてふさわしいのは\( \ \fbox {　 （４） 　} \ \)である。断面と平行な方向の磁界成分を磁力線を用いて模式的に描いたものとしてふさわしいのは\( \ \fbox {　 （２） 　} \ \)なので，断面と垂直な方向のポインティングベクトルの様子を模式的に描くと\( \ \fbox {　 （５） 　} \ \)のようになる。

このように，ポインティングベクトルを用いてエネルギーの流れを考察すると，抵抗体周辺の空間から抵抗体に向けてエネルギーの一部が流入していることがわかる。

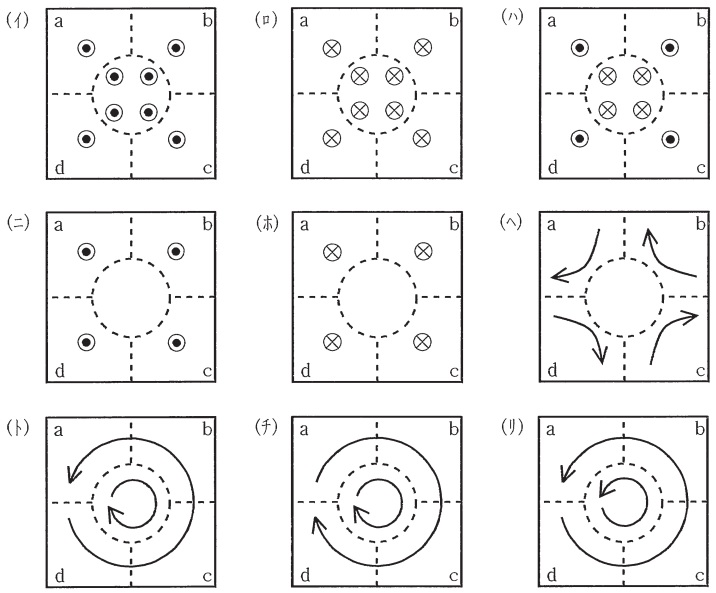
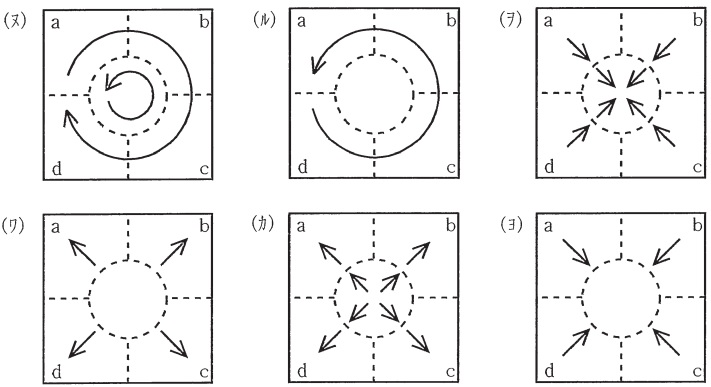
なお，解答群(イ)～(ヨ)の図において，\( \ \otimes \ \)は図1において左から右に断面を横切る向きを，\( \ \odot \ \)は図1において右から左に断面を横切る向きを示す。また，円の内部に何も記していないものは，その成分が導体内あるいは抵抗体内で零であることを意味している。導体\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)は十分長いものとし，電位\( \ V_{\mathrm {A}} \ \)，\( \ V_{\mathrm {B}} \ \)の基準としては，導体\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)の同軸で半径が十分大きい円筒の電位を零とする。

〔問2の解答群〕

【ワンポイント解説】

ポインティングベクトルは電界\( \ \vec {E} \ \)及び磁界\( \ \vec {H} \ \)の外積で定義される物理量で，電磁エネルギーの流れの向きとなります。電磁気には珍しく，計算の全くない問題となっています。

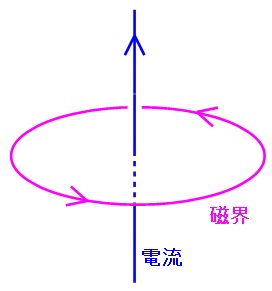
1.右ねじの法則
電流の向きを右ねじの進む向きとすると，磁界がねじを回す向きになるという法則です。

2.ポインティングベクトル
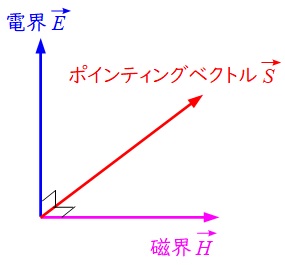
ポインティングベクトルは電界\( \ \vec {E} \ \)及び磁界\( \ \vec {H} \ \)の外積で定義される物理量で，電磁エネルギーの流れの向きとなり，電界と磁界の向きが与えられているとすると，下図の通り，その両方の成分と直角の向きとなります。電界から磁界に向かって右ねじを回すとき，右ねじが進むがポインティングベクトルの向きとなります。

【解答】

(1)解答：ロ
題意より，図中の断面1において\( \ V_{\mathrm {A}}＞V_{\mathrm {B}}＞0 \ \)であり電流\( \ I \ \)は一様に分布しているので，電界は導体\( \ \mathrm {A} \ \)から導体\( \ \mathrm {B} \ \)に一様に分布することになる。よって，電界成分にふさわしいのは(ロ)となる。

(2)解答：チ
ワンポイント解説「1.右ねじの法則」より，電界の向きに対し，磁界は右回りの分布となる。よって，磁界成分にふさわしいのは(チ)となる。

(3)解答：ヲ
ワンポイント解説「2.ポインティングベクトル」より，ポインティングベクトルは電界から磁界に向かって右ねじを回すとき，右ねじが進む向きであるから，全ての場所において，図の中心部に向かうベクトルとなる。よって，(ヲ)となる。

(4)解答：ワ
断面(Ⅱ)において，導体内の電位は等しく，導体から離れると無限遠に向かって，\( \ V=\frac {Q}{4\pi \varepsilon _{0} r} \ \)の分布で電位が下がっていくので，電界の向きは外向きのベクトルとなる。よって，(ワ)となる。

(5)解答：ホ
ワンポイント解説「2.ポインティングベクトル」より，ポインティングベクトルは電界から磁界に向かって右ねじを回すとき，右ねじが進む向きであるから，導体の外においては導体\( \ \mathrm {A} \ \)から導体\( \ \mathrm {B} \ \)に向かう向きとなる。よって，(ホ)となる。