【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,\( \ \mathrm {MIS} \ \)構造においてのしきい値に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選びなさい。なお,\( \ \varepsilon _{0} \ \)は真空の誘電率,\( \ \varepsilon _{\mathrm {s}} \ \)は半導体の比誘電率,\( \ \varepsilon _{\mathrm {ox}} \ \)は絶縁体の比誘電率とする。
金属-絶縁物-\( \ \mathrm {p} \ \)形半導体からなる\( \ \mathrm {MIS} \ \)構造において,電圧を印加しないときに半導体内のバンドが一直線であるフラットバンド状態になっているとする。そこからゲートに正方向に電圧を加えると,正孔は半導体表面近傍から存在しなくなり空乏層になる。このとき\( \ \mathrm {p} \ \)形半導体のキャリヤ濃度を\( \ N_{\mathrm {A}} \ \),空乏層の厚さを\( \ l_{\mathrm {D}} \ \)とすると,空乏層内の厚さ方向\( \ x \ \)における電位\( \ \mathit {\phi } \ \)の勾配は,絶縁物-半導体の界面を\( \ x=0 \ \)として
\[
\begin{eqnarray}
\frac {\mathrm {d}\mathit {\phi }}{\mathrm {d}x} &=& \frac {qN_{\mathrm {A}}}{\varepsilon _{\mathrm {s}}\varepsilon _{0}}\left( x-l_{\mathrm {D}}\right) \\[ 5pt ]
\end{eqnarray}
\]
で与えられる。\( \ x=l_{\mathrm {D}} \ \)において電位が零として式を解くと\( \ \mathit {\phi } ( x ) = \ \fbox { (1) } \ \)と表され,\( \ x=0 \ \)での電位(表面電位)は\( \ \mathit {\phi }_{\mathrm {S}}= \ \fbox { (2) } \ \)となる。ここで,空乏状態となった領域でのアクセプタによる単位面積当たりの電荷は\( \ Q=-qN_{\mathrm {A}}l_{\mathrm {D}} \ \)であり,この電荷が絶縁物内に電位差を作る。絶縁物層厚を\( \ t_{\mathrm {ox}} \ \)とすると,この電位差は\( \ \fbox { (3) } \ \)である。\( \ \fbox { (2) } \ \)と\( \ \fbox { (3) } \ \)の和がゲート電圧である。
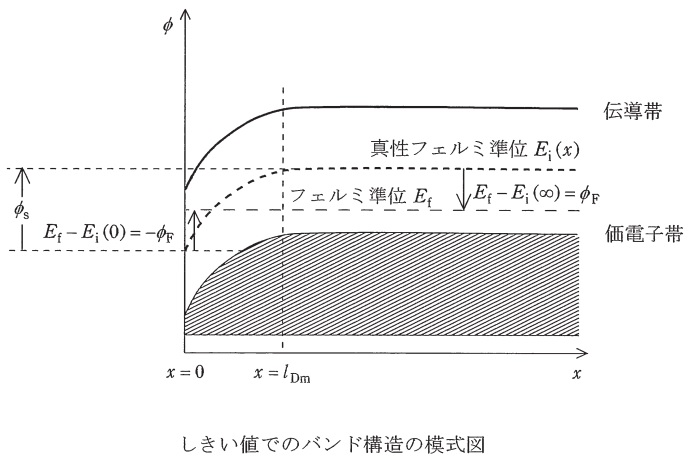
ゲートに印加される電圧が大きくなると,表面電位\( \ \mathit {\phi }_{\mathrm {S}} \ \)も大きくなる。図右側に示す様に\( \ \mathrm {p} \ \)形半導体での平衡状態(\( \ x=\infty \ \) )においてフェルミ準位\( \ E_{\mathrm {f}} \ \)と真性フェルミ準位\( \ E_{\mathrm {i}} ( \infty ) \ \)の差の電位がフェルミポテンシャル\( \ \mathit {\phi }_{\mathrm {F}} \ \)であるが,表面電位\( \ \mathit {\phi }_{\mathrm {S}} \ \)が\( \ 2\mathit {\phi }_{\mathrm {F}} \ \)となった図のようなバンド構造のときに,電子の濃度は半導体の濃度\( \ N_{\mathrm {A}} \ \)と等しくなる。このときのゲート電圧をしきい値と呼ぶ。しきい値よりもゲート電圧が大きくなっても,それに伴い増える電荷は半導体表面の電荷のみであり,空乏層の厚さは変化しない。このしきい値で最大になる空乏層厚さ\( \ l_{\mathrm {Dm}} \ \)は\( \ \fbox { (4) } \ \)である。しきい値は,表面電位に厚さ\( \ l_{\mathrm {Dm}} \ \)の空乏層の電荷が絶縁層に作る電位差を足したものとなり,\( \ \fbox { (5) } \ \)となる。
〔問6の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {Qt_{\mathrm {ox}}}{\varepsilon _{\mathrm {ox}}\varepsilon _{0}} &(ロ)& \sqrt {\frac {\mathit {\phi }_{\mathrm {F}}\varepsilon _{\mathrm {ox}}\varepsilon _{0}}{qN_{\mathrm {A}}}} &(ハ)& \frac {qN_{\mathrm {A}}}{2\varepsilon _{\mathrm {s}}\varepsilon _{0}}\left( x-l_{\mathrm {D}}\right) ^{2} \\[ 5pt ]
&(ニ)& \frac {qN_{\mathrm {A}}}{\varepsilon _{\mathrm {s}}\varepsilon _{0}} x^{2} &(ホ)& 2\mathit {\phi }_{\mathrm {F}}+\frac {qN_{\mathrm {A}}l_{\mathrm {Dm}}t_{\mathrm {ox}}}{\varepsilon _{\mathrm {ox}}\varepsilon _{0}} &(ヘ)& \frac {qN_{\mathrm {A}}}{2\varepsilon _{\mathrm {s}}\varepsilon _{0}}l_{\mathrm {D}} \\[ 5pt ]
&(ト)& \frac {qN_{\mathrm {A}}}{\varepsilon _{\mathrm {s}}\varepsilon _{0}}{l_{\mathrm {D}}}^{2} &(チ)& \frac {qN_{\mathrm {A}}}{2\varepsilon _{\mathrm {s}}\varepsilon _{0}}{l_{\mathrm {D}}}^{2} &(リ)& \frac {Q\varepsilon _{\mathrm {ox}}\varepsilon _{0}}{t_{\mathrm {ox}}} \\[ 5pt ]
&(ヌ)& 2\mathit {\phi }_{\mathrm {F}}+\frac {qN_{\mathrm {A}}l_{\mathrm {Dm}}t_{\mathrm {ox}}}{2\varepsilon _{\mathrm {ox}}\varepsilon _{0}} &(ル)& \frac {qN_{\mathrm {A}}}{2\varepsilon _{\mathrm {s}}\varepsilon _{0}}\left( x-l_{\mathrm {D}}\right) &(ヲ)& \sqrt {\frac {4\mathit {\phi }_{\mathrm {F}}\varepsilon _{\mathrm {ox}}\varepsilon _{0}}{qN_{\mathrm {A}}}} \\[ 5pt ]
&(ワ)& \frac {Qt_{\mathrm {ox}}}{2\varepsilon _{\mathrm {ox}}\varepsilon _{0}} &(カ)& 2\mathit {\phi }_{\mathrm {F}}+\frac {qN_{\mathrm {A}}l_{\mathrm {Dm}}\varepsilon _{\mathrm {ox}}\varepsilon _{0}}{t_{\mathrm {ox}}} &(ヨ)& \sqrt {\frac {4\mathit {\phi }_{\mathrm {F}}\varepsilon _{\mathrm {s}}\varepsilon _{0}}{qN_{\mathrm {A}}}}
\end{eqnarray}
\]
【ワンポイント解説】
半導体工学の教科書に掲載されているような内容で,電験のテキストにはほとんど掲載されないような内容と思います。本問は半分問題にヒントが記載されていますので,半分は数値計算の問題と言えるかもしれません。
【解答】
(1)解答:ハ
\( \ x-l_{\mathrm {D}} =T \ \)とすると
\[
\begin{eqnarray}
\frac {\mathrm {d}T}{\mathrm {d}x} &=& 1\\[ 5pt ]
\end{eqnarray}
\]
であるから,これを用いて問題に与えられている\( \ \displaystyle \frac {\mathrm {d}\mathit {\phi }}{\mathrm {d}x} \ \)を積分すると,
\[
\begin{eqnarray}
\frac {\mathrm {d}\mathit {\phi }}{\mathrm {d}x} &=& \frac {qN_{\mathrm {A}}}{\varepsilon _{\mathrm {s}}\varepsilon _{0}}\left( x-l_{\mathrm {D}}\right) \\[ 5pt ]
\mathrm {d}\mathit {\phi } &=& \frac {qN_{\mathrm {A}}}{\varepsilon _{\mathrm {s}}\varepsilon _{0}}\left( x-l_{\mathrm {D}}\right) \mathrm {d}x \\[ 5pt ]
\mathrm {d}\mathit {\phi } &=& \frac {qN_{\mathrm {A}}}{\varepsilon _{\mathrm {s}}\varepsilon _{0}}T \mathrm {d}T \\[ 5pt ]
\int \mathrm {d}\mathit {\phi } &=& \int \frac {qN_{\mathrm {A}}}{\varepsilon _{\mathrm {s}}\varepsilon _{0}}T \mathrm {d}T \\[ 5pt ]
\mathit {\phi } &=& \frac {qN_{\mathrm {A}}}{2\varepsilon _{\mathrm {s}}\varepsilon _{0}}T^{2} +C (Cは積分定数)\\[ 5pt ]
&=& \frac {qN_{\mathrm {A}}}{2\varepsilon _{\mathrm {s}}\varepsilon _{0}}\left( x-l_{\mathrm {D}}\right) ^{2} +C \\[ 5pt ]
\end{eqnarray}
\]
となり,題意より\( \ x=l_{\mathrm {D}} \ \)において電位が零であるから,\( \ C=0 \ \)となるので
\[
\begin{eqnarray}
\mathit {\phi } &=& \frac {qN_{\mathrm {A}}}{2\varepsilon _{\mathrm {s}}\varepsilon _{0}}\left( x-l_{\mathrm {D}}\right) ^{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:チ
(1)の解答式に\( \ x=0 \ \)を代入すると,
\[
\begin{eqnarray}
\mathit {\phi }_{\mathrm {S}} &=& \frac {qN_{\mathrm {A}}}{2\varepsilon _{\mathrm {s}}\varepsilon _{0}}\left( 0-l_{\mathrm {D}}\right) ^{2} \\[ 5pt ]
&=& \frac {qN_{\mathrm {A}}}{2\varepsilon _{\mathrm {s}}\varepsilon _{0}}{l_{\mathrm {D}}} ^{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:イ
金属とp形半導体間は絶縁体を挟んだ平行平板コンデンサと考えることができるので,絶縁物層内の電界の大きさ\( \ E \ \)は,
\[
\begin{eqnarray}
E &=& \frac {Q}{\varepsilon _{\mathrm {ox}}\varepsilon _{0}} \\[ 5pt ]
\end{eqnarray}
\]
となり,電位差\( \ V \ \)は
\[
\begin{eqnarray}
V &=& Et_{\mathrm {ox}} \\[ 5pt ]
&=& \frac {Qt_{\mathrm {ox}}}{\varepsilon _{\mathrm {ox}}\varepsilon _{0}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ヨ
表面電位\( \ \mathit {\phi }_{\mathrm {S}} \ \)が\( \ 2\mathit {\phi }_{\mathrm {F}} \ \)となった状態がしきい値であるから,(2)より,
\[
\begin{eqnarray}
2\mathit {\phi }_{\mathrm {F}} &=& \frac {qN_{\mathrm {A}}}{2\varepsilon _{\mathrm {s}}\varepsilon _{0}}{l_{\mathrm {D}}} ^{2} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ l_{\mathrm {D}} \ \)について整理すると,
\[
\begin{eqnarray}
l_{\mathrm {D}} &=& \sqrt {\frac {4\mathit {\phi }_{\mathrm {F}}\varepsilon _{\mathrm {s}}\varepsilon _{0}}{qN_{\mathrm {A}}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ホ
(3)より電位差\( \ V \ \)は,
\[
\begin{eqnarray}
V &=& \left| \frac {Qt_{\mathrm {ox}}}{\varepsilon _{\mathrm {ox}}\varepsilon _{0}}\right| \\[ 5pt ]
&=& \frac {qN_{\mathrm {A}}l_{\mathrm {D}}t_{\mathrm {ox}}}{\varepsilon _{\mathrm {ox}}\varepsilon _{0}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,しきい値\( \ T \ \)は,
\[
\begin{eqnarray}
T &=& 2\mathit {\phi }_{\mathrm {F}}+V \\[ 5pt ]
&=& 2\mathit {\phi }_{\mathrm {F}}+\frac {qN_{\mathrm {A}}l_{\mathrm {D}}t_{\mathrm {ox}}}{\varepsilon _{\mathrm {ox}}\varepsilon _{0}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん