《電力・管理》〈水力〉[H25:問1] 水力発電所の年間発電量及び設備利用率に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

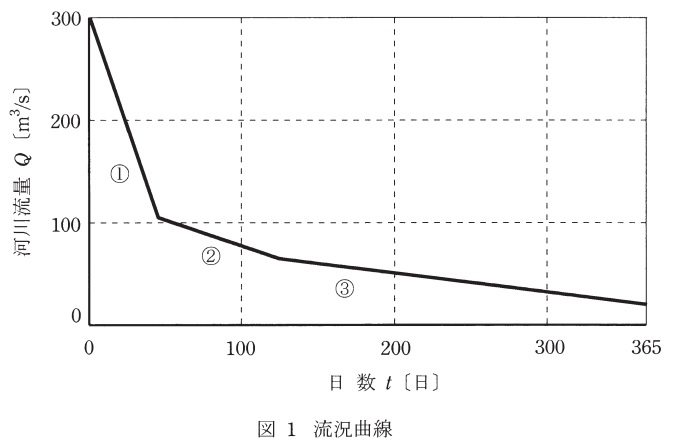
①式～③式の直線近似式で表される図1の流況曲線の河川に，最大取水量\( \ 100 \ \mathrm {[m^{3}／s]} \ \)，最小取水量\( \ 15 \ \mathrm {[m^{3}／s]} \ \)，有効落差\( \ 50 \ \mathrm {[m]} \ \)の自流式(流込み式)水力発電所を設置する場合の年間発電電力量\( \ \mathrm {[kW\cdot h]} \ \)と年間設備利用率\( \ \mathrm {[％]} \ \)を，(1)～(4)の手順に沿って求めよ。

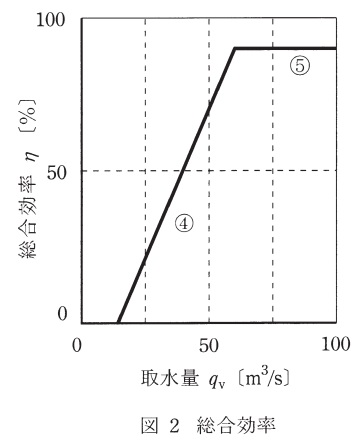
なお，水車・発電機の総合効率\( \ \eta \ \mathrm {[％]} \ \)は，計算の簡便上，取水量の二次式ではなく，図2のような④式及び⑤式の直線近似式によって終日連続運転するものとする。また，年間を通じて，終日\( \ 5 \ \mathrm {[m^{3}／s]} \ \)の河川維持流量を確保するものとする。

ここで，\( \ 1 \ \)年間は\( \ 365 \ \mathrm {[日]} \ \)，水の密度\( \ \rho \ \)は\( \ 1000 \ \mathrm {[kg／m^{3}]} \ \)，重力加速度\( \ \mathit {ｇ} \ \)は\( \ 9.8 \ \mathrm {[m／s^{2}]} \ \)とする。

河川流量\( \ Q \ \mathrm {[m^{3}／s]} \ \)は，日数\( \ t \ \mathrm {[日]} \ \)の関数とし，
\[
\begin{eqnarray}
0&≦t＜&45&のとき&：Q&=&-4.3t+298.5　&　・・・・・・・・・①& \\[ 5pt ] 45&≦t＜&125&のとき&：Q&=&-0.5t+127.5　&　・・・・・・・・・②& \\[ 5pt ] 125&≦t≦&365&のとき&：Q&=&-0.2t+90　&　・・・・・・・・・③& \\[ 5pt ] \end{eqnarray}
\] 総合効率\( \ \eta \ \mathrm {[％]} \ \)は，取水量\( \ q_{\mathrm {v}} \ \mathrm {[m^{3}／s]} \ \)の関数とし，
\[
\begin{eqnarray}
15&≦q_{\mathrm {v}}＜&60&のとき&：\eta &=&2q_{\mathrm {v}}-30　&　・・・・・・・・・④& \\[ 5pt ] 60&≦q_{\mathrm {v}}≦&100&のとき&：\eta &=&90　&　・・・・・・・・・⑤& \\[ 5pt ] \end{eqnarray}
\]

(1)　最大取水量を確保して最大出力で発電できる日数と，最小取水量を確保して発電できる日数をそれぞれ求めよ。

(2)　最大取水量で発電できる期間の累計発電電力量\( \ \mathrm {[kW\cdot h]} \ \)を求めよ。

(3)　最大取水量未満での累計発電電力量\( \ \mathrm {[kW\cdot h]} \ \)を求めよ。

(4)　この発電所の年間発電電力量\( \ \mathrm {[kW\cdot h]} \ \)と，年間設備利用率\( \ \mathrm {[％]} \ \)をそれぞれ求めよ。

【ワンポイント解説】

難易度は１種としてはあまり高くないですが，桁数が大きくなり難しいので，計算間違いに注意が必要な問題となります。どういう場合に最大出力になり，どういう場合に最小出力となるかよく考え，計算間違いに注意しながら解くようにしましょう。

1.水車の理論出力\( \ P \ \)
流量が\( \ Q \ \mathrm {[m^{3} / s]} \ \)，有効落差が\( \ H \ \mathrm {[m]} \ \)，水の密度が\( \ \rho =1000 \ \mathrm {[kg / m^{3}]} \ \)，重力加速度が\( \ g=9.8 \ \mathrm {[m / s^{2}]} \ \)，水車・発電機の総合効率を\( \ \eta \ \)であるとすると，水車の理論出力\( \ P \ \mathrm {[kW]} \ \)は，
\[
\begin{eqnarray}
P &=& \rho gQH\eta \\[ 5pt ] &=& 9.8QH\eta \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められます。

【関連する「電気の神髄」記事】

　　水力発電の計算における基本式

【解答】

(1)最大取水量を確保して最大出力で発電できる日数と，最小取水量を確保して発電できる日数
図1より，最大取水量すなわち\( \ 100 \ \mathrm {[m^{3}／s]} \ \)を確保して最大出力で発電できるのは，終日\( \ 5 \ \mathrm {[m^{3}／s]} \ \)の河川維持流量を確保するため，河川流量\( \ Q \ \mathrm {[m^{3}／s]} \ \)が\( \ 105 \ \mathrm {[m^{3}／s]} \ \)以上の時である。これを①及び②に代入すると，
\[
\begin{eqnarray}
105&=&-4.3t+298.5 \\[ 5pt ] t&=&45 \ \mathrm {[日]} (範囲外) \\[ 5pt ] 105&=&-0.5t+127.5 \\[ 5pt ] t&=&45 \ \mathrm {[日]} (範囲内) \\[ 5pt ] \end{eqnarray}
\] となるので最大取水量を確保して最大出力で発電できる日数は，\( \ 45 \ 日 \ \)である。
一方最小取水量すなわち\( \ 15 \ \mathrm {[m^{3}／s]} \ \)を確保して最大出力で発電できるのは，終日\( \ 5 \ \mathrm {[m^{3}／s]} \ \)の河川維持流量を確保するため，河川流量\( \ Q \ \mathrm {[m^{3}／s]} \ \)が\( \ 20 \ \mathrm {[m^{3}／s]} \ \)以上の時である。これを③に代入すると，
\[
\begin{eqnarray}
20&=&-0.2t+90 \\[ 5pt ] t&=&350 \ \mathrm {[日]} \\[ 5pt ] \end{eqnarray}
\] となるので最小取水量を確保して発電できる日数は，\( \ 350 \ 日 \ \)である。

(2)最大取水量で発電できる期間の累計発電電力量\( \ \mathrm {[kW\cdot h]} \ \)
最大取水量で発電できる発電電力\( \ P_{1} \ \mathrm {[kW]} \ \)は，ワンポイント解説「1.水車の理論出力\( \ P \ \)」の通り，
\[
\begin{eqnarray}
P_{1}&=&9.8QH\eta \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] で求められる。ここで，有効落差\( \ H=50 \ \mathrm {[m]} \ \)であり，図2より，\( \ \eta =0.9 \ \)であるから，
\[
\begin{eqnarray}
P_{1}&=&9.8\times 100 \times 50 \times 0.9 \\[ 5pt ] &=&44 \ 100 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] となる。(1)より，最大取水量を確保して最大出力で発電できる日数は，\( \ 45 \ 日 \ \)なので，最大取水量で発電できる期間の累計発煙電力量\( \ W_{1} \ \mathrm {[kW\cdot h]} \ \)は，
\[
\begin{eqnarray}
W_{1}&=&P_{1}\times 24\times 45 \\[ 5pt ] &=&44 \ 100\times 24\times 45 \\[ 5pt ] &=&47 \ 628 \ 000　→　47 \ 600 \ 000 \ \mathrm {[kW\cdot h]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)最大取水量未満での累計発電電力量\( \ \mathrm {[kW\cdot h]} \ \)
最大取水量未満での累計発電電力量として求めるのは(1)より，\( \ 45≦t≦350 \ \)の範囲である。
ここで，総合効率が④のように流量に比例する関数が適用されるのは，取水量が\( \ 60 \ \mathrm {[m^{3}／s]} \ \)未満の時であるので，\( \ Q=65 \ \)を③に代入すると，
\[
\begin{eqnarray}
65&=&-0.2t+90 \\[ 5pt ] t&=&125 \ \mathrm {[日]} \\[ 5pt ] \end{eqnarray}
\] と求められる。したがって，今回の計算では，\( \ 45≦t ＜ 125 \ \)の時及び\( \ 125≦t≦350 \ \)の時の計算を分けて考える。\( \ 45≦t＜125 \ \)の時\( \ \eta =0.9 \ \)であるから，発電できる発電電力\( \ P_{2} \ \mathrm {[kW]} \ \)は，
\[
\begin{eqnarray}
P_{2}&=& 9.8QH \eta \\[ 5pt ] &=&9.8\times \left( -0.5t+127.5-5 \right) \times 50 \times 0.9 \\[ 5pt ] &=&-220.5t +54022.5 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] となるので，この期間の発電電力量\( \ W_{2} \ \mathrm {[kW \cdot h]} \ \)は，
\[
\begin {eqnarray}
W_{2}&=&\int _{45}^{125}\left( P_{2}\times 24 \right) \ \mathrm {d}t \\[ 5pt ] &=&\int _{45}^{125}\left( -5292 t + \mathrm {1 296 540} \right) \ \mathrm {d}t \\[ 5pt ] &=&\left[ -2646t^{2} + 1296540t \right] _{45}^{125} \\[ 5pt ] &=& -41 \ 343 \ 750 + 162 \ 067 \ 500 + 5 \ 358 \ 150-58 \ 344 \ 300 \\[ 5pt ] &=&67 \ 737 \ 600 \ \mathrm {[kW\cdot h]} \\[ 5pt ] \end {eqnarray}
\] と求められる。次に，\( \ 125≦t≦350 \ \)の時，発電できる発電電力\( \ P_{3} \ \mathrm {[kW]} \ \)は，
\[
\begin{eqnarray}
P_{3}&=& 9.8QH\eta \\[ 5pt ] &=&9.8\times \left( -0.2t+90-5 \right) \times 50 \times \frac {2Q-30}{100} \\[ 5pt ] &=&9.8\times \left( -0.2t+90-5 \right) \times 50 \times \frac {2\left( -0.2t+90-5 \right) -30}{100} \\[ 5pt ] &=&4.9 \left( 0.08t^{2}-62t+11900 \right) \\[ 5pt ] &=&0.392t^{2}-303.8t +58310 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] となるので，この期間の発電電力量\( \ W_{3} \ \mathrm {[kW\cdot h]} \ \)は，
\[
\begin{eqnarray}
W_{3}&=&\int _{125}^{350}P_{3}\times 24 \ \mathrm {d}t \\[ 5pt ] &=&\int _{125}^{350}9.408t^{2}-7291.2t +\mathrm {1399440} \ \mathrm {d}t \\[ 5pt ] &=&\left[ 3.136t^{3}-3645.6t^{2} +1399440t\right] _{125}^{350} \\[ 5pt ] &=&\left[ 134 \ 456 \ 000-446 \ 586 \ 000+489 \ 804 \ 000-6 \ 125 \ 000+56 \ 962 \ 500-174 \ 930 \ 000\right] \\[ 5pt ] &=&53 \ 581 \ 500 \ \mathrm {[kW\cdot h]} \\[ 5pt ] \end{eqnarray}
\] と求められる。したがって，最大取水量未満での累計発電電力量は，
\[
\begin{eqnarray}
W_{2}+W_{3}&=&67 \ 737 \ 600+53 \ 581 \ 500 \\[ 5pt ] &=&121 \ 319 \ 100　→　121 \ 000 \ 000 \ \mathrm {[kW\cdot h]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)年間発電電力量\( \ \mathrm {[kW\cdot h]} \ \)と年間設備利用率\( \ \mathrm {[％]} \ \)
(2)，(3)より年間発電電力量\( \ W_{4} \ \)は，
\[
\begin{eqnarray}
W_{4}&=&W_{1}+W_{2}+W_{3} \\[ 5pt ] &=&47 \ 628 \ 000+121 \ 319 \ 100 \\[ 5pt ] &=&168 \ 947 \ 100　→　169 \ 000 \ 000 \ \mathrm {[kW\cdot h]} \\[ 5pt ] \end{eqnarray}
\] と求められる。水力発電所が年間で発電可能な発電電力量\( \ W_{5} \ \)は，最大電力で365日運転した時の電力量であるから，
\[
\begin{eqnarray}
W_{5}&=&P_{1}\times 24\times 365 \\[ 5pt ] &=&44 \ 100\times 24\times 365 \\[ 5pt ] &=&386 \ 316 \ 000 \ \mathrm {[kW\cdot h]} \\[ 5pt ] \end{eqnarray}
\] であるから，設備利用率\( \ \eta _{\mathrm {m}} \ \)は，
\[
\begin{eqnarray}
\eta _{\mathrm {m}}&=&\frac {W_{4}}{W_{5}}\times 100 \\[ 5pt ] &=&\frac {168 \ 947 \ 100}{386 \ 316 \ 000}\times 100 \\[ 5pt ] &≒&43.733　→　43.7 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。