【問題】
【難易度】★★★★☆(やや難しい)
図1および図2は水車ランナ内における水の流れを表している。水の流れが①から②への中心流線によって代表されるものとしたとき,(1)から(4)の問は与えられた記号を用いて式で表し,(5)は数値計算せよ。
なお,ガイドベーンは図1の状況が全周にわたって均等にあるものとし,水車全体に対する水の流量,有効落差,水の密度及び重力加速度は,それぞれ\( \ q_{\mathrm {v}} \ \mathrm {[m^{3}/s]} \ \),\( \ H \ \mathrm {[m]} \ \),\( \ \rho \ \mathrm {[kg/m^{3}]} \ \)及び\( \ g \ \mathrm {[m/s^{2}]} \ \)とする。
ただし,ランナ固定部から漏れる流水および機械損失は無視する。

【凡例】
\(v_{1}\) :ランナ入口①における水の流入速度\( \ \mathrm {[m / s]} \ \)
\(v_{2}\) :ランナ出口②における水の流出速度\( \ \mathrm {[m / s]} \ \)
\(u_{1}\) :ランナ入口①の周速度\( \ \mathrm {[m / s]} \ \)
\(u_{2}\) :ランナ出口②の周速度\( \ \mathrm {[m / s]} \ \)
\(w_{1}\) :ランナ入口①における水のランナに対する相対速度\( \ \mathrm {[m / s]} \ \)
\(w_{2}\) :ランナ出口②における水のランナに対する相対速度\( \ \mathrm {[m / s]} \ \)
\(\alpha _{1}\) :ランナ入口①における水の流入速度と周速度のなす角度\( \ \mathrm {[rad]} \ \)
\(\alpha _{2}\) :ランナ出口②における水の流出速度と周速度のなす角度\( \ \mathrm {[rad]} \ \)
\(r_{1} \ \) :ランナ中心からランナ入口①までの半径\( \ \mathrm {[m]} \ \)
\(r_{2} \ \) :ランナ中心からランナ出口②までの半径\( \ \mathrm {[m]} \ \)
(1) ランナ入口①における流速の回転方向(周速度方向)成分は,ランナ入口の水の流入速度\( \ v_{1} \ \mathrm {[m / s]} \ \)に比例する。その大きさを求めるとともに,図3の速度線図を答案用紙に書き写し,そのベクトルを記入せよ。
(2) ランナに発生するトルクは,流水のランナ入口①と出口②における回転方向(周速度方向)の単位時間当たりの運動量のモーメントの差となる。この関係を用いて流水がランナに与えるトルク\( \ T \ \mathrm {[N\cdot m]} \ \)を求めよ。
(3) ランナ出力は,流水がランナに与えるトルクとランナの角速度の積で表すことができる。この関係を用いてランナ出力\( \ P \ \mathrm {[kW]} \ \)を求めよ。
(4) (3)のランナ出力からランナ効率\( \ \eta \ [%] \ \)を求め,ランナ出口②における水の流出速度と周速度のなす角度\( \ \alpha _{2} \ \mathrm {[rad]} \ \)をパラメータとしたときの理論上最大となる効率\( \ \eta \ [%] \ \)とそのときの角度\( \ \alpha _{2} \ \mathrm {[rad]} \ \)を求めよ。
(5) (4)の場合において,次の条件における理論上最大効率\( \ \eta \ [%] \ \)を計算せよ。

【ワンポイント解説】
水力発電の計算問題は比較的理解しやすい問題が多いですが,(1)で躓くとその後の計算が合っていても全て誤答になってしまう危険性を持っています(記述式である以上0点になることはないと思いますが)。過去問を何度も取り組み,ケアレスミスを防止するようにしましょう。
【解答】
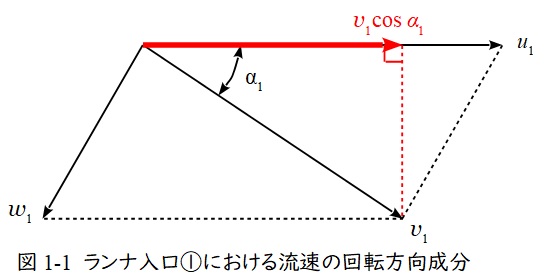
(1)ランナ入口①における流速の回転方向(周速度方向)成分の大きさとそのベクトル
流速の回転方向(周速度成分)はベクトル図1-1の通りでありこれより\( \ v_{1}\cos \alpha_{1} \ \mathrm {[m / s]} \ \)と求められる。
(2)流水がランナに与えるトルク\( \ T \ \mathrm {[N\cdot m]} \ \)
ランナ入口①での運動量\( \ p_{1} \ \)は,単位時間あたりの質量流量\( \ Q \ \)と周速度\( \ v_{1}\cos \alpha_{1} \ \)の積であり,題意より\( \ Q=\rho q_{\mathrm {v}} \ \)であるから,運動量のモーメント\( \ L_{1} \ \)は,
\[
\begin{eqnarray}
L_{1}&=&p_{1} \cdot r_{1} \\[ 5pt ]
&=&Qv_{1}\cos \alpha_{1} \cdot r_{1} \\[ 5pt ]
&=&\rho q_{\mathrm {v}}r_{1}v_{1}\cos \alpha_{1} \\[ 5pt ]
\end{eqnarray}
\]
となる。同様に,ランナ出口②での運動量のモーメント\( \ L_{2} \ \)は,運動量\( \ p_{2} \ \),周速度\( \ v_{2}\cos \alpha_{2} \ \)を用いて,
\[
\begin{eqnarray}
L_{2}&=&p_{2} \cdot r_{2} \\[ 5pt ]
&=&Qv_{2}\cos \alpha_{2} \cdot r_{2} \\[ 5pt ]
&=&\rho q_{\mathrm {v}}r_{2}v_{2}\cos \alpha_{2} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,流水がランナに与えるトルク\( \ T \ \)は\( \ L_{1} \ \)と\( \ L_{2} \ \)の差であるから,
\[
\begin{eqnarray}
T&=&L_{1}-L_{2} \\[ 5pt ]
&=&\rho q_{\mathrm {v}}r_{1}v_{1}\cos \alpha_{1}-\rho q_{\mathrm {v}}r_{2}v_{2}\cos \alpha_{2} \\[ 5pt ]
&=&\rho q_{\mathrm {v}}\left( r_{1}v_{1}\cos \alpha_{1}-r_{2}v_{2}\cos \alpha_{2} \right) \ \mathrm {[N\cdot m]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)ランナ出力\( \ P \ \mathrm {[kW]} \ \)
題意より,\( \ P \ \mathrm {[kW]}=\omega T\times 10^{-3} \ \)であるから,
\[
\begin{eqnarray}
P&=&\omega T\times 10^{-3} \\[ 5pt ]
&=&\omega \rho q_{\mathrm {v}}\left( r_{1}v_{1}\cos \alpha_{1}-r_{2}v_{2}\cos \alpha_{2} \right)\times 10^{-3} \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで\( \ u_{1}=r_{1}\omega \ \),\( \ u_{2}=r_{2}\omega \ \)であるから,
\[
\begin{eqnarray}
P&=&\rho q_{\mathrm {v}}\left( \frac {u_{1}}{r_{1}}\cdot r_{1}v_{1}\cos \alpha_{1}-\frac {u_{2}}{r_{2}}\cdot r_{2}v_{2}\cos \alpha_{2} \right)\times 10^{-3} \\[ 5pt ]
&=&\rho q_{\mathrm {v}}\left( u_{1}v_{1}\cos \alpha_{1}-u_{2}v_{2}\cos \alpha_{2} \right)\times 10^{-3} \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)ランナ効率\( \ \eta \ [%] \ \)及び理論上最大となる効率\( \ \eta \ [%] \ \)とそのときの角度\( \ \alpha _{2} \ \mathrm {[rad]} \ \)
ランナ入口の入力を\( \ P_{0} \ \)とすると,重力加速度\( \ g \ \),単位時間あたりの質量流量\( \ Q=\rho q_{\mathrm {v}} \ \),有効落差\( \ H \ \)を用いて,
\[
\begin{eqnarray}
P_{0}&=&gQH\times 10^{-3} \\[ 5pt ]
&=&g\rho q_{\mathrm {v}}H\times 10^{-3} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,ランナ効率\( \ \eta \ \)は,
\[
\begin{eqnarray}
\eta &=&\frac {P}{P_{0}}\times 100 \\[ 5pt ]
&=&\frac {\rho q_{\mathrm {v}}\left( u_{1}v_{1}\cos \alpha_{1}-u_{2}v_{2}\cos \alpha_{2} \right)\times 10^{-3}}{g\rho q_{\mathrm {v}}H\times 10^{-3}}\times 100 \\[ 5pt ]
&=&\frac {u_{1}v_{1}\cos \alpha_{1}-u_{2}v_{2}\cos \alpha_{2}}{gH}\times 100 \ [%] \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
次に,角度\( \ \alpha _{2} \ \mathrm {[rad]} \ \)をパラメータとしたときの理論上最大となる効率\( \ \eta_{\max} \ \)を求める。水車の構造上\( \ \displaystyle 0≦\alpha _{2}≦\frac{\pi}{2} \ \)であるため,最大効率を得るのは,\( \ \cos \alpha_{2}=0 \ \)すなわち,\( \ \displaystyle \alpha_{2}=\frac{\pi}{2} \ \)の時である。
よって,最大となる効率\( \ \eta_{\max} \ \)は,
\[
\begin{eqnarray}
\eta_{\max}&=&\frac {u_{1}v_{1}\cos \alpha_{1}}{gH}\times 100 \ [%] \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)与えられた条件における理論上最大効率\( \ \eta \ [%] \ \)
(4)の解答式において未知数\( \ u_{1} \ \)を(5)の表の値を用いて表すと,\( \ u_{1}=2\pi r_{1}n \ \)である。よって(4)解答式を変形し,各値を代入すれば,
\[
\begin{eqnarray}
\eta_{\max}&=&\frac {u_{1}v_{1}\cos \alpha_{1}}{gH}\times 100 \\[ 5pt ]
&=&\frac {2\pi r_{1}nv_{1}\cos \alpha_{1}}{gH}\times 100 \\[ 5pt ]
&=&\frac {2\pi \times 0.5 \times 10\times 35 \times \cos 30°}{9.8 \times 100}\times 100 \\[ 5pt ]
&≒&97.2 \ [%] \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん