【問題】
【難易度】★★☆☆☆(やや易しい)
図に示すような送電系統において,次の問に答えよ。
ただし,単位は表記のない場合は,系統容量\( \ 1000 \ \mathrm {MV\cdot A} \ \),系統定格電圧を基準とする単位法\( \ \mathrm {[p.u.]} \ \)とする。
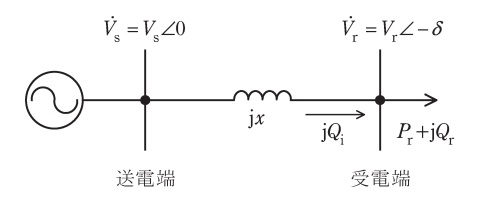
\[
\begin{eqnarray}
&{\dot V}_{\mathrm {s}}&&:& 送電端電圧 &P_{\mathrm {r}}&&:& 負荷の有効電力 \\[ 5pt ]
&{\dot V}_{\mathrm {r}}&&:& 受電端電圧 &Q_{\mathrm {r}}&&:& 負荷の無効電力 \\[ 5pt ]
&x&&:& 送電線のリアクタンス &\delta &&:& 送電端と受電端の電圧位相差角 \ \mathrm {[rad]} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
&Q_{\mathrm {i}}&&:& 送電端から受電端に流入する無効電力 \\[ 5pt ]
\end{eqnarray}
\]
(1) \( \ Q_{\mathrm {i}} \ \)を\( \ V_{\mathrm {s}} \ \),\( \ V_{\mathrm {r}} \ \),\( \ x \ \)及び\( \ \delta \ \)で表す式を求めよ。ただし,遅れ無効電力を正とする。
(2) \( \ \delta \ \)は十分に小さいとして\( \ P_{\mathrm {r}} \ \)による\( \ {\dot V}_{\mathrm {r}} \ \)の大きさの変化を考えなければ,\( \ Q_{\mathrm {i}} \ \)と\( \ Q_{\mathrm {r}} \ \)が等しくなる条件で受電端電圧の大きさ\( \ V_{\mathrm {r}} \ \)が決まる。\( \ Q_{\mathrm {r}} \ \)が\( \ V_{\mathrm {r}}=1.0 \ \)付近で次式による特性を持つ場合,\( \ V_{\mathrm {r}} \ \)と\( \ Q_{\mathrm {r}} \ \mathrm {[Mvar]} \ \)を求めよ。
\[
\begin{eqnarray}
Q_{\mathrm {r}}&=&4V_{\mathrm {r}}-3 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
(負荷の自己容量\( \ 600 \ \mathrm {MV\cdot A} \ \)を基準,定格電圧は送電系統に同じ)
ただし,送電端の\( \ V_{\mathrm {s}} \ \)は常に\( \ 1.0 \ \)とし,\( \ x \ \)は\( \ 0.03 \ \)とする。
【ワンポイント解説】
(1)は1種では頻出問題である送電電力の導出,(2)は単位法の計算となります。途中の計算は少し手間がかかりますが,1種としては比較的易しめの問題となるので,確実に理解しておくようにしておきましょう。
1.オイラーの公式
極座標空間において,
\[
\begin{eqnarray}
\mathrm {e}^{\mathrm {j}\theta }&=&\cos \theta +\mathrm {j}\sin \theta \\[ 5pt ]
\end{eqnarray}
\]
となります。したがって,\( \ {\dot V}_{\mathrm {s}}= V_{\mathrm {s}}∠0 \ \),\( \ {\dot V}_{\mathrm {r}}= V_{\mathrm {r}}∠-\delta \ \)は,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {s}}&=&V_{\mathrm {s}} \\[ 5pt ]
{\dot V}_{\mathrm {r}}&=&V_{\mathrm {r}}\left\{ \cos \left(-\delta \right)+\mathrm {j}\sin \left(-\delta \right)\right\} \\[ 5pt ]
&=&V_{\mathrm {r}}\left( \cos \delta -\mathrm {j}\sin \delta \right) \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)\( \ Q_{\mathrm {i}} \ \)を\( \ V_{\mathrm {s}} \ \),\( \ V_{\mathrm {r}} \ \),\( \ x \ \)及び\( \ \delta \ \)で表す式
送電線を流れる電流を\( \ \dot I \ \)とすると,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {s}}&=&{\dot V}_{\mathrm {r}}+\mathrm {j}x{\dot I} \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,ワンポイント解説「1.オイラーの公式」より,\( \ {\dot V}_{\mathrm {s}}=V_{\mathrm {s}} \ \),\( \ {\dot V}_{\mathrm {r}}=V_{\mathrm {r}}\left( \cos \delta -\mathrm {j}\sin \delta \right) \ \)であるから,
\[
\begin{eqnarray}
V_{\mathrm {s}}&=&V_{\mathrm {r}}\left( \cos \delta -\mathrm {j}\sin \delta \right) +\mathrm {j}x{\dot I} \\[ 5pt ]
\mathrm {j}x{\dot I}&=&V_{\mathrm {s}}-V_{\mathrm {r}}\left( \cos \delta -\mathrm {j}\sin \delta \right) \\[ 5pt ]
\dot I&=&\frac {V_{\mathrm {s}}-V_{\mathrm {r}}\left( \cos \delta -\mathrm {j}\sin \delta \right) }{\mathrm {j}x} \\[ 5pt ]
&=&\frac {V_{\mathrm {r}}\sin \delta }{x}-\mathrm {j}\frac {V_{\mathrm {s}}-V_{\mathrm {r}}\cos \delta }{x} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,送電端から受電端への送電電力\( \ P_{\mathrm {i}}+\mathrm {j}Q_{\mathrm {i}} \ \)は遅れ無効電力を正とすると,
\[
\begin{eqnarray}
P_{\mathrm {i}}+\mathrm {j}Q_{\mathrm {i}}&=&{\dot V}_{\mathrm {r}}\overline {\dot I} \\[ 5pt ]
&=&V_{\mathrm {r}}\left( \cos \delta -\mathrm {j}\sin \delta \right) \left( \frac {V_{\mathrm {r}}\sin \delta }{x}+\mathrm {j}\frac {V_{\mathrm {s}}-V_{\mathrm {r}}\cos \delta }{x}\right) \\[ 5pt ]
&=&V_{\mathrm {r}}\left\{ \left( \frac {V_{\mathrm {r}}\sin \delta \cos \delta }{x}+\frac {V_{\mathrm {s}}\sin \delta -V_{\mathrm {r}}\sin \delta \cos \delta }{x} \right) +\mathrm {j}\left( -\frac {V_{\mathrm {r}}\sin ^{2}\delta }{x}+\frac {V_{\mathrm {s}}\cos \delta -V_{\mathrm {r}}\cos ^{2}\delta }{x}\right) \right\} \\[ 5pt ]
&=&V_{\mathrm {r}}\left\{ \frac {V_{\mathrm {s}}\sin \delta }{x} +\mathrm {j}\frac {V_{\mathrm {s}}\cos \delta -V_{\mathrm {r}}\left( \sin ^{2}\delta +\cos ^{2}\delta \right) }{x}\right\} \\[ 5pt ]
&=&V_{\mathrm {r}}\left( \frac {V_{\mathrm {s}}\sin \delta }{x} +\mathrm {j}\frac {V_{\mathrm {s}}\cos \delta -V_{\mathrm {r}}}{x}\right) \\[ 5pt ]
&=&\frac {V_{\mathrm {s}}V_{\mathrm {r}}\sin \delta }{x} +\mathrm {j}\frac {V_{\mathrm {s}}V_{\mathrm {r}}\cos \delta -V_{\mathrm {r}}^{2}}{x} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ Q_{\mathrm {i}} \ \)は,
\[
\begin{eqnarray}
Q_{\mathrm {i}}&=&\frac {V_{\mathrm {s}}V_{\mathrm {r}}\cos \delta -V_{\mathrm {r}}^{2}}{x} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)\( \ Q_{\mathrm {r}} \ \)が\( \ V_{\mathrm {r}}=1.0 \ \)付近で題意の特性を持つ場合,\( \ V_{\mathrm {r}} \ \)と\( \ Q_{\mathrm {r}} \ \mathrm {[Mvar]} \ \)
題意より,\( \ \delta \ \)は十分に小さいので,
\[
\begin{eqnarray}
\cos \delta &≒&1 \\[ 5pt ]
\end{eqnarray}
\]
となり,(1)の解答式は,\( \ Q_{\mathrm {i}} = Q_{\mathrm {r}} \ \)の条件から,
\[
\begin{eqnarray}
Q_{\mathrm {r}}&=&\frac {V_{\mathrm {s}}V_{\mathrm {r}}-V_{\mathrm {r}}^{2}}{x} \\[ 5pt ]
\end{eqnarray}
\]
と変換できる。これに,\( \ V_{\mathrm {s}}=1.0 \ \),\( \ x=0.03 \ \)を代入すると,
\[
\begin{eqnarray}
Q_{\mathrm {r}}&=&\frac {V_{\mathrm {r}}-V_{\mathrm {r}}^{2}}{0.03} \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,\( \ Q_{\mathrm {r}}=4V_{\mathrm {r}}-3 \ \)は\( \ 600 \ \mathrm {MV\cdot A} \ \)基準であるから,\( \ 1000 \ \mathrm {MV\cdot A} \ \) 基準にすると,
\[
\begin{eqnarray}
Q_{\mathrm {r}}&=&\left( 4V_{\mathrm {r}}-3\right) \frac {600}{1000} \\[ 5pt ]
&=&2.4V_{\mathrm {r}}-1.8 \\[ 5pt ]
\end{eqnarray}
\]
となるので,これを代入し\( \ V_{\mathrm {r}} \ \)を求めると,
\[
\begin{eqnarray}
2.4V_{\mathrm {r}}-1.8 &=&\frac {V_{\mathrm {r}}-V_{\mathrm {r}}^{2}}{0.03} \\[ 5pt ]
0.072V_{\mathrm {r}}-0.054&=&V_{\mathrm {r}}-V_{\mathrm {r}}^{2} \\[ 5pt ]
V_{\mathrm {r}}^{2}-0.928V_{\mathrm {r}}-0.054&=&0 \\[ 5pt ]
1000V_{\mathrm {r}}^{2}-928V_{\mathrm {r}}-54&=&0 \\[ 5pt ]
V_{\mathrm {r}}&=&\frac {464±\sqrt {464^{2}+1000\times 54}}{1000} \\[ 5pt ]
&≒&\frac {464±518.94}{1000} \\[ 5pt ]
&=&0.98294,-0.05494(不適) → 0.983 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。これより,
\[
\begin{eqnarray}
Q_{\mathrm {r}}&=&2.4\times 0.98294-1.8 \\[ 5pt ]
&≒&0.55906 \ \mathrm {[p.u.]} \\[ 5pt ]
&≒&559.06 → 559 \ \mathrm {[Mvar]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん