《理論》〈電気回路〉[R2:問10]テブナンの定理を利用した過渡現象に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

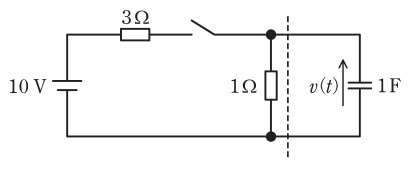
図の回路のスイッチを閉じたあとの電圧\( \ v \left( t \right) \ \)の波形を考える。破線から左側にテブナンの定理を適用することで，回路の時定数\( \ \mathrm {[s]} \ \)と\( \ v \left( t \right) \ \)の最終値\( \ \mathrm {[V]} \ \)の組合せとして，最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし，初めスイッチは開いており，回路は定常状態にあったとする。

\[
\begin{array}{ccc}
& 時定数 \ \mathrm {[s]} \ & 最終値 \ \mathrm {[V]} \ \\
\hline
(1) & 0.75 & 10 \\
\hline
(2) & 0.75 & 2.5 \\
\hline
(3) & 4 & 2.5 \\
\hline
(4) & 1 & 10 \\
\hline
(5) & 1 & 0 \\
\hline
\end{array}
\]

【ワンポイント解説】

テブナンの定理と過渡現象を複合したやや応用的な問題であると思います。当然過渡現象の回路においてもテブナンの定理は成立するので，両方の内容をしっかりと理解していれば解ける問題であると思います。

1.合成抵抗
抵抗\( \ R_{1} \ \)と\( \ R_{2} \ \)が与えられている時，それぞれの合成抵抗\( \ R \ \)は以下の式で与えられます。

①直列
直列合成抵抗\( \ R \ \)は，
\[
\begin{eqnarray}
R&=&R_{1}+R_{2} \\[ 5pt ] \end{eqnarray}
\] となります。

②並列
並列合成抵抗\( \ R \ \)は，
\[
\begin{eqnarray}
\frac {1}{R}&=&\frac {1}{R_{1}}+\frac {1}{R_{2}} \\[ 5pt ] \end{eqnarray}
\] となり，整理すると，
\[
\begin{eqnarray}
R&=&\frac {R_{1}R_{2}}{R_{1}+R_{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

2.テブナンの定理
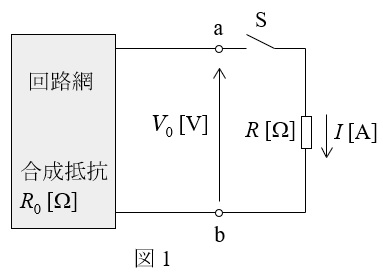
下図のような回路において，端子\( \ \mathrm {a-b} \ \)の開放電圧を\( \ V_{\mathrm {0}} \ \mathrm {[V]} \ \)，端子\( \ \mathrm {a-b} \ \)から電源側をみた合成抵抗を\( \ R_{\mathrm {0}} \ \mathrm {[\Omega ]} \ \)とする（ただし，電圧源は短絡，電流源は開放する）と，図の抵抗\( \ R \ \mathrm {[\Omega ]} \ \)を流れる電流の大きさ\( \ I \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I&=&\frac {V_{\mathrm {0}}}{R+R_{0}} \\[ 5pt ] \end{eqnarray}
\] で求められます。

3.過渡現象におけるリアクトルの過渡状態と定常状態
① 過渡状態
リアクトルに流れる電流値を維持しようとする働きをします。したがって，リアクトルに電圧を印加した瞬間はほとんど電流は流れないので，開放として考えます。

② 定常状態
電圧を印加して十分時間が経過した後は，リアクトルの抵抗はほぼ零になります。したがって，短絡として考えます。

4.過渡現象におけるコンデンサの過渡状態と定常状態
① 過渡状態
コンデンサに蓄えられている電荷が零であるので，電流がものすごく流れやすい状態，すなわち短絡として考えます。

② 定常状態
コンデンサに十分に電荷が蓄えられているので，電流をこれ以上蓄えようとしない，すなわち開放として考えます。

5.時定数
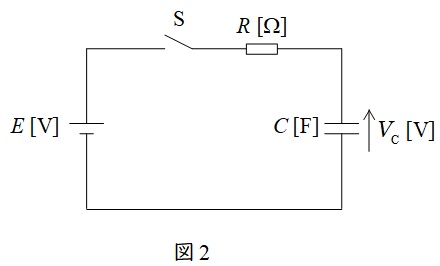
過渡現象におけるコンデンサ電圧の導出は微分方程式の計算を伴うため二種以上の範囲となりますが，図のような回路が与えられると，コンデンサ電圧\( \ V_{\mathrm {C}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {C}} &=&E\left( 1-\mathrm {e}^{-\frac {t}{CR}}\right) \\[ 5pt ] \end{eqnarray}
\] で与えられ，\( \ t=CR \ \)となる時間を時定数\( \ \tau \ \)と呼びます。

【関連する「電気の神髄」記事】

　　RC並列回路の過渡現象（直流回路）

【解答】

解答：(2)
ワンポイント解説「2.テブナンの定理」より，破線部の開放電圧\( \ V_{\mathrm {0}} \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {0}}&=&\frac {1}{3+1}\times 10 \\[ 5pt ] &=&2.5 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] であり，破線から電源側をみた合成抵抗\( \ R_{\mathrm {0}} \ \mathrm {[\Omega ]} \ \)は，電圧源を短絡すると，
\[
\begin{eqnarray}
R_{\mathrm {0}}&=&\frac {3\times 1}{3+1} \\[ 5pt ] &=&0.75 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] であるから，回路は図3のように書き換えられる。

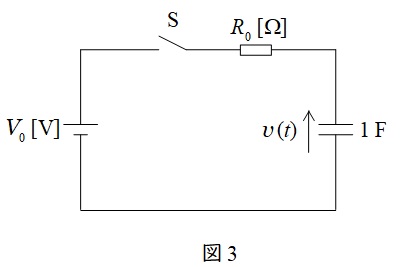
以上から，時定数\( \ \tau \ \)は，ワンポイント解説「5.時定数」より，
\[
\begin{eqnarray}
\tau &=&CR_{\mathrm {0}} \\[ 5pt ] &=&1\times 0.75 \\[ 5pt ] &=&0.75 \mathrm {[s]} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ v \left( t \right) \ \)の最終値は，ワンポイント解説「4.過渡現象におけるコンデンサの過渡状態と定常状態」より，開放状態すなわちすべての電圧がかかるから，
\[
\begin{eqnarray}
V_{\mathrm {C}}&=&V_{\mathrm {0}} \\[ 5pt ] &=&2.5 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。