【問題】
【難易度】★★★★☆(やや難しい)
図1に示す制御対象と図2に示すフィードバック制御系について,次の問に答えよ。ただし,\( \ U\left( s\right) \ \)は操作量,\( \ X_{1}\left( s\right) \ \),\( \ X_{2}\left( s\right) \ \)は状態変数,\( \ Y\left( s\right) \ \)は出力,\( \ R\left( s\right) \ \)は目標値,\( \ E\left( s\right) \ \)は偏差を表し,時間信号\( \ u\left( t\right) \ \),\( \ x_{1}\left( t\right) \ \),\( \ x_{2}\left( t\right) \ \),\( \ y\left( t\right) \ \),\( \ r\left( t\right) \ \),\( \ e\left( t\right) \ \)をそれぞれラプラス変換したものである。
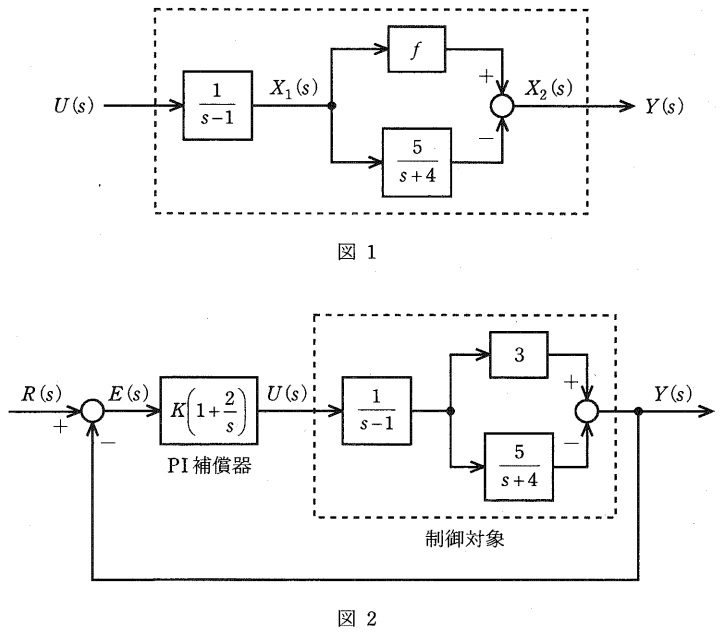
(1) 図1において,\( \ f = 1 \ \)とおく。このとき,状態変数\( \ x_{1}\left( t\right) \ \),\( \ x_{2}\left( t\right) \ \)を図1のように選んだときの状態空間表現\( \ \left( \boldsymbol A,\boldsymbol b,\boldsymbol c ^{\mathrm {T}}\right) \ \),すなわち
\[
\begin{eqnarray}
\frac {\mathrm {d}}{\mathrm {d}t}\boldsymbol x \left( t \right) &=& \boldsymbol A \boldsymbol x \left( t \right) +\boldsymbol b u \left( t \right) \\[ 5pt ]
y \left( t \right) &=& \boldsymbol c ^{\mathrm {T}}\boldsymbol x \left( t \right) \\[ 5pt ]
\end{eqnarray}
\]
を与える\( \ \displaystyle \boldsymbol A=\begin{bmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{bmatrix} \ \),\( \ \displaystyle \boldsymbol b=\begin{bmatrix}
b_{1} \\
b_{2}
\end{bmatrix} \ \),\( \ \displaystyle \boldsymbol c ^{\mathrm {T}}=\begin{bmatrix}
c_{1} & c_{2}
\end{bmatrix} \ \)を求めよ。ただし,\( \ \displaystyle \boldsymbol x \left( t \right) =\begin{bmatrix}
x_{1}\left( t \right) \\
x_{2}\left( t \right)
\end{bmatrix} \ \)とおいた。
(2) 上記(1)で求めた状態空間表現の可制御性,可観測性及び\( \ u\left( t\right) =0 \ \)のときの原点\( \ \displaystyle \boldsymbol x =\begin{bmatrix}
0 \\
0
\end{bmatrix} \ \)の周りの安定性について,それぞれ判定し,その判定の根拠を述べよ。
(3) 次に,\( \ f=3 \ \)とおいた図1の制御対象を含む図2のフィードバック制御系について考える。この制御系が安定となるための\( \ K \ \)の範囲を求めよ。ただし,答は平方根を含む形でよい。
(4) 図2のフィードバック制御系が安定であるとき,目標値\( \ r\left( t\right) =t \ \)に対する定常偏差を\( \ K \ \)を用いて表せ。ただし,\( \ t≧0 \ \)である。
【ワンポイント解説】
現代制御理論も絡めたフィードバック制御の計算問題です。
非常に計算量,作業量が多く,\( \ 30 \ \)分で解くのは困難な問題ではないかと思います。
多くの公式を扱うため現代制御理論の公式や考え方等の勉強にはとても有意義な問題となりますので,試験勉強としてはオススメの問題です。
1.基本的なラプラス変換
\( \ f(t) \ \)のラプラス変換を\( \ F(s) \ \)とすると以下のような関係があります。
\[
\begin{array}{|c|c|}
\hline
f(t) & F(s) \\
\hline
{\displaystyle \delta (t) }\atop{単位インパルス関数} & 1 \\[ 5pt ]
{\displaystyle u (t) }\atop{単位ステップ関数} & \displaystyle \frac {1}{s} \\[ 5pt ]
K & \displaystyle \frac {K}{s} \\[ 5pt ]
t & \displaystyle \frac {1}{s^{2}} \\[ 5pt ]
\mathrm {e}^{at} & \displaystyle \frac {1}{s-a} \\[ 5pt ]
\sin \omega t & \displaystyle \frac {\omega }{s^{2}+\omega ^{2}} \\[ 5pt ]
\cos \omega t & \displaystyle \frac {s}{s^{2}+\omega ^{2}} \\[ 5pt ]
\displaystyle \frac {\mathrm {d}f\left( t \right) }{\mathrm {d}t} & sF\left( s \right) -f\left( 0 \right) \\[ 5pt ]
\displaystyle \int f\left( t \right) \mathrm {d}t & \displaystyle \frac {F\left( s \right) }{s}+\frac {1}{s}\int _{-\infty }^{0}f\left( \tau \right) \mathrm {d}\tau \\[ 5pt ]
\hline
\end{array}
\]
2.行列の可制御性
\[
\begin{eqnarray}
\dot {\boldsymbol x} (t) &=&\boldsymbol A\boldsymbol x\left( t\right)+\boldsymbol b u\left( t\right) \\[ 5pt ]
\end{eqnarray}
\]
が与えられているとき,可制御性行列\( \ \boldsymbol U_{\mathrm {c}}=\begin{pmatrix} \boldsymbol b & \boldsymbol A \boldsymbol b \end{pmatrix}\)の行列式\( \ \det \boldsymbol U_{\mathrm {c}}≠0 \ \)の時,可制御となります。例えば,
\[
\begin{eqnarray}
\det \left[ \begin{pmatrix} \boldsymbol b & \boldsymbol A \boldsymbol b \end{pmatrix}\right] &=&\det \begin{bmatrix} 0 & 1 \\ 1 & -4 \end{bmatrix} \\[ 5pt ]
&=&0\times \left( -4\right) -1\times 1 \\[ 5pt ]
&=&-1≠0 \\[ 5pt ]
\end{eqnarray}
\]
の行列は,可制御であると判定できます。
3.行列の可観測性
\[
\begin{eqnarray}
\dot {\boldsymbol x} (t) &=&\boldsymbol A\boldsymbol x\left( t\right)+\boldsymbol b u\left( t\right) \\[ 5pt ]
y(t)&=& \boldsymbol c^{\mathrm {T}} \boldsymbol x (t) \\[ 5pt ]
\end{eqnarray}
\]
が与えられているとき,可観測性行列\( \ \boldsymbol U_{\mathrm {o}}=\begin{pmatrix} \boldsymbol c^{\mathrm {T}} \\ \boldsymbol c^{\mathrm {T}} \boldsymbol A \end{pmatrix}\)の行列式\( \ \det \boldsymbol U_{\mathrm {o}}≠0 \ \)の時,可観測となります。例えば,
\[
\begin{eqnarray}
\det \left[ \begin{pmatrix} \boldsymbol c^{\mathrm {T}} \\ \boldsymbol c^{\mathrm {T}} \boldsymbol A \end{pmatrix}\right] &=&\det \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \\[ 5pt ]
&=&1\times 1 -0\times 0 \\[ 5pt ]
&=&1≠0 \\[ 5pt ]
\end{eqnarray}
\]
の行列は,可観測であると判定できます。
4.行列の安定性
行列の固有値の実数部が正となるものが一つ以上ある場合,実数部が\( \ 0 \ \)となるものが二つ以上ある場合,二対以上の共役な純虚数が存在する場合,不安定となります。
ここで,行列\( \ \boldsymbol A =\begin{pmatrix} a & b \\ c & d \end{pmatrix} \ \)の固有値とは,単位行列\( \ \boldsymbol I =\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \ \)とすると,\( \ \det \left( s\boldsymbol I-\boldsymbol A \right)=0 \ \)の解のことを言います。具体的には,
\[
\begin{eqnarray}
\det \left( s\boldsymbol I-\boldsymbol A \right) &=& 0 \\[ 5pt ]
\left| s\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}-\begin{pmatrix} a & b \\ c & d \end{pmatrix} \right| &=& 0 \\[ 5pt ]
\begin{vmatrix} s-a & -b \\ -c & s-d \end{vmatrix} &=& 0\\[ 5pt ]
\left( s-a \right) \left( s-d \right) -bc &=& 0 \\[ 5pt ]
s^{2}-\left( a+d \right) s+ad-bc &=& 0
\end{eqnarray}
\]
の\( \ s \ \)の解となります。
5.ラウスの安定判別法
特性方程式\( \ a_{0}s^{n}+a_{1}s^{n-1}+a_{2}s^{n-2}+\cdots +a_{n-1}s+a_{n}=0 \ \)が与えられているとき,ラウスの数表は下表にように描くことができ,\( \ 1 \ \)列の値がすべて同符号であるとき,制御系は安定であると判別できます。
\[
\begin{array}{c|ccc}
& \color {red} {1 \ 列} & 2 \ 列 & 3 \ 列 \\
\hline
1 \ 行 & \color {red} {a_{0}} & a_{2} & a_{4} & \cdots \\
2 \ 行 & \color {red} {a_{1}} & a_{3} & a_{5} & \cdots \\
3 \ 行 & \color {red} {b_{1}=\frac {a_{1}a_{2}-a_{0}a_{3}}{a_{1}}} & b_{2}=\frac {a_{1}a_{4}-a_{0}a_{5}}{a_{1}} & \cdots \\
4 \ 行 & \color {red} {c_{1}=\frac {b_{1}a_{3}-a_{1}b_{2}}{b_{1}}} & c_{2}=\frac {b_{1}a_{5}-a_{1}b_{3}}{b_{1}} & \cdots \\
\vdots & \color {red} {\vdots } & \vdots &
\end{array}
\]
6.最終値の定理
\( \ f(t) \ \)のラプラス変換を\( \ F(s) \ \)とすると,\( \ f(t) \ \)の定常値は,
\[
\begin{eqnarray}
\displaystyle \lim _{ t \to \infty } f(t)&=&\displaystyle \lim _{ s \to 0 } sF(s) \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
【解答】
(1)状態空間表現\( \ \left( \boldsymbol A,\boldsymbol b,\boldsymbol c ^{\mathrm {T}}\right) \ \)
\( \ f = 1 \ \)のとき,図1のブロック線図における関係式は,
\[
\begin{eqnarray}
X_{1}\left( s \right) &=&\frac {1}{s-1}U\left( s\right) && \\[ 5pt ]
sX_{1}\left( s \right) – X_{1}\left( s \right) &=&U\left( s\right) && \\[ 5pt ]
sX_{1}\left( s \right) &=& X_{1}\left( s \right) +U\left( s\right) &・・・・・ ①& \\[ 5pt ]
X_{2}\left( s \right) &=&X_{1}\left( s \right) -\frac {5}{s+4}X_{1}\left( s \right) && \\[ 5pt ]
\left( s+4 \right) X_{2}\left( s \right) &=&\left( s+4 \right) X_{1}\left( s \right) -5X_{1}\left( s \right) && \\[ 5pt ]
sX_{2}\left( s \right) +4X_{2}\left( s \right) &=&sX_{1}\left( s \right) -X_{1}\left( s \right) && \\[ 5pt ]
sX_{2}\left( s \right) &=&-4X_{2}\left( s \right) +X_{1}\left( s \right) +U\left( s\right) -X_{1}\left( s \right) &\left( ∵①を代入\right)& \\[ 5pt ]
&=&-4X_{2}\left( s \right) +U\left( s\right) &・・・・・ ②& \\[ 5pt ]
\end{eqnarray}
\]
となるので,①式及び②式を逆ラプラス変換すると,
\[
\begin{eqnarray}
\frac {\mathrm {d}x_{1}\left( t \right) }{\mathrm {d}t} &=& x_{1}\left( t \right) +u\left( t \right) &・・・・・・・・・ ①^{\prime }& \\[ 5pt ]
\frac {\mathrm {d}x_{2}\left( t \right) }{\mathrm {d}t}&=&-4x_{2}\left( t \right) +u\left( t \right) &・・・・・・・・・ ②^{\prime }& \\[ 5pt ]
\end{eqnarray}
\]
となり,これを行列の形にすれば,
\[
\begin{eqnarray}
\frac {\mathrm {d}}{\mathrm {d}t}\begin{bmatrix}
x_{1}\left( t \right) \\
x_{2}\left( t \right)
\end{bmatrix} &=& \begin{bmatrix}
1 & 0 \\
0 & -4
\end{bmatrix} \begin{bmatrix}
x_{1}\left( t \right) \\
x_{2}\left( t \right)
\end{bmatrix} +\begin{bmatrix}
1 \\
1
\end{bmatrix} u \left( t \right) \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ \displaystyle \boldsymbol A=\begin{bmatrix}
1 & 0 \\
0 & -4
\end{bmatrix} \ \),\( \ \displaystyle \boldsymbol b=\begin{bmatrix}
1 \\
1
\end{bmatrix} \ \)
と求められる。また,図1において,
\[
\begin{eqnarray}
Y\left( s \right) &=&X_{2}\left( s\right) \\[ 5pt ]
\end{eqnarray}
\]
となるので,これを逆ラプラス変換すると,
\[
\begin{eqnarray}
y\left( t \right) &=&x_{2}\left( t\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,行列の形にすれば,
\[
\begin{eqnarray}
y\left( t \right) &=&\begin{bmatrix}
0 & 1
\end{bmatrix}\begin{bmatrix}
x_{1}\left( t \right) \\
x_{2}\left( t \right)
\end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ \displaystyle \boldsymbol c ^{\mathrm {T}}=\begin{bmatrix}
0 & 1
\end{bmatrix} \ \)と求められる。
(2)状態空間表現の可制御性,可観測性及び\( \ u\left( t\right) =0 \ \)のときの原点\( \ \displaystyle \boldsymbol x =\begin{bmatrix}
0 \\
0
\end{bmatrix} \ \)の周りの安定性
可制御性判別のため,ワンポイント解説「2.行列の可制御性」に沿って\( \ \boldsymbol A \boldsymbol b \ \)を求めると,
\[
\begin{eqnarray}
\boldsymbol A \boldsymbol b &=&\begin{bmatrix}
1 & 0 \\
0 & -4
\end{bmatrix}\begin{bmatrix}
1 \\
1
\end{bmatrix} \\[ 5pt ]
&=&\begin{bmatrix}
1 \\
-4
\end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
であるため,可制御性行列\( \ \boldsymbol U_{\mathrm {c}}=\begin{pmatrix} \boldsymbol b & \boldsymbol A \boldsymbol b \end{pmatrix} \ \)の行列式\( \ \det \boldsymbol U_{\mathrm {c}} \ \)は,
\[
\begin{eqnarray}
\det \left[ \begin{pmatrix} \boldsymbol b & \boldsymbol A \boldsymbol b \end{pmatrix}\right] &=&\det \begin{bmatrix} 1 & 1 \\ 1 & -4 \end{bmatrix} \\[ 5pt ]
&=&-4-1 \\[ 5pt ]
&=&-5≠0 \\[ 5pt ]
\end{eqnarray}
\]
となり,可制御であることがわかる。
次に可観測性判別のため,ワンポイント解説「3.行列の可観測性」に沿って\( \ \boldsymbol c^{\mathrm {T}} \boldsymbol A \ \)を求めると,
\[
\begin{eqnarray}
\boldsymbol c^{\mathrm {T}} \boldsymbol A &=&\begin{bmatrix}
0 & 1
\end{bmatrix}\begin{bmatrix}
1 & 0 \\
0 & -4
\end{bmatrix} \\[ 5pt ]
&=&\begin{bmatrix}
0 & -4
\end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
であるため,可観測性行列\( \ \boldsymbol U_{\mathrm {o}}=\begin{pmatrix} \boldsymbol c^{\mathrm {T}} \\ \boldsymbol c^{\mathrm {T}} \boldsymbol A \end{pmatrix}\)の行列式\( \ \det \boldsymbol U_{\mathrm {o}} \ \)は,
\[
\begin{eqnarray}
\det \left[ \begin{pmatrix} \boldsymbol c^{\mathrm {T}} \\ \boldsymbol c^{\mathrm {T}} \boldsymbol A \end{pmatrix}\right] &=&\det \begin{bmatrix} 0 & 1 \\ 0 & -4 \end{bmatrix} \\[ 5pt ]
&=&0-0 \\[ 5pt ]
&=&0 \\[ 5pt ]
\end{eqnarray}
\]
となり,可観測でないことがわかる。
さらに安定性判別のため,ワンポイント解説「4.行列の安定性」に沿って\( \ s\boldsymbol I-\boldsymbol A \ \)を求めると,
\[
\begin{eqnarray}
s\boldsymbol I-\boldsymbol A &=&s \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}-\begin{bmatrix}1 & 0 \\ 0 & -4\end{bmatrix} \\[ 5pt ]
&=&\begin{bmatrix}s-1 & 0 \\ 0 & s+4\end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
となり,固有値を求めると,
\[
\begin{eqnarray}
\det \left( s\boldsymbol I-\boldsymbol A\right) &=&0 \\[ 5pt ]
\det \begin{bmatrix}s-1 & 0 \\ 0 & s+4\end{bmatrix} &=&0 \\[ 5pt ]
\left( s-1\right) \left( s+4\right) &=&0 \\[ 5pt ]
s&=&1,-4 \\[ 5pt ]
\end{eqnarray}
\]
となり,固有値の実数部が正となる解があるので,このシステムは不安定であることがわかる。
(3)図2のフィードバック制御系が安定となるための\( \ K \ \)の範囲
図2における\( \ R \left( s\right) \ \)から\( \ Y \left( s\right) \ \)までの伝達関数は,
\[
\begin{eqnarray}
K\left( 1+\frac {2}{s}\right) E \left( s\right) &=&U \left( s\right) &・・・・・・・・・・ ③& \\[ 5pt ]
\frac {1}{s-1}U \left( s\right)\cdot 3-\frac {1}{s-1}U \left( s\right) \cdot \frac {5}{s+4} &=&Y \left( s\right) \\[ 5pt ]
3\left( s+4\right) U \left( s\right)-5U \left( s\right) &=&\left( s-1\right) \left( s+4\right) Y\left( s\right) \\[ 5pt ]
\left( 3s+7\right) U \left( s\right) &=&\left( s^{2}+3s-4\right) Y\left( s\right) \\[ 5pt ]
Y\left( s\right) &=&\frac {3s+7}{s^{2}+3s-4} U \left( s\right) \\[ 5pt ]
&=&\frac {3s+7}{s^{2}+3s-4}\cdot K\left( 1+\frac {2}{s}\right) E \left( s\right) \left( ∵③を代入\right) \\[ 5pt ]
&=&\frac {3Ks^{2}+13Ks+14K}{s^{3}+3s^{2}-4s} \left\{ R \left( s\right) -Y \left( s\right)\right\} \\[ 5pt ]
Y\left( s\right) +\frac {3Ks^{2}+13Ks+14K}{s^{3}+3s^{2}-4s}Y\left( s\right) &=&\frac {3Ks^{2}+13Ks+14K}{s^{3}+3s^{2}-4s} R \left( s\right) \\[ 5pt ]
\frac {s^{3}+\left( 3K+3\right) s^{2}+\left( 13K-4\right) s+14K}{s^{3}+3s^{2}-4s}Y\left( s\right) &=&\frac {3Ks^{2}+13Ks+14K}{s^{3}+3s^{2}-4s} R \left( s\right) \\[ 5pt ]
\left\{ s^{3}+\left( 3K+3\right) s^{2}+\left( 13K-4\right) s+14K\right\} Y\left( s\right) &=&\left( 3Ks^{2}+13Ks+14K\right) R \left( s\right) \\[ 5pt ]
\frac {Y\left( s\right) }{R \left( s\right) }&=&\frac {3Ks^{2}+13Ks+14K}{s^{3}+\left( 3K+3\right) s^{2}+\left( 13K-4\right) s+14K} &・・・・・・・・・・ ④& \\[ 5pt ]
\end{eqnarray}
\]
となるので,特性方程式\( \ s^{3}+\left( 3K+3\right) s^{2}+\left( 13K-4\right) s+14K=0 \ \)についてラウス表を作成すると,ワンポイント解説「5.ラウスの安定判別法」の通り,
\[
\begin{array}{c|cc}
& 1列 & 2列 \\
\hline
1行 & 1 & 13K-4 \\
2行 & 3K+3 & 14K \\
3行 & \frac {\left( 3K+3\right) \left( 13K-4\right) -14K}{3K+3} & 0 \\
4行 & 14K & \\
\end{array}
\]
となるので,安定となる条件は,\( \ 3 \ \)行\( \ 1 \ \)列の式より,
\[
\begin{eqnarray}
\frac {\left( 3K+3\right) \left( 13K-4\right) -14K}{3K+3}&>&0 \\[ 5pt ]
\left( 3K+3\right) \left( 13K-4\right) -14K&>&0 \\[ 5pt ]
39K^{2}+13K -12&>&0 \\[ 5pt ]
K&<&\frac {-13-\sqrt {13^{2}+4\times 39\times 12 }}{78},K>\frac {-13+\sqrt {13^{2}+4\times 39\times 12 }}{78} \\[ 5pt ]
K&<&\frac {-13-\sqrt {2041}}{78},K>\frac {-13+\sqrt {2041}}{78} \\[ 5pt ]
\end{eqnarray}
\]
となり,その他\( \ 14K >0 \ \)より\( \ \displaystyle K>0 \ \)の条件があるので,制御系が安定となる条件は\( \ \displaystyle K>\frac {-13+\sqrt {2041}}{78} \ \)と求められる。
(4)図2のフィードバック制御系が安定であるとき,目標値\( \ r\left( t\right) =t \ \)に対する定常偏差
図2より,\( \ R\left( s \right) -Y\left( s \right) =E\left( s \right) \ \)であり,これに④式を代入すると,
\[
\begin{eqnarray}
R\left( s \right) -\frac {3Ks^{2}+13Ks+14K}{s^{3}+\left( 3K+3\right) s^{2}+\left( 13K-4\right) s+14K}R\left( s \right) &=&E\left( s \right) \\[ 5pt ]
\frac {s^{3}+3 s^{2}-4s}{s^{3}+\left( 3K+3\right) s^{2}+\left( 13K-4\right) s+14K}R\left( s \right) &=&E\left( s \right) \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ r\left( t\right) =t \ \)のラプラス変換は\( \ \displaystyle R\left( s\right) =\frac {1}{s^{2}} \ \)であるから,定常偏差は,ワンポイント解説「6.最終値の定理」の通り,
\[
\begin{eqnarray}
\displaystyle \lim _{ t \to \infty } e(t)&=&\displaystyle \lim _{ s \to 0 } sE(s) \\[ 5pt ]
&=&\displaystyle \lim _{ s \to 0 } \left\{ s\cdot \frac {s^{3}+3 s^{2}-4s}{s^{3}+\left( 3K+3\right) s^{2}+\left( 13K-4\right) s+14K}R\left( s \right) \right\} \\[ 5pt ]
&=&\displaystyle \lim _{ s \to 0 } \left\{ s\cdot \frac {s^{3}+3 s^{2}-4s}{s^{3}+\left( 3K+3\right) s^{2}+\left( 13K-4\right) s+14K}\cdot \frac {1}{s^{2}} \right\} \\[ 5pt ]
&=&\displaystyle \lim _{ s \to 0 } \left\{ \frac {s^{2}+3 s-4}{s^{3}+\left( 3K+3\right) s^{2}+\left( 13K-4\right) s+14K} \right\} \\[ 5pt ]
&=&\frac {-4}{14K} \\[ 5pt ]
&=&-\frac {2}{7K} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん